Correcting Springback

Springback

• Correcting Springback: Overview
• Correcting Springback by Changing the Elastic Stress Distribution: Post Stretch (Stake Beads)
• Correcting Springback by Changing the Elastic Stress Distribution: Over-Forming
• Correcting Springback by Reducing or Minimizing the Elastic Stresses
• Correcting Springback by Locking in the Elastic Stresses
• Tooling Design and Stamping Process Contributions to Springback
• Case Studies in Springback Reduction Strategies
• Key Points

Overview

Forming a part at room temperature creates elastic stresses, which will require some form of springback correction to bring the stamping back to part print. Forming at sufficiently high temperatures, such as with press hardening steels, allows for stress relief before the part leaves the die.

Springback correction can take many forms. The first approach is to apply an additional process that changes the elastic stresses to a less damaging form. One example is a post-stretch operation that reduces sidewall curl by changing the tensile-to-compressive elastic stress gradient through the thickness of the sidewall to all tensile elastic stresses though the thickness. Another example is over-forming panels and channels so that the release of elastic stresses brings the part dimensions back to part print instead of becoming undersized.

A second approach is to modify the process and/or tooling to reduce the level of elastic stresses created during the forming operation. An example is to reduce sidewall curl by replacing sheet metal flowing through draw beads and over a die radius with a simple 90 degree bending operation.

A third approach for correcting springback problems is to modify product design to resist the release of the elastic stresses. Here, mechanical stiffeners added to the part design lock in the elastic stresses and maintain desired part shape.

The approaches to springback correction described below are applicable to all higher strength steels, and typically will address both angular change and sidewall curl. AHSS grades having high flow stress in the formed part may require one or more of these approaches for satisfactory dimensional accuracy.

Minimizing springback through compensation in the first draw stage is more effective and less expensive than attempting to correct for existing springback in subsequent re-strike or re-forming operations. Approaches for improved dimensional accuracy include:

• Minimizing bending/unbending as the metal flows to the final part shape reduces distortion and tool wear.
• Reaching minimum strain levels across the panel minimizes springback and sidewall curl.
• Accounting for tool material loss during recuts helps ensure sufficient tool stiffness to counteract the higher press forces required with AHSS grades.
• Keeping the depth of AHSS channel-shaped parts as uniform as possible avoids forming distortions. Gradual shape transitions will minimize distortions, especially in areas of metal compression. Designing radii so there are only gradual transitions avoids stress risers and minimizes distortions. Minimize stretch/compression flanges wherever possible.
• If die and process design cannot relieve all elastic stresses, then creating a uniformly distributed residual stress pattern across the sheet and through the thickness will help eliminate the source of mechanical multiplier effects and thus lead to reduced springback problems.

Correcting Springback by Changing the Elastic Stress Distribution: Post-Stretch (Stake Beads, Hybrid Beads, and Active Binder Force Control)

One of the most effective techniques for significant reduction of both angular change and sidewall curl is a post-stretch operation. Applying an in-plane tensile force after all operations in which the sheet metal is bent and unbend over draw beads and across die radii can change the through-thickness tensile-to-compressive elastic stress gradients to all tensile elastic stresses.

When the part is still in the die, the outer surface of the bend over the punch radius is in tension (Point A in Figure 1), while at the same time the inner surface is in compression (B). After the punch retracts and the part is no longer under load, the tensile elastic stresses (A) tend to shrink the outer layers and the compressive elastic forces (B) tend to elongate the inner layers. These opposite forces form a mechanical advantage to magnify the angular change. The differential stress ∆σ is the driver for the dimensional change. Note that this reversal in stress direction after removal of the applied load is the same root cause that results in snap-through reverse tonnage reactions when punching higher strength steels.

Figure 1: Sheet metal bent over a punch radius has elastic stresses of the opposite sign creating a mechanical advantage to magnify angular change. Similar effects create sidewall curl for sheet metal pulled through draw beads and over die radii. When the part is no longer under load, it will change shape to relieve these elastic stresses.

In the case of side wall curl, this differential stress ∆σ increases as the sheet metal is work hardened going through draw beads and around the die radius into the wall of the part.

To correct this angular change and sidewall curl, apply a tensile stress to the flange end of the wall to generate a minimum tensile strain of 2% within the sidewall of the stamping. Figure 2 describes the sequence of events. The initial elastic states are tensile (A1) and compressive (B1). When approximately 2% tensile strain is added to A1, the strain point work hardens and moves up slightly to A2. However, when 2% tensile strain is added to B1, the compressive elastic stress state first decreases to zero, then climbs to a positive level and work hardens slightly to point B2. The neutral axis is moved out of the sheet metal. The stress differential ∆σ now approaches zero. Instead of bending or curving outward, the wall simply shortens by a small amount similar to releasing the load on a tensile test sample. This shortening of the wall length can be easily corrected by an increased punch stroke.

Figure 2: The large stress differential shown in Figure 1 is significantly reduced by applying a 2% tensile strain.

Post-Stretch with Stake Beads

Two die design methods currently in use can create the desired minimum 2% post-stretch on the sidewall of AHSS parts, both of which utilize what are commonly referred to as stake beads.

The first method involves retractable beads located in machined slots in the lower blankholder. The upper blankholder has machined stake bead pockets. Adjustable stop blocks located directly under the retractable stake beads can be shimmed to alter the timing when the stake bead engages the stamping, if required.

At the targeted punch stroke position, the retractable beads hit the stop blocks which forces them into the sheet metal flange. This creates a blank locking action while the punch continues to deform the part. As the die opens, the stake beads retract, and the cycle repeats itself from press stroke to press stroke. Adjustability of the draw bead height has advantages, particularly during initial die tryout.

As the retractable beads are inserts, removing them for hardening, coating, polishing, etc., is much easier than moving an entire die to perform bead work. Duplicate inserts can also be made, even utilizing alternative tool steels to increase durability. Locating the retractable stake bead on the blankholder, however, can lead to a larger required blank size. Die construction costs for retractable stake beads are also higher due to the additional machining required.

It is important to have adequate structural die support to avoid breaking the die. Significantly greater lateral thrust forces can cause catastrophic die failure if the stake beads are located too close to the punch opening. This is also true for many other die components, so die construction standards for mild and HSLA steels may not apply to AHSS.

An alternate approach is to locate the stake beads on the punch. Stake beads are machined directly in the punch casting, with the stake bead pockets machined into the upper die cavity. This approach may allow for a reduced blank size, since less material is needed outside the punch opening to accommodate both the draw bead and the stake bead. Figure 3 shows a DP590 B-pillar draw panel with draw beads located on the blankholder and stake beads located on the punch just inboard of the draw beads.

Figure 3: DP590 B-pillar with draw beads on the blankholder and stake beads on the punch. Yellow arrows point to the stake beads; blue arrows point to the draw beads located closer to the edge of the draw panel.

Figure 4 shows a draw die punch with stake beads machined at the very edge of the punch opening, along with the upper die with the stake bead pockets machined out.

Figure 4: Left Image – Stake beads machined into the punch of this DP780 die; Right Image: Stake bead pockets machined into the upper draw die. Note that there are no draw beads on this blankholder.

Draw beads control metal flow in draw dies. However, draw beads may become less functional when forming higher strength sheet steels having higher work hardening characteristics. Here, bending and straightening when pulling the sheet through the punch opening radius, combined with bearing on the binder surface, may be sufficient to control metal flow.

The punch and upper binder in Figure 4 have no draw beads, and instead exhibit stake beads that engage late in the press stroke. This solution is lower in cost but provides limited flexibility since the beads are machined directly into the die. In contrast, Figure 5 shows a die with removable stake bead inserts located on the punch. This approach has improved adjustability, but the added expense of machining the die and installing stake bead inserts.

Figure 5: This die has adjustable stake beads located on the punch as inserts, and do not retract during every press stroke. Note also that there are no draw beads on the blankholder.^A-6

A third option to achieve the post forming 2% strain on the part with stake beads involves an additional die or die station. After nearly fully forming the part in the first die, a second die locks the remaining flange in place and further deforms the part by the additional 2%. This approach is expensive since it requires construction of an additional die, or if processed in a progressive die, adding this extra station increases the size and complexity of the progressive die.

Ensuring dimensional precision may require a restrike operation after trimming. In addition to sharpening the radii, the restrike die may provide the sidewall stretch (post-stretch) of approximately 2% required to eliminate curl.

Studies have shown that the height and geometry of the stake bead can impact springback control. Insufficient stretching below the targeted 2% post-stretch may not sufficiently address springback. If the restraining force of the stake bead is too great, it could lead to fracture at the bead or punch opening radius.

Adjusting the stake bead geometry around the part creates an unbalanced post-stretching configuration. Researchers applied this approach to counteract springback in a 3rd Generation steel, with more shallow beads used on deeper drawn sections of the tested part.^J-11

The magnitude of springback is a function of the uniformity of the stress distribution through the thickness direction the wall of the formed sheet. An optimized combination of draw beads and stake beads promotes a uniform stress distribution through the thickness, which leads to improved springback control (Figures 6 and 9). Successful simulation provides a range of acceptable combinations of draw bead and stake bead heights.^Z-15

Figure 6:  A combination of draw beads and stake beads promote a uniform stress distribution through the thickness, leading to improved springback control.^Z-15

Press Force and Energy Considerations when using Stake Beads

These post-stretch forming operations normally require significantly higher forming forces and energy requirements to be effective for several reasons.

Any sheet metal will work harden after going through draw beads. Since AHSS grades work harden to a greater degree than conventional high strength steels, the AHSS grades have significantly higher yield strength once the blank has passed over the draw beads. As stake beads are located inboard of draw beads, the stake bead must now deform material with a much higher yield strength due to the work hardening created by the bending and straightening of the material from being pulled through the draw bead.

Since stake beads engage late in the press stroke, their use has similar implications as creating embossments as discussed in a Press Energy case study in the Press Requirements page. This Case Study^H-3 shows that the last increment of punch travel required to finish embossing requires significantly higher energy for AHSS versus conventional mild or HSLA steel. In the current discussion on stake beads, inducing an additional 2% post forming strain into the part will also require higher forming forces and energy requirements, since the forming process work hardened and strengthened the sidewalls. Even if the press has sufficient force and energy characteristics, avoid necking down and tearing the sheet metal as it bends over the punch radius.

Case Studies: Using Stake Beads to Reduce Springback ^L-1

This case study evaluated springback on specially constructed dies tested using several grades of conventional and advanced high strength steels, including HSLA, dual phase, and TRIP grades with tensile strength ranging from 450 MPa to 980 MPa. One die used the conventional approach, allowing for metal to flow from the flange without a bead. The second die had a recessed square stake bead in the flange that created a post-stretch condition near the end of the stroke. As expected, the post-stretch die resulted in dramatically lower springback (Figure 7). In addition, springback on parts made with this die was not a function of the sheet metal tensile strength, making for a more robust process.

Figure 7: Comparison of two DP 450/750 parts, where stake beads in the bottom part minimized springback. Both images are different angles of the same parts.^L-1

Post-Stretch with Hybrid Beads

As seen in the prior figures, the stake beads geometry plays an important role in restricting the metal flow when stretching the sidewalls during the last stages of the punch stroke. This approach requires a larger blank to accommodate the bead, and must be used in a press with sufficient tonnage to set the bead.

A modified approach significantly reduces the blank size requirements as well as lowers the required tonnages to create the bead. It uses stinger beads to penetrate the sheet metal as well as create a wave shape in the deformed region which restricts metal flow. This so-called hybrid bead takes up less than 25% of the bead surface area compared with a conventional stake bead, allowing for a measurably smaller blank. There is no bending over tight bead radii, eliminating the splitting risk at the bead. The restricted metal motion across the beads further minimizes the stress differential between the two sheet steel surfaces, which eliminates a significant root cause of sidewall curl.

Figure 8 highlights the influence a hybrid bead has on springback of a 3rd Generation Steel having a minimum tensile strength of 980MPa.

Figure 8: Hybrid bead dramatically reduces springback in a 3^rd Generation steel having 980 MPa minimum tensile strength, while taking up less space and requiring reduced tonnage than stake beads.^A-6

Animations of the process sequence is presented in Figures 9 and 10, with more information available in Citations J-12 and W-19.

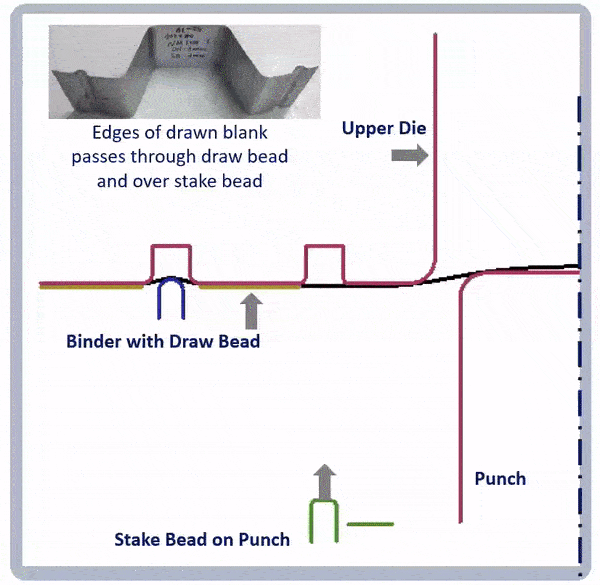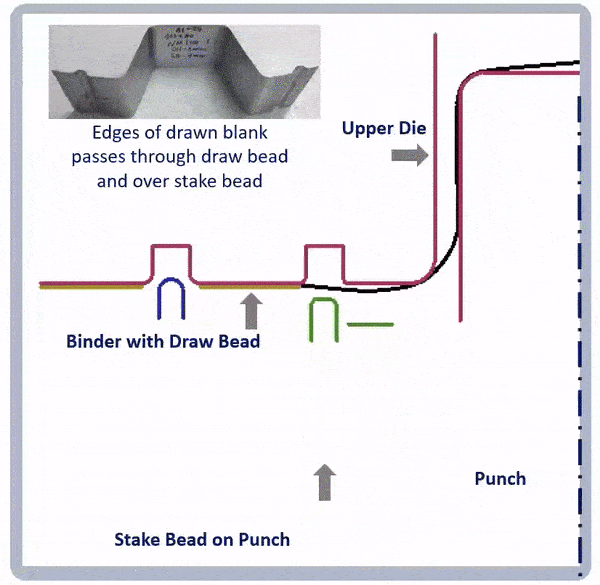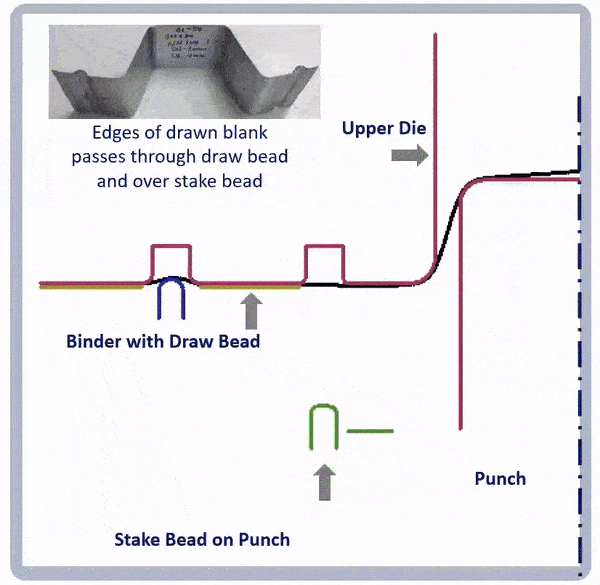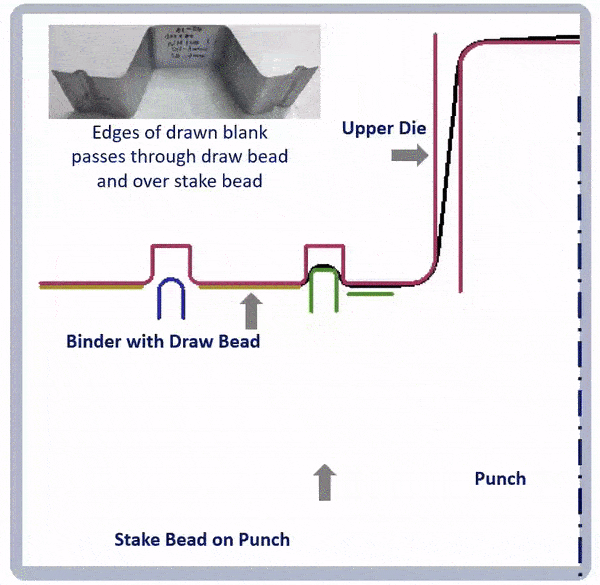
Figure 9: Animation showing a combination of draw beads and stake beads to reduce springback.^A-6

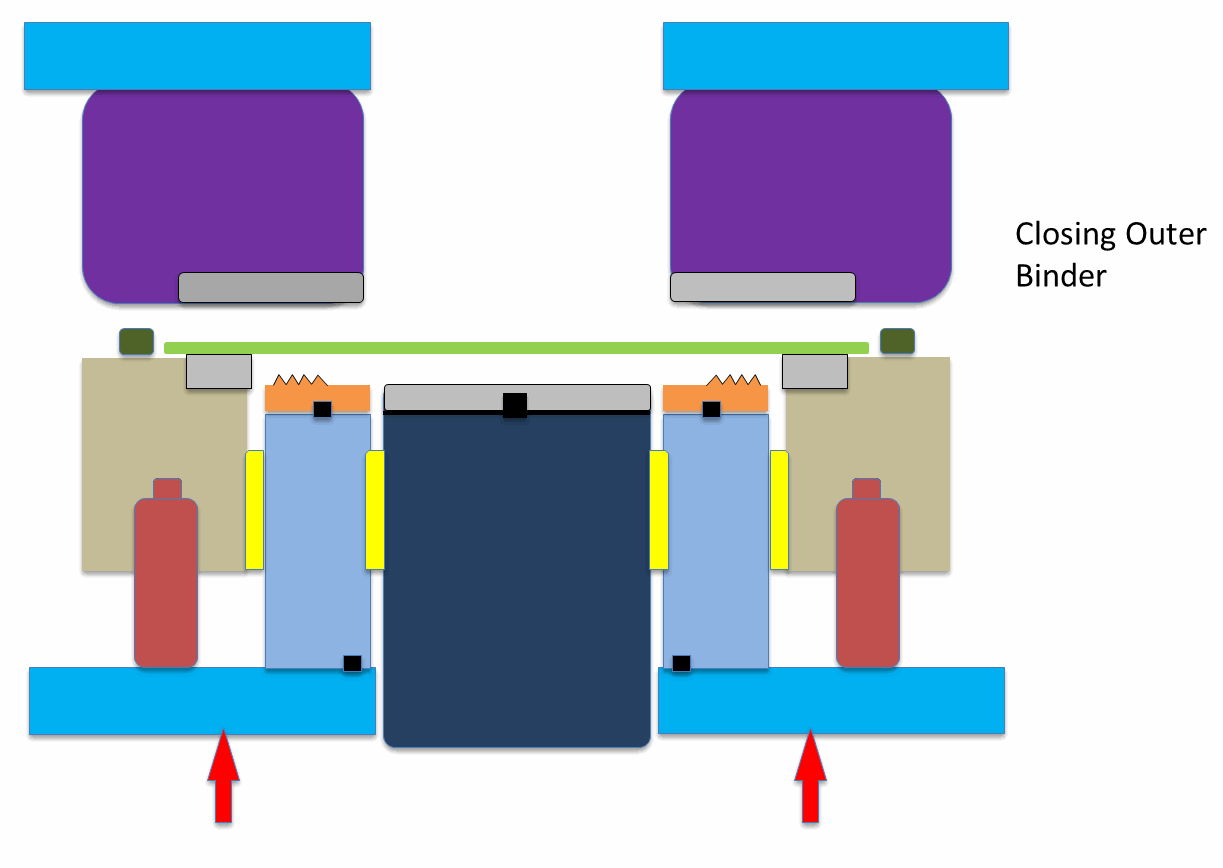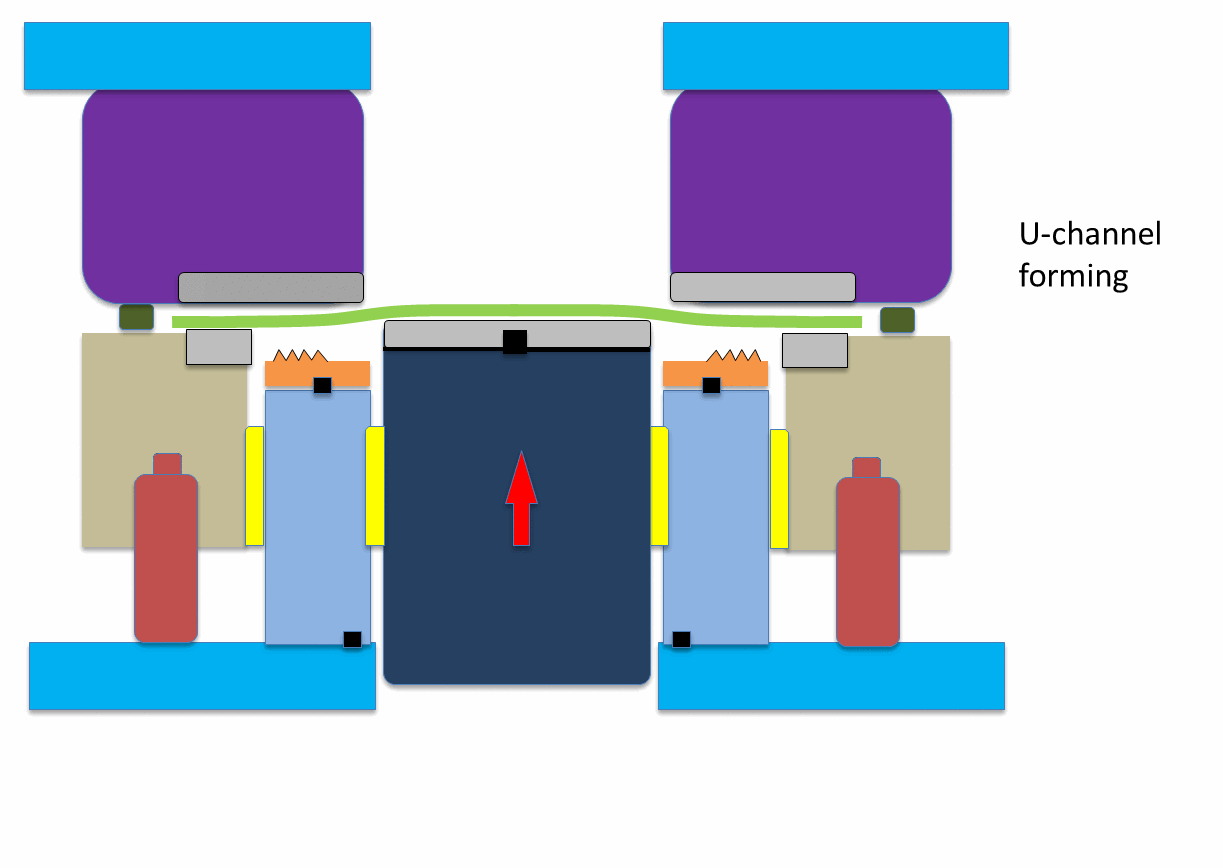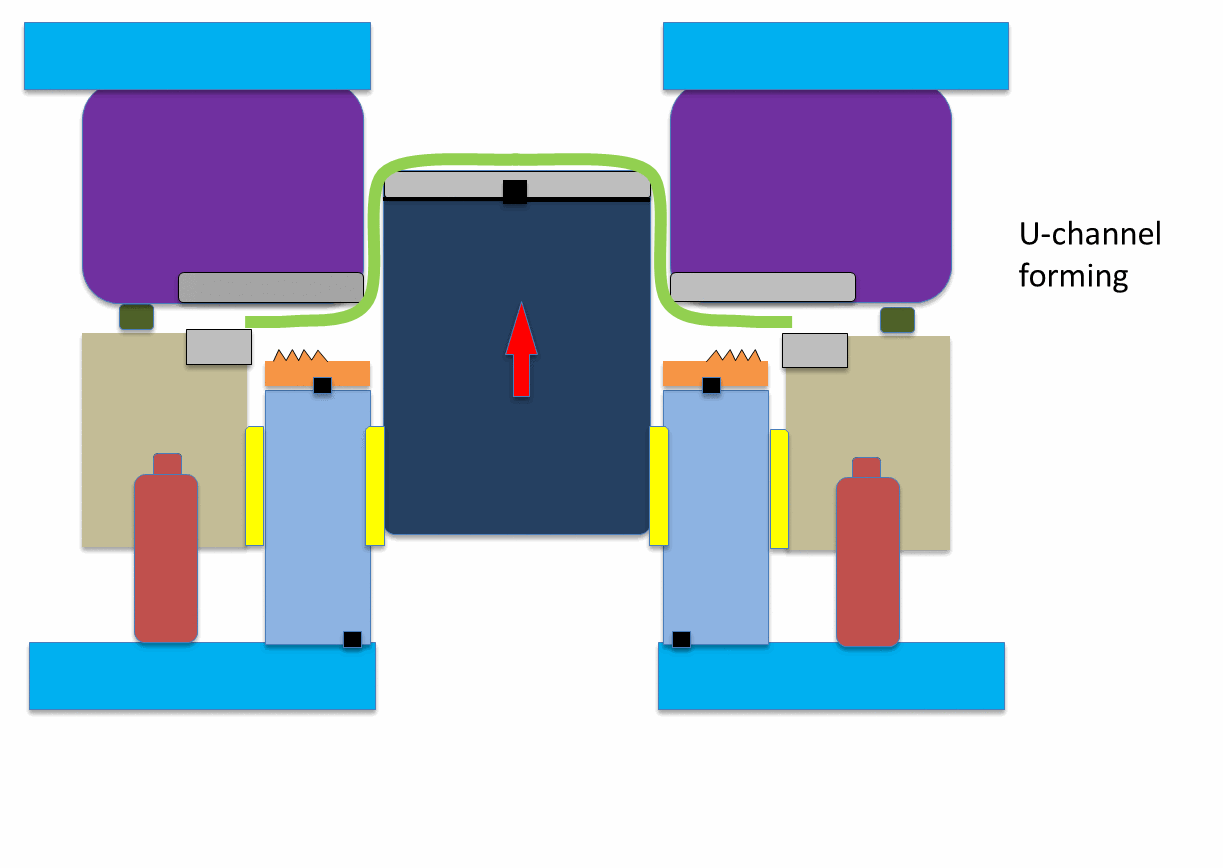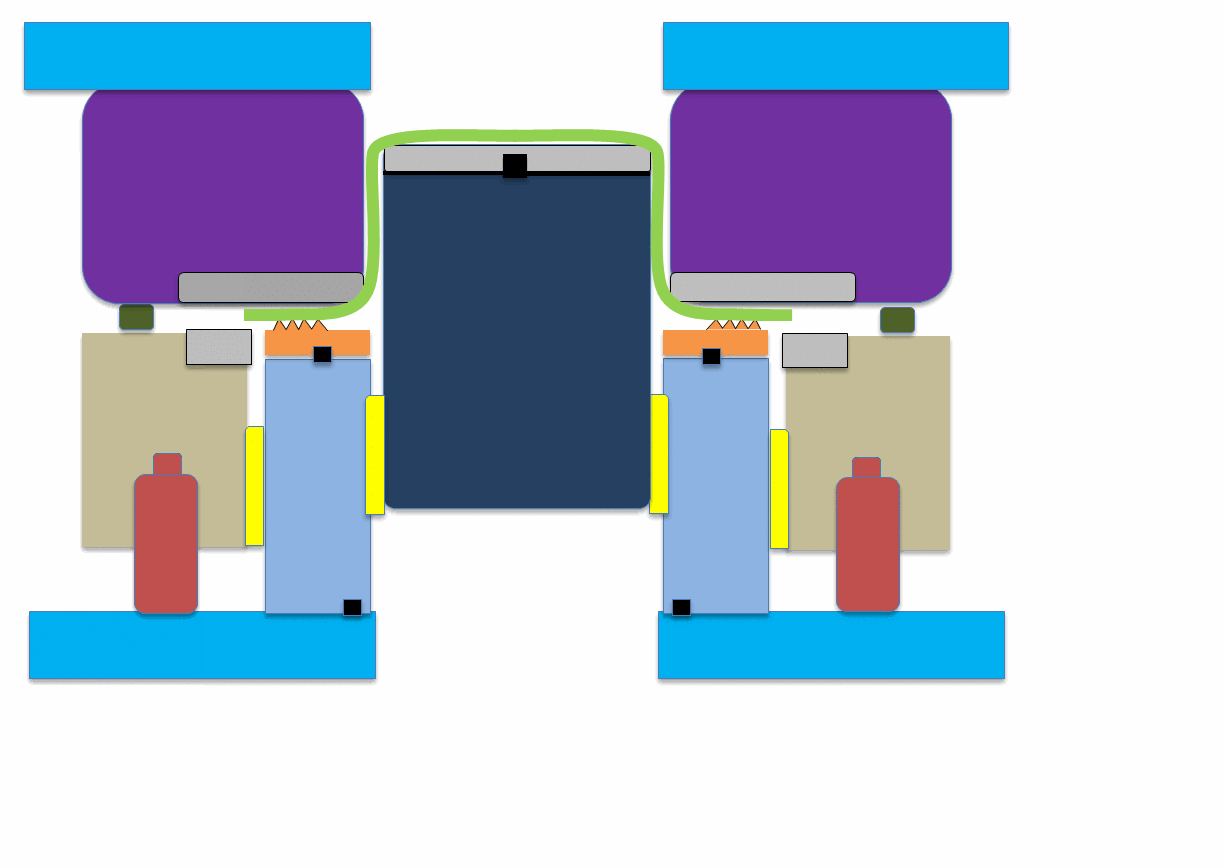
Figure 10: Animation showing application of hybrid beads to reduce springback.^A-6

Post-Stretch with Active Binder Force Control

While most stamping processes apply binder pressure uniformly throughout the press stroke, modern stamping presses can be equipped with cushions having multipoint-control systems. Adjusting the associated pressure profile around the panel and throughout the stroke optimizes metal flow, prevent splits and wrinkles, and minimize thinning. This active binder force control capability allows for application of increased blank holder force at any point of the stroke, including at the end to achieve the targeted 2% post-stretch needed to minimize springback. (See the AHSS Insights blog by Dr. Daniel Schaeffler from Engineering Quality Solutions, Inc.)

Beyond simply increasing the blank holder force at the end of the stroke, varying the pressure sequence during the stroke may be beneficial as well. DP 340/590 steel was stamped using a constant binder force, an increasing binder force starting low and finishing high, and a third approach where the initial part of the stroke formed the part with a medium binder force which dropped for most of the stroke but increased at the end to apply the sidewall tension. This third approach resulted in the least angular change and sidewall curl, as seen in Figure 11.

Figure 11: DP 340/590 stamped with constant binder force (top), low-to-high binder force (middle), and medium-to-low-to-high binder force (bottom).^P-14

Correcting Springback by Changing the Elastic Stress Distribution: Over-Forming

Many angular change problems initiate when constructing the tooling either to part print or without sufficient springback compensation. Achieving targeted dimensions may require over-forming or over-bending.

Use rotary bending tooling where possible instead of flange wipe dies. Rotary bending allows for easy adjustment of the bending angle to correct for changes in springback due to variations in steel properties, die set, lubrication, and other process parameters. In addition, the tensile loading generated by the wiping shoe is absent.

However, if over-bending with flange wipe dies is the chosen approach to minimize angular change, use die radii less than the part radius and use back relief for the die and punch (Figure 12). This approach intentionally subjects the bending radius to compressive stresses between the punch and die. The squeezing and associated thinning at the bend radius results in plastic deformation of the sheet steel, with little elastic recovery after unloading from the press.

Figure 12: Providing back relief on the flange steel and lower die aids over-bending.^A-2

Cross section design for longitudinal rails, pillars, and cross members impacts the effectiveness of springback compensation methods. The rail cross section in sketch A of Figure 13 does not allow the use of over-bending for springback compensation in the forming die. In addition, this design likely leads to severe sidewall curl in AHSS channel-shaped cross sections. Minimize these quality issues by designing a cross section that allows for over-bending during forming, as shown in sketch B. Reduced sidewall curl is another benefit of this cross-sectional design. Springback allowance must increase as strength increases. Typical wall opening angles are 3-degrees for Mild steel, 6 degrees for DP 350/600 and 10 degrees for DP 850/1000 or TRIP 450/800. In addition, the cross section in sketch B will have the effect of reducing the impact shock load when the draw punch contacts the AHSS sheet. The vertical draw walls shown in sketch A require higher binder pressures and higher punch forces to maintain process control.

Figure 13: Changing a rail cross section from A to B allows easier over-bending for springback control.^N-3

Producing closed box sections involves welding two channel sections together at their flanges. Hat-sections with 90-degree corners such as seen in sketch A of Figure 14 will experience many production problems since each component will have issues with sidewall curl and angular change. The hexagonal section in sketch B will reduce sidewall curl and twist problems, while permitting over-bend for springback compensation in the stamping dies.

Figure 14: Changing the design of a closed cross section from A to B leads to a reduction in springback problems.^N-3

Adding extra stages to the forming process allows for secondary operations to return a sprung part back to nominal dimensions. For example, Figure 15 shows a process where a crown existing in the first step when forming a channel section uses a second die for flattening and eliminating sidewall springback.

Figure 15: Schematic showing how flattening a crown corrects angular springback.^A-3

As a related process, multiple stage forming (Figure 16) is an option to minimize springback and improve dimensional accuracy when stamping rails or other parts with a hat-shaped cross section consisting of right angles. This processing approach creates a design which avoids re-working previously-formed (and therefore work hardened) sections.

In the first operation, all 90-degree radii and mating surfaces are formed using “gull-wing” processes with over bending to compensate for springback. The larger radius in the top of the hat section gets flattened in the second stage. Certain cases may require an over bending of the flat top section.

Multiple-stage forming also helps when forming parts having small geometrical features of severe geometry that can be formed only in the re-strike operation. A part that has a variable cross section in combination with small geometrical features may need a coining operation in the second or last stage of the forming process. This may be the only way to control the geometry.

Figure 16:  Two-stage forming produces a dimensionally accurate hat section with relatively small radii.^R-1

Correcting Springback by Reducing or Minimizing the Elastic Stresses

The process design, and therefore the tooling design, can drastically affect the level of the elastic stresses in the part.

As an example, different blankholder actions provide four possible processes to form a hat-profile channel, each with different dimensional accuracy (Figure 17). The four processes are:

• Draw: the conventional forming type with continuous blankholder force and all blank material undergoing maximum bending and unbending over the die radius. This forming mode creates maximum sidewall curl.
• Form-draw: a forming process in which application of the blank holder force occurs between the middle and last stage of forming. It is most effective to reduce the sidewall curl because this approach minimizes bend unbend deformation at the beginning of the stroke prior to application of any blank holder force. Applying a large tensile stress during the last stage of forming creates the post-stretch condition to further minimize curl.
• Form: a process where the flange is created during in the last stage of forming and the material undergoes only a slight amount of bend-unbend deformation. Depending on the part geometry, the lack of a blankholder may lead to wrinkles.
• Bend is a simple bending process to reduce the sidewall curl, which avoids the bend and unbend sequence associated with sidewall curl. However, this approach likely leads to an angular change in the sidewall.

Figure 17: Four processes for generating a channel for bumper reinforcement create different levels of elastic stress and springback.^K-5

Correcting Springback by Locking in the Elastic Stresses

Where part design allows, geometrical features like darts, beads, and stiffeners prevent the release of the elastic stresses and reduce various forms of springback. Minimize twist by adding strategically placed vertical beads, darts, or other geometric stiffeners in the shorter length wall to equalize the length of line.

Applying these features in a restrike operation may not be possible due to equipment or design limitations, since the yield strength of the sheet metal increases after work hardening. In the case of AHSS grades, this work hardening leads to a dramatic increase in strength.

Any elastic stress locked into the panel remains in the part as residual or trapped stresses. Subsequent forming, trimming, punching, heating, or other processes may unbalance the residual stress and change the part shape. For these reasons, the full process needs to be simulated, incorporating both material and geometrical changes occurring in all prior operations.

Figures 18 to 22 present examples of how elastic stresses can be locked into the part to control for springback.

Figure 18: Geometrical stiffeners like flanges or beads lock elastic stresses into the part, fixing the part shape.^A-2

Figure 19: B-pillar using stiffening darts to control springback.^A-41

Figure 20: Step flange locks in elastic stresses on a draw wall.^A-41

Figure 21: Hat section showing the effects geometrical features have on controlling springback. Angular change and sidewall curl are noticeably less pronounced on the left side having the vertical beads, compared with the right side where no springback mitigation methods were employed.^K-14

Figure 22: DP600 front rail upper reinforcement with vertical beads designed into the part geometry for springback control.^F-9

Tooling Design and Stamping Process Contributions to Springback

An American Iron and Steel Institute study defined several tool and process parameters that reduced angular change and side wall curl (Figures 23 and 24). As expected, angular change and curl increase with yield strength. Tighter clearances, smaller punch radii, and higher drawbead restraining forces reduced both types of springback.^S-47

Figure 23: The effect of tool parameters in angular change. The lower values are better.^S-47

Figure 24: The effect of tool parameters in sidewall curl. Higher values of radius of curl are better.^S-47

Figure 25 highlights the importance of keeping the die clearance as tight as allowed by formability and press capability. Unwanted bending and unbending work hardens the sheet metal and promotes increases in springback.

Figure 25: Reducing die clearance restricts additional bending and unbending as the sheet metal comes off the die radius, minimizing angular change.^Y-2

Figure 26 illustrates that angular change increases dramatically for higher strength steels as the bend radius increases. Minimizing angular change requires designing the punch radius as sharp as formability and product/style allows. However, with AHSS grades, sharp radii may promote the local formability failure mode of shear fracture. Inside product feature radii should be a minimum of 3T for any AHSS grade having a tensile strength at or above 590 MPa. Die radii at draw beads, punch openings, etc., where the material is pulled under tension over a radius should be at least 5T for any AHSS grade over 590 MPa. Minimum bend radii requirements may be even greater as strength levels continue to increase, roll forming excluded. To avoid problems due to specifying the wrong AHSS grade for the wrong application, bend testing and hole expansion testing should be used in conjunction with close communication with the steel supplier when selecting the proper die radius for the intended AHSS material. In addition, sharp radii contribute to excessive thinning at the tangent to the radius when global formability failures are of concern.

Figure 26: Angular change increases with yield strength and bend radius at a constant thickness.^S-2

Case Study in Springback Reduction Strategies

Automakers face conflicting constraints of lightweighting while improving safety performance. The B-Pillar Inner plays a significant role in meeting ever-increasing roof crush and side impact performance requirements. A study^M-17 published in 2007 showed the tooling and design changes made when transitioning from HSLA 340/440 to DP 550/980. These changes, shown in Figure 27, include adding sidewall beads to control springback, along with geometry to improve section stiffness.

Figure 27: Strategies to reduce springback in a DP 550/980 B-Pillar Inner.^M-17

Another approach is highlighted in a Webinar from 2020.^S-105  When forming hat-shaped sections, sidewall curl is minimized by using a cam to form the sidewall-flange area, followed by a more conventional sidewall stretch at the end (Figure 28).  The animation in Figure 29 shows the process.^S-6

Figure 28: Cam bending of sidewall-flange area minimizes springback.^S-105

Figure 29: Animation of hat-section forming process to minimize springback.^S-6

Compressive Stress Superposition for Springback Reduction

As explained above, springback and curl initiate when there are tensile stresses on one surface and compressive stresses on the other surface of the sheet. One of the keys to springback reduction is balancing these stresses through the sheet thickness.
A patented process known commercially as Smartform® relies on compressive stress superposition to achieve this stress balance. ^{B-76 , L-65, B-77,}, ^V-23

Achieving compressive stress superposition uses a two-step process where in the first preform step, the blank is formed into a “U” shape having a similar contour to the finished component, and then a sizing step to adjust the dimensional accuracy. This second step compresses the sheet metal during sizing rather than making it thinner from a drawing operation.
In the preforming stage (OP20), geometrical flexibility in the design of the tool surface exists, as the final component contour is not set until the sizing calibration stage (OP30). This allows for enlarged radii and wall angles to be used as countermeasures to prevent wrinkling and cracks.

Since the preform is not drawn, the starting blank can be cut to almost the same size as its final geometry before it is formed, reducing the number of trimming operations in the die process, as well as the amount of material used. Reportedly, an average of 15 percent materials savings occurs relative to conventional types of forming, with the actual savings being dependent on the size and complexity of the component.

Another benefit: resulting from the way the stress balance is achieved, this technology is relatively insensitive to variations in sheet metal properties, leading to a highly robust process.

Compressive stress superposition has been shown to work for steels having minimum specified tensile strength of 590 MPa through 1180 MPa.

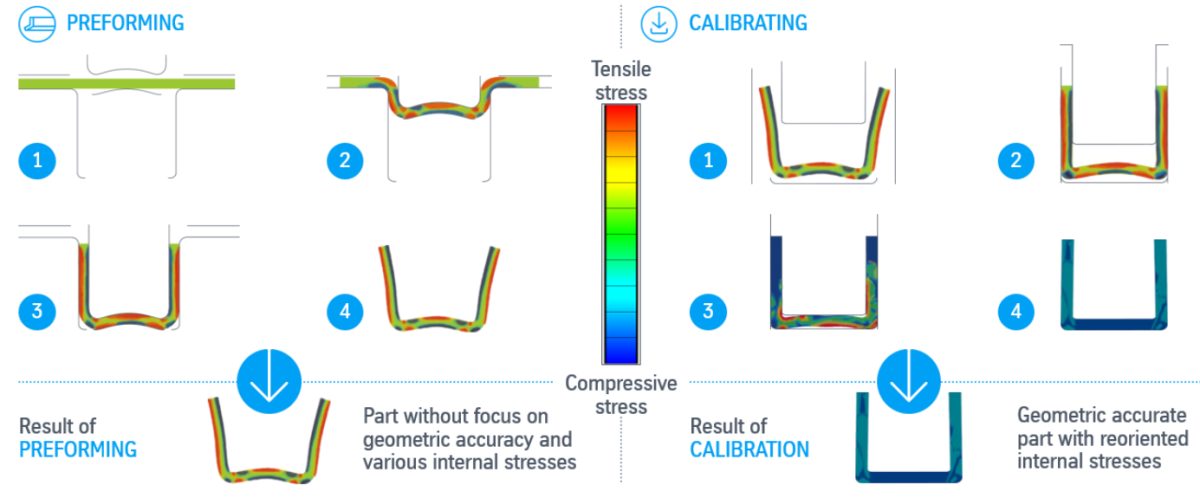
Figure 30: Compressive Stress Superposition Stress Conditions. Left: Preforming (OP20). Right: Sizing and Calibration (OP30). ^L-65

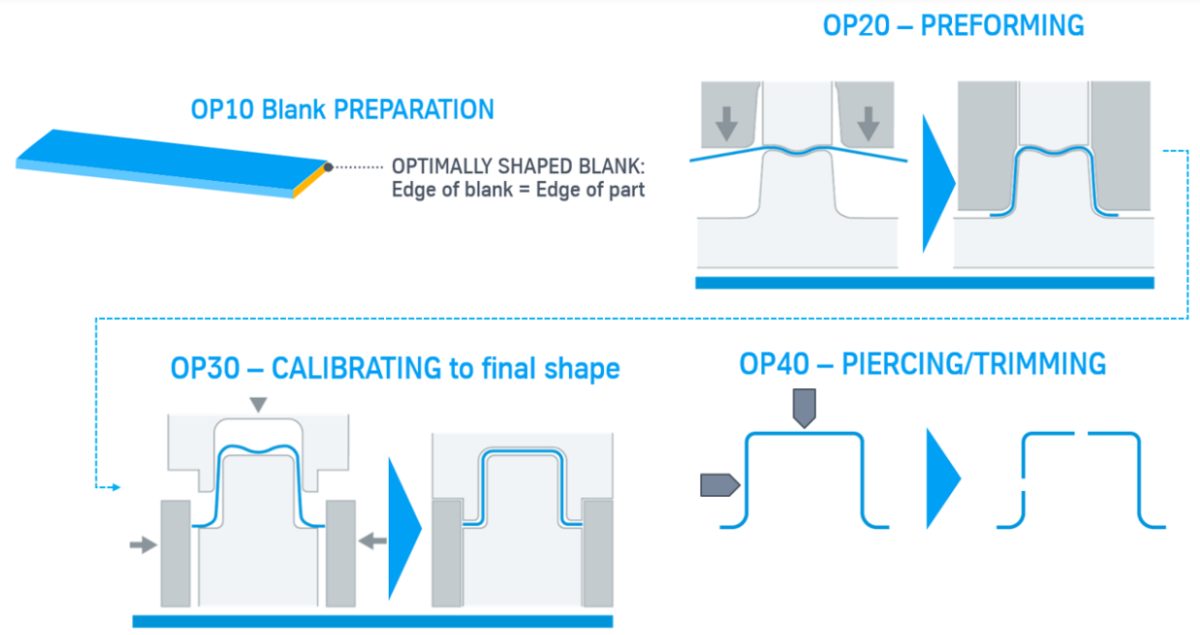
Figure 31: Compressive Stress Superposition Die Process.^L-65

Key Points

Several process and design modifications remove (or at least minimize and stabilize) the different modes of springback found in channels and similar configurations:

• Open wall angles achieved with minimized metal flow over die radii minimize angular change and sidewall curl.
• Overbending accounts for angular change, allowing the part to spring back to the targeted dimensions. Subjecting the bending radius to compressive stresses at the bottom of the press stroke plastically deforms the sheet metal, minimizing the elastic stresses associated with springback. Note that this approach is less successful in addressing sidewall curl.
• Applying in-plane tension to the side walls after forming reduces springback. Methods include using stake-beads, hybrid beads, or active binder force control. However, with higher strength steels, it may be difficult to achieve sufficient stretch to the sidewall by simply increasing the blank holding force. Preventing metal flow into the wall during post-stretching may require lock beads. Bead geometry affects blank size and press requirements.
• Geometric stiffeners like darts, beads, and flanges lock elastic stresses in place preventing springback from occurring. Subsequent forming or trimming operations may relieve these stresses, resulting in dimensional distortion. In addition, the selected press must have the load and energy requirements to form these features.

Design the part and tool in such a way that springback is desensitized to variations in material, gauge, tools and forming processes (a robust system and process) and that the effects of springback are minimized rather than attempt to compensate for it.

The accuracy of forming simulation programs to predict springback continues to improve, especially if it incorporates a complete material characterization and the chosen model is appropriate for the challenges of the specific part and forming method. Even without full accuracy, springback simulations can predict the trend and test the effectiveness of proposed countermeasures. In all cases, verify predictions against physical measurements.

Back To Top

• Correcting Springback: Overview
• Correcting Springback by Changing the Elastic Stress Distribution: Post Stretch (Stake Beads)
• Correcting Springback by Changing the Elastic Stress Distribution: Over-Forming
• Correcting Springback by Reducing or Minimizing the Elastic Stresses
• Correcting Springback by Locking in the Elastic Stresses
• Tooling Design and Stamping Process Contributions to Springback
• Case Study in Springback Reduction Strategies
• Key Points