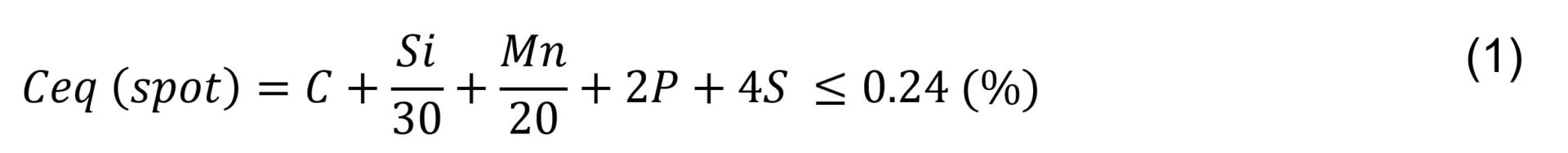Peel and chisel testing of resistance spot welds (RSW) in AHSS may produce fracture through the weld during destructive or teardown testing. This type of fracture becomes more common with increasing sheet thickness and BM strength. Weld metal fracture may accompany significant distortion of the metal immediately adjacent to the weld during testing. Such distortion is shown in Figures 1 and 2. Under these conditions weld metal fracture may not accurately predict serviceability of the joint. Weld performance of AHSS depends on microstructure, loading mode, loading rate, and degree of constraint on the weld.
Figure 1: Example of laboratory dynamic destructive chisel testing of DP 300/500 EG 0.65-mm samples.M-1
Figure 2: Example of laboratory dynamic destructive chisel testing of DP 350/600 GI 1.4-mm samples.M-1
Additionally, because of inherent stiffness of AHSS sheets, “nondestructive” chisel testing (Figure 3) on AHSS spot-welded panels will deform the panel permanently and may promote weld metal fracture. Therefore, this type of in-process weld check method is not recommended for AHSS with thicknesses greater than 1.0 mm. Alternative test methods should be explored for use in field-testing of spot welds in AHSS.
Figure 3: Semi-destructive chisel testing in 0.8-mm DP 300/500 EG.M-1
Ultrasonic nondestructive spot weld testing has gained acceptance with some manufacturers. It still needs further development before it can replace destructive weld testing completely. Some on-line real-time systems to monitor the resistance welding are currently available and are being used in some weld shops.
Weld-Shear Tension Strength
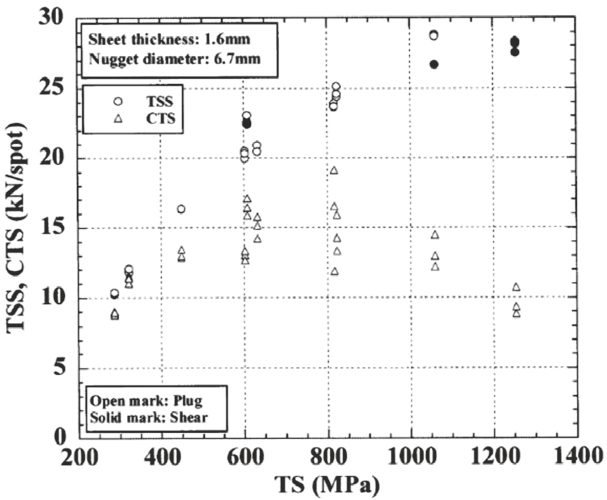
The Advanced High-Strength Steel (AHSS) weld tensile strength is proportional to material tensile properties and is higher than mild steel spot weld strength (Figure 4).
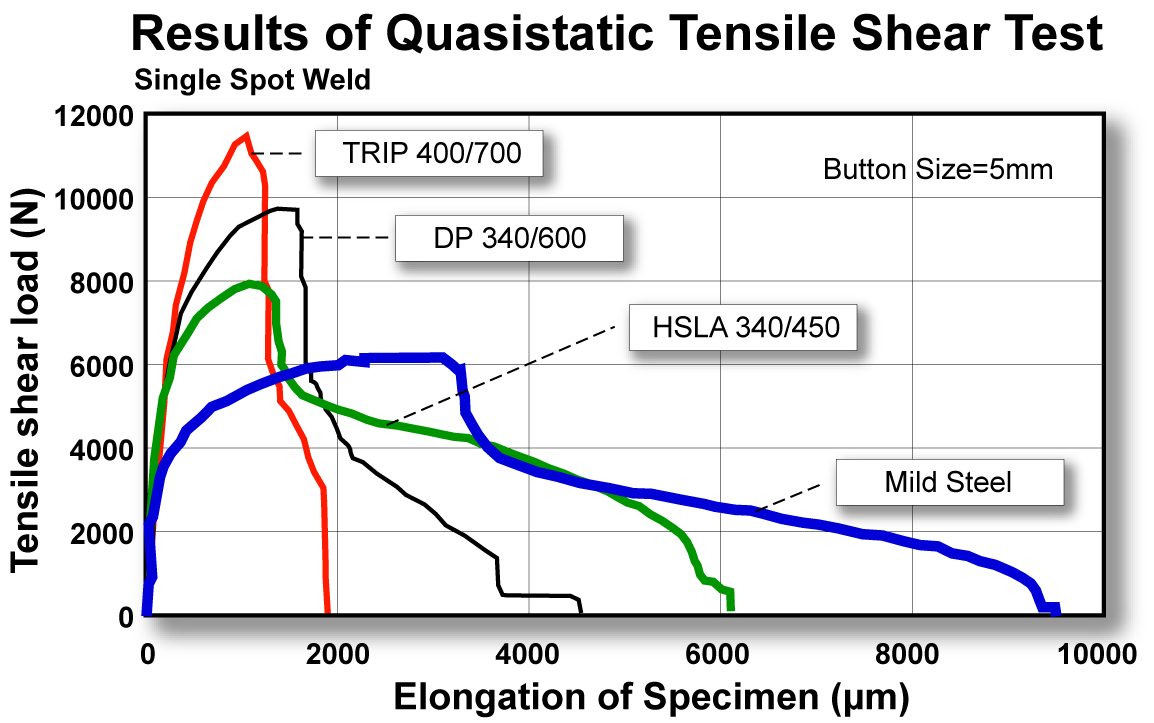
Figure 4: Tensile shear strength of single spot welds.L-4
While testing thick AHSS spot welds (from small button size to expulsion button) the fracture mode during shear-tension testing may change from interfacial to button pull out or plug. Despite interfacial fractures [Figure 5(a)], welds in AHSS may show high load-bearing capacity. In thin-gauge steels, the fracture is often in a button or plug (Figure 6).
Figure 5: Fracture modes in thick (1.87-mm) DP 700/980 CR during tension-shear testing.
Figure 6: Fracture modes in thin (0.65-mm) DP 300/500 EG during tension-shear testing.L-2
In a studyL-6, Finite-Element Modeling (FEM) and fracture mechanics calculations can be used to predict the RSW fracture mode and loads in shear-tension tests of AHSS. The results were compared to those obtained for an Interstitial Free (IF) steel. The results of the work confirmed the existence of a competition between two different types of fracture modes, namely Full Button Failure (FBF) pull-out and interfacial fracture. The force required to cause a complete weld button pull-out type fracture was found to be proportional to the tensile strength and to the thickness of the BM as well as the diameter of the weld. The force to cause an interfacial weld fracture was related to the fracture toughness of the weld, sheet thickness, and weld diameter. For High-Strength Steels (HSS), it was determined that there is a critical sheet thickness above which the expected fracture mode could transition from pull-out to interfacial fracture. In this analysis, it was shown that, as the strength of the steel increases, the fracture toughness of the weld required to avoid interfacial fracture must also increase. Therefore, despite higher load-carrying capacity due to their high hardness, the welds in HSS may be prone to interfacial fractures. Tensile testing showed that the load-carrying capacity of the samples that failed via interfacial fracture was found to be more than 90% of the load associated with a FBF pull-out. This indicates that the load-bearing capacity of the welds is not affected by the fracture mode. Therefore, the mode of fracture should not be the only criteria used to judge the quality of spot welds. The load-bearing capacity of the weld should be the primary focus in the evaluation of the shear-tension test results in AHSS.
Presently, some steel sheets have tensile strengths of 1,500 MPa or more. Such steels are subjected primarily to hot-press forming. The strengths of spot-welded joints are illustrated in Figure 7. The tensile shear strength of welded joints tends to increase with increasing steel sheet strength. Conversely, the Cross-Tension Strength (CTS) of welded joints tends to decline when the steel sheet strength is 780 MPa or more. This is thought to occur for the following reason. With increasing steel sheet strength, the stress concentration at the nugget edge increases, and nugget ductility and toughness decrease. When the amount of any added element [such as Carbon (C)] is increased in order to secure the desired steel sheet strength, the hardness of the weld metal (nugget) obtained increases; this, in turn, causes the nugget toughness to decrease. Nugget toughness also decreases when the contents of embrittling elements (P and S) are increased. The following equation of equivalent carbon content has been proposed to express the effects of these elements has been known.
Figure 7: Effect of tensile strength of steel sheet on TSS and CTS of spot-welded joints.
It is believed that C, Silicon (Si), and Manganese (Mn) contribute to the increase in nugget hardness and Phosphorus (P) and Sulfur (S) contribute to the increase in segregation, thereby causing a decline in nugget toughness. The threshold value on the right-hand side represents the strength of a welded joint and the soundness of the fracture mode in a cross-tension test. When the Ceq (spot) is within the range indicated by the above equation, fracture always occur outside the nugget (plug fracture) and CTS is high. However, attempts have been made to enhance CTS by controlling the composition of steel sheet appropriately. It was reported that even when the steel sheet strength is maintained constant, the strength of the weld increases as C content decreases and the Si content increases. This is thought to occur for the following reason. With the increase in C content, the hardness of the weld increases and the sensitivity of the fracture to the stress concentration at the nugget end increases, thereby causing CTS to decline. By contrast, as the content of Si – a hardenability element – is increased, the region that is quench-hardened by Si widens, that is, the change in hardness in the region from the nugget to the BM becomes milder, thereby improving CTS.
According to a well-known material mechanics model, it is expected that the CTS of the spot- welded joints will improve with the increase in steel sheet strength. However, this contradicts the observed phenomenon. Therefore, a cross-tension test was considered based on fracture mechanics and attempted to clarify the dominant factors of CTS.
Understanding the fracture of spot-welded joints in the cross-tension test as a problem of crack propagation from around the nugget, the problem was studied using an elastic-plastic fracture mechanics model in order to obtain a general understanding of fracture, from the ductile fracture to the brittle fracture. According to elastic-plastic fracture mechanics, it is assumed that the crack starts to propagate when the crack propagation driving force (J) around the nugget under a tensile load reaches the fracture toughness (Jc) of the nugget edge. Therefore, it was attempted to derive the value of J and measure the value of Jc of the edge during the cross- tension test.
Figure 8 shows the distribution of maximum principal stress at the nugget edge under a load of 4 kN. The broken line in the figure indicates the fusion line. It is clear that the virtual crack in the edge opened during the deformation. The decline in potential energy that was caused by the opening was divided by the crack area to obtain the value of J. Figure 9 shows the dependence of the J-value on nugget diameter under a load of 5 kN, obtained for each of the two types of cracks. It is clear that, in either cracking direction, the J-value under the same load decreases with the increase in nugget diameter. According to the analysis result obtained for a nugget diameter of 3 √t, the J-value when the crack was allowed to propagate in the interfacial direction was slightly larger than that when the crack was allowed to propagate in the sheet thickness direction. However, for larger nugget diameters (4 and 5 √t), the J-value when the crack was allowed to propagate in the sheet thickness direction became larger than that when the crack was allowed to propagate in the interfacial direction.
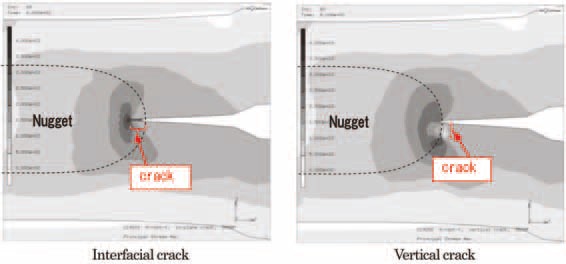
Figure 8: Deformed state and distribution of maximum principal stress at edge of nugget under the lead of 4 kN.N-5
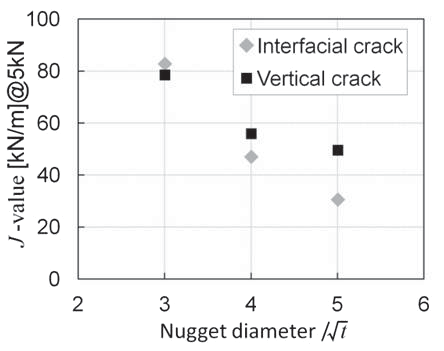
Figure 9: Dependence of J-value on nugget diameter under the load of 5 kN.N-5
In Figure 10, the fractured 0.30% C specimen revealed a grain boundary fracture at the edge and a cleavage fracture surface inside the nugget.
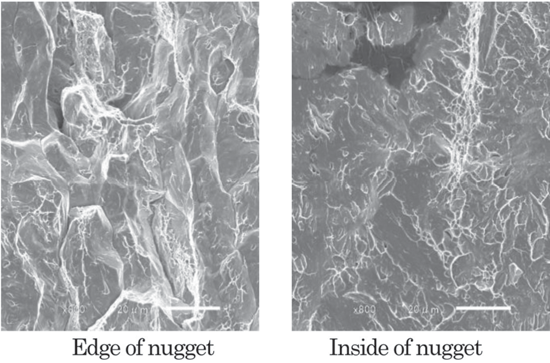
Figure 10: SEM images of fracture surface of miniature CT specimens after testing (0.30 mass % C).N-5
The CTS of welded joints was 2.4 kN for the 0.30% C steel sheet and 6.6 kN for the 0.13% C steel sheet, the ratio between them being 0.38. According to the fracture toughness test results, the fracture stress ratio [Jc (0.30% C)/Jc (0.13% C)]; the square root of J is proportional to stress) is 0.35. Thus, the above ratio was close to the test result. The 0.30% C joint subjected to the cross-tension test revealed a grain boundary fracture at the edge and a cleavage fracture surface inside the nugget.
Fracture Mode
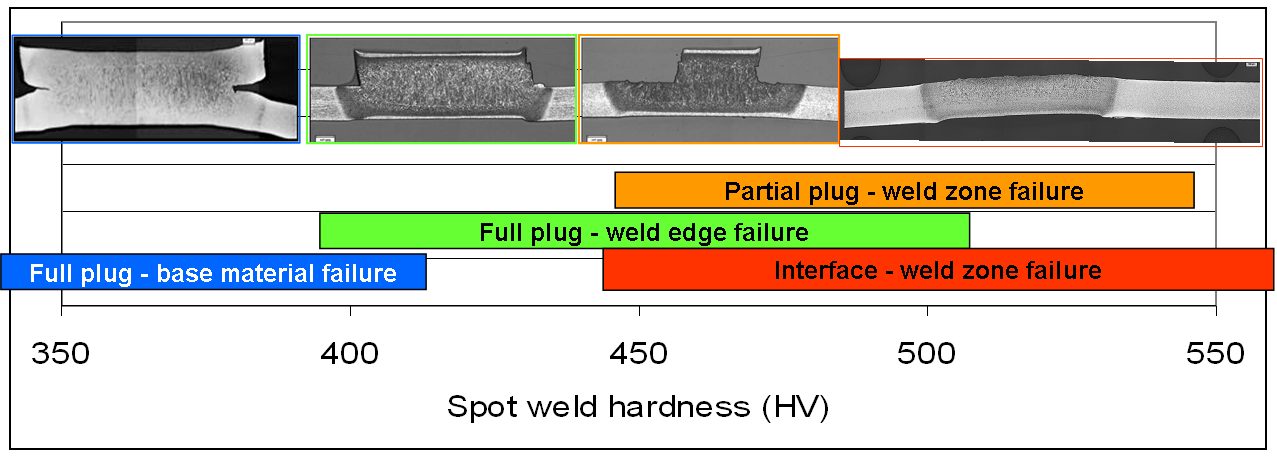
Several automotive and national specifications are using the criterion of fracture modes as an indication of weld quality in production when using AHSS. During peel and chisel testing, results vary from FBF appearance to a complete interface fracture. An example of the various fracture modes experience by the automotive industry is shown in Figure 11.
Figure 11: Peel and chisel test fracture modes in automotive industry.
There is an approximate relationship between hardness and fracture mode in resistance spot- welded joints. It is found that peel-type loading of resistance spot-welded joints (e.g., coach peel, cross-tension tensile, and chisel testing) begins to produce partial plug and interfacial fractures at hardness levels exceeding 450 Hardness Value (HV). The relationship between post-weld hardness and fracture mode in peel-type loading is illustrated in Figure 12. It can be seen that there are no set levels of hardness, where one type of fracture mode changes to another type of fracture mode. Instead, there is much overlap between the hardness levels, where specific fracture mode types occur. This indicates that post-weld hardness is not the only factor determining fracture mode.
Figure 12: Schematic relationship between RSW hardness and failure mode in peel-type loading.
There are various approaches to predict the fracture of spot welded joints by detailed numerical simulations. However, there are many issues such as the adequate recording of different fracture modes or a numerical methodology for dissimilar welds, which mostly appear in automotive structures. Therefore, a new simulation approach has been developed managing to close the existing gap. This method is based on different damage criteria for each spot weld zone (BM, HAZ, and weld) in order to capture all relevant fracture modes. The model parameters are identified via an inverse method on the basis of simple standardized test (tensile shear tests and peel test), which makes the application efficient. All relevant fracture modes (interfacial fracture and plug fracture) can be detected. A precise prediction of spot welds behavior for similar and dissimilar joints were demonstrated. The results show that the material parameters determined for one sheet thickness are transferable to investigations with differing sheet thicknesses. Consequently, the experimental effort to characterize substitute spot weld models for full car crash simulations can be reduced.
The determination of the specific model parameters for a similar weld combination of DP automotive application steel with a low yield stress and large ultimate strength was presented (thickness of 1.5 mm, ferrite matrix with areas of martensite). A characterization of the plastic flow behavior for each zone is required. For the BM a tensile test provides the flow curve in the region of uniform elongation. In order to capture the plastic flow behavior of the transformed zones in a physical manner, the BM curve is scaled by the averaged hardness change in the HAZ and the weld. To determine the Gurson model parameters for the HAZ, a static peel test is done. This loading results in a high stress concentration in the vicinity of the notch which leads to fracture initiation and evolution in the HAZ. The numerical damage parameters for the HAZ are fitted according to the experiment (Figure 13).
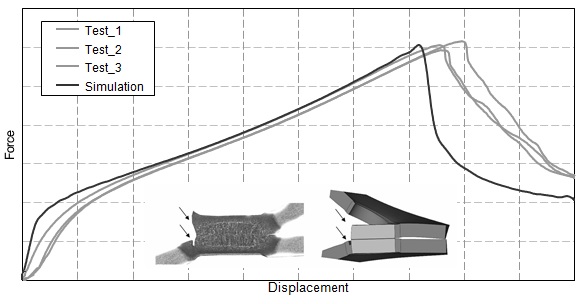
Figure 13: Parameter fitting for HAZ via peel test for DP steels.P-7