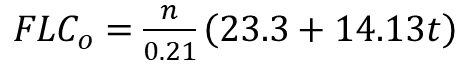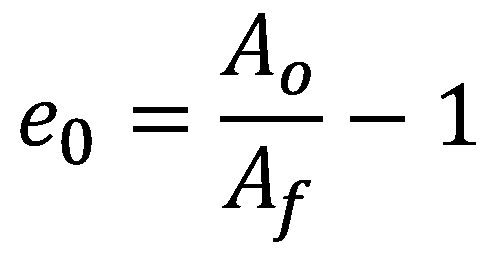
Formability, true fracture strain
topofpage
Fracture strain values derived from standard uniaxial tension tests can be used to evaluate automotive crashworthiness and forming behavior of aluminum alloys and Advanced High-Strength Steels (AHSS).Y-10, W-24, W-25, L-22, L-23, T-22, H-15, L-24 The true fracture strain (TFS) and similar concepts have emerged recently as intrinsic measures of local formability for AHSS. TFS is the true (logarithmic) strain associated with the “zero-gage-length” elongation at fracture (e0), where e0 is a conceptual engineering strain value based on an infinitesimal gage length in a tension test, where:
 Equation 1
Equation 1and Ao and Af are the cross-section area before testing and the fracture area after testing, respectively (constant volume assumed).D-13 It follows that TFS is defined as:
=ln \left( \frac{A_0}{A_f}\right)}) Equation 2
Equation 2
TFS is related to percent reduction of area at fracture (Z, %), where:
}) Equation 3
Equation 3
True Fracture Strain (TFS) Measurement Methods:
Fracture Area (Af)
Tensile test samples have a rectangular cross section before testing, indicated in the left image in Figure 1. The right image shows an idealized tension test specimen fracture surface, where five thickness measurement locations are indicated: two at the edges (ta, te); one at the center (tc), and two at the quarter-width positions (tb, td). Measured approximately at mid-thickness, wf is the fracture width. The dashed outline indicates the original specimen cross-section before testing (to·wo = Ao), and a 10-sided polygon (decagon) approximates the projected fracture area (Af), where the corners of the polygon correspond width-wise to the five thickness measurement locations.

Figure 1: Schematic representation of a tension test specimen before testing (left) and after fracture (right) viewed along the tensile axis.
From the dimensions portrayed in Figure 1, four possible methods to determine Af are indicated in Table 1—three lineal methods and one areal method.H-17 Method A uses a single thickness measurement at mid-width. Alternatively, for Method A the minimum thickness (tmin) may be used in cases where tc ≠ tmin. Method B uses a weighted three-thickness average A-24 —also known as the ASTM parabolic method.H-14, H-16 Method C uses a five-thickness average. For Method D, Af is the area of the polygon depicted in the left image of Figure 1.

Table 1. Fracture Area Measurement Methods.H-17
Dimensional measurements may be made quickly and conveniently with a calibrated digital microscope equipped with focal stacking capability and linked to image analysis software. Note that tf, wf and Af are respectively: the projected thickness, the projected width, and the projected area of the fracture surface. That is, to accommodate irregular and angled fracture surface features, measurements are made with respect to a virtual plane normal to the tensile axis. Alternatively, lineal measurements may be made with a conventional microscope equipped with a dial indicator or measuring stage. In this case, continual manual refocusing may be necessary to ensure true projected dimensional measurements.
Recently the effects of fracture area measurement method and tension test specimen type on fracture strain values were evaluated H-17. It was concluded that specimen type (i.e., width-to-thickness ratio) has a far greater impact on the consequent fracture strain value in contrast to that of measurement method. It was also advised that, when reporting fracture strain values derived from tension tests, the specimen type, the material thickness, and the fracture area measurement method be clearly indicated.
True Fracture Strain (TFS) Measurement Methods:
Fracture Types
Based solely on fracture appearance, various fracture types may be observed, with examples shown in Figure 2. H-17 The fracture type changes from Type 1 to Type 2 to Type 3 as the tension test specimen width-to-thickness ratio (wo/to) increases (left to right). Type 1 fracture is perpendicular to the tensile axis across the specimen width; Type 2 fracture is an irregular transition from Type 1 fracture to Type 3 fracture; and Type 3 fracture is aligned at an angle across the specimen width (~50-60° from the tensile axis).

Figure 2: Various fracture types observed in uniaxial tension testing, from left to right: Type 1 fracture (wo/to = 4.5—ASTM Standard Sub-size specimen); Type 2 fracture (wo/to = 12.8—ASTM Standard specimen); and Type 3 fracture (wo/to = 16.8—JIS No. 5 Standard specimen); The original width-to-thickness ratio (wo/to) is measured within the gage section of the test specimen.H-17
A similar fracture orientation dependence on specimen width was reported for Dual Phase (DP) steels more than thirty years ago by researchers at the Colorado School of Mines.S-49 A 2018 publication W-23 confirmed this behavior for other AHSS types, and illustrated that the transitional behavior—in terms of critical width-to-thickness ratio—is material dependent.
Figure 3 shows example Type 1 and Type 3 fractures in cross-section at the mid-width position (corresponding to position tc in Figure 1). Type 1 fractures typically run at an angle through thickness (~50-55° from the tensile axis). While most Type 1 fractures resemble that shown in Figure 2 (left) and that shown in Figure 3a, occasional through-thickness chevron profiles and “cup and cone” W-23 type fractures have been observed for Type 1 fractures. Nevertheless, Type 1 fractures are roughly symmetric about a plane normal to the sheet surface at the mid-width position.

Figure 3. Examples of (A) Type 1 fracture, and (B) Type 3 fracture; Polished through-thickness cross-sections at the mid-width position; Tensile axis is horizontal.
Type 3 fractures invariably show localized necking in through-thickness cross-section as in Figure 3b. Therefore, Type 3 fractures are roughly symmetric about a plane parallel to the sheet surface at the mid-thickness position. Type 2 fractures have both Type 1 and Type 3 characteristics at different positions across the width and thus have no overall plane of symmetry. Various degrees of damage (void formation) are observed in through-thickness cross-sections of fractured specimens— for example, Figure 3. Citation H-18 contains a detailed compendium with more information on this topic.
ElsewhereW-23, L-21 it was explained that the idealized fracture thickness profile—as depicted in the right image in Figure 1—is applicable only to smaller width-to-thickness ratios (thicker, hot-rolled materials or narrower gage sections). For thinner, cold-rolled materials, or for wider gage sections, there is often no clear fracture thickness minimum at the mid-width position. In fact, in some cases a fracture thickness maximum at mid-width has been observed. Furthermore, occasional mid-thickness delamination renders the volume-constancy assumption in question, with associated implications in Equation 1
Formability Classification and Rating System
In 2016 the foundation for a formability classification and rating system was introduced for AHSSH-14, where formability performance expectations are distinguished by the relationships between true fracture strain (TFS) and true uniform strain in a tension test. Such performance mapping concepts continue to be explored and modified by steelmakersH-16, W-23, L-21, D-12, W-22, V-5, R-6, S-48 by automakersH-18, H-19 and by international industry consortiums.G-20 Traditionally AHSS performance has been represented by the product of ultimate tensile strength and total elongation (UTS x TE) and relative position on the so-called “banana diagram” or Global Formability Diagram. While this conventional methodology discriminates behavioral extremes, much is lost regarding the nuances of local formability.
Intrinsic Formability Parameters
Widely considered an intrinsic measure of global formability, the true uniform strain (εu) is the logarithmic strain associated with uniform elongation (UE, %) in a uniaxial tension test, where:
}) Equation 4
Equation 4Example TFS and εu values are shown for a series of 980-class AHSS (980 MPa minimum tensile strength) in Figure 4H-14. In this analysis, TFS values ranged from less than 0.5 [DP 980 (LSi)] to more than 1.0 (CP 980), and εu values ranged from 0.05 (CP 980) to 0.15 (GEN3 980). The Third Generation AHSS materials (GEN3-type) have the largest εu values, and the Multi-Phase/Complex-Phase steels (MP/CP-type) have the largest TFS values. As a group the Dual Phase steels (DP-type) have intermediate εu values and a wide range of TFS values. As illustrated in Figure 4, TFS is far greater than εu. A similar disparity between fracture strain and uniform strain was shown in Citation D-14, and no consistent relationship between the two parameters was determined.

Figure 4: True uniform strain (εu) and true fracture strain (TFS) values for a series of 980-class AHSS; Error bars show the range among three test specimens for each material.H-14
The local/global strain ratio (L/GSR) and the formability index are key parameters to guide application-specific material selection and to help set targets for future AHSS grade developments.H-14, H-16 The L/GSR reflects the relative preponderance of local formability to global formability and is defined as:
 Equation 5
Equation 5
The L/GSR is useful in understanding relative intrinsic formability “character”. Materials with higher relative TFS values are naturally expected to perform better under flanging, edge stretching and tight-radius bending conditions [e.g., MP 980 (LCE) and CP 980 in Figure 4], while materials with higher relative uniform strain values (i.e., higher terminal n values) are better suited for stretch forming and are able to distribute strain more uniformly (e.g., GEN3 980 and GEN3 980-HY in Figure 4).
Furthermore, the formability index (F.I. in the formula) is defined as:
 Equation 6
Equation 6This index represents an intermediate strain value between εu and TFS and provides a convenient measure of the overall formability expectation, where both local formability and global formability are considered. As an example, Figure 5 shows an exponential relationship between F.I., and the limiting bend ratio (r/t) determined from 90° V-bend testing for the same series of 980-class AHSS represented in Figure 4.H-14 It was reasoned that in the early stages of deformation, global formability (εu) dictates the strain distribution around the punch nose, while fracture resistance is governed by local formability (TFS) in the latter stages of deformation.

Figure 5. Correlation between the limiting bend ratio (f) and the formability index (F.I.) for a series of 980-class AHSS. A higher formability index corresponds to a lower (better) limiting bend ratio in 90° V-bend testing.H-14
Local/Global Formability Map
Figure 6 illustrates the essential framework of the local/global formability map—known eponymously as the Hance diagram.H-14, D-12, G-20 Here, the dashed lines represent the boundaries between global character (L/GSR < 5), balanced character (5 < L/GSR < 10), and local character (L/GSR > 10). The continuous curves represent arbitrary iso-F.I. contours corresponding to the values indicated (in parentheses). The qualitative assessments (Poor through Excellent) indicated for each formability level are also arbitrary; however, these performance level monikers were chosen to reflect real-world experience. Portrayed in this way (in contrast to Figure 4, for example), the relationships between true fracture strain and true uniform strain are more discernable, and both the formability character and the formability level become apparent.

Figure 6: Essential framework of the local/global formability map concept.H-16
Case Study Using the Local/Global Formability MapH-15
The basic utility of the local/global formability map concept was demonstrated for an automotive seating system development program.H-15 In this case study, stamping trials were conducted with two 980-class AHSS (980 MPa minimum UTS designation):
- 1.6mm 980DP(LSi): A classic Dual Phase (DP) ferrite/martensite steel with low silicon content (LSi), and
- 1.6mm 980MP(LCE)—a Multi-Phase (MP) steel with high yield strength and low carbon equivalent (LCE).
Basic formability parameters are summarized in Table 2 for the trial materials. Based solely on elongation values (UE, TE), one might have concluded that the formability of 980DP(LSi) would exceed that of 980MP(LCE).

Table 2. Formability Parameters for Two 980-Class AHSS.
However, the stamping trial results were counterintuitive and drastically different among the two trial materials. The 980DP(LSi) material exhibited severe edge-cracking in multiple locations, while the 980MP(LCE) material ran without issue. Both materials were free of necking-type failures as predicted by computer simulations (sufficient global formability). An example part overview is shown in Figure 7. Typical 980DP(LSi) edge cracks are shown in Figure 8 for a pierced/extruded hole (Location 1) and for a blanked/stretched perimetric edge (Location 2). Clearly, relative sheared-edge ductility may not simply be deduced from conventional tensile elongation values.
![Figure 7: Overview of a stamped automotive seating component [length ~ 480 mm (19 in.)]. H-15](https://ahssinsights.org/wp-content/uploads/2020/10/2.3.5a-Figure7.svg)
Figure 7: Overview of a stamped automotive seating component [length ~ 480 mm (19 in.)].H-15
![Figure 8: Close-up views of Location 1 (left) and Location 2 (right) identified in Figure 7 [material: 980DP(LSi)]; Location 1 is a pierced hole that was extruded during forming, and Location 2 is a blanked perimetric edge that was stretched during forming (underside with respect to Figure 7). H-15](https://ahssinsights.org/wp-content/uploads/2020/10/2.3.5-Fig8.jpg)
Figure 8: Close-up views of Location 1 (left) and Location 2 (right) identified in Figure 7 [material: 980DP(LSi)]; Location 1 is a pierced hole that was extruded during forming, and Location 2 is a blanked perimetric edge that was stretched during forming (underside with respect to Figure 7).H-15
The local/global formability map coordinates of the 980DP(LSi) and 980MP(LCE) trial materials are shown in Figure 9. With reference to the framework described in Figure 6, 980DP(LSi) exhibits global/balanced character with an overall borderline rating of Fair/Good (F.I. = 0.20); while 980MP(LCE) has decidedly local character with an overall rating of Good (F.I. = 0.26). Furthermore, the TFS value of 980MP(LCE) is more than twice that of 980DP(LSi).

Figure 9: Local/global formability map featuring three 980-class AHSS—980DP(LSi), a classic DP ferrite/martensite steel with low silicon content (LSi); 980MP(LCE), an MP steel with high yield strength and low carbon equivalent (LCE); and 980GEN3, a third generation AHSS. Image based on Citations H-15 and H-17.
As an independent confirmation of the local formability advantage of 980MP(LCE), the hole expansion ratio (HER, λ) is more than four times that of 980DP(LSi) (Table 2). A strong correlation between TFS and λ has been confirmed by several authors L-22 L-23 T-22 H-15 As the component featured in this case study is dominated by extremely challenging edge-stretching conditions, 980MP(LCE) is the clear wiser material selection. However, in applications with more demanding global formability requirements, other issues such as intolerable strain localization could arise, and a third generation AHSS might be the best choice. As an example, when contrasting 980GEN3 AHSS (third generation AHSS) to 980DP(LSi) in Figure 9, the intrinsic global and local formability parameters (εu and TFS), as well as the F.I, are approximately 50% greater.
True Fracture Strain (TFS): Alternatives to TFS
While the local/global formability map methodology was developed in the context of true fracture strain (TFS), there are other ways to represent intrinsic local formability (fracture resistance) with data derived from standard uniaxial tension tests. In the original conception (Hance diagram), true uniform strain (εu) and TFS are two points along a logarithmic strain continuum from zero to fracture, and the relationships between these values elegantly describe the formability character (local/global strain ratio) and the overall formability level (formability index). The “best” local formability parameter may be a matter of practicality or applicability, or simply a matter of preference. Each method has its strengths and weaknesses, and such fracture strain concepts continue to evolve.
True Thinning Strain at Fracture
The true fracture strain (TFS) value is an area-based measurement of fracture strain and thus reflects the tension test specimen width change as well as the thickness change, for better or for worse. Citation H-18 suggests that the true thinning strain at fracture (ε3f) is a more appropriate measure of local formability, where:
\right| = ln \left(\frac{t_0}{t_f}\right)}) Equation 7
Equation 7
and to and tf are the original thickness (before testing) and final thickness (after fracture). By convention ε3f is a positive value and represents the absolute value of the true thickness strain at fracture (a negative value). Furthermore, the post-uniform portion of the fracture strain may be isolated by subtracting the uniform component of thinning strain, where:
}) Equation 8
Equation 8and εu and r are the true axial uniform strain and the plastic strain ratio (normal anisotropy) measured during the tension test, respectively. Post-uniform fracture strain components might be more relevant to materials with high uniform elongation values such as TWIP steels H-18. In a similar way, the post-uniform portion of the area-based TFS value may be expressed as:
 Equation 9
Equation 9
Another study W-23 concluded that: (1) area-based fracture strain measurements such as TFS result in less experimental scatter when compared to thickness-based fracture strain measurements such as ε3f, and (2) area-based measurements show less dependence upon the method by which fracture strains are determined. It appears that a single thickness measurement may misrepresent the fracture strain and that a multiple-thickness (average thickness) or area measurement approach may be more stable.
Critical Fracture Strain
Perhaps a lesser-known and under-exploited representation of fracture strain is the so-called critical fracture strain value (CFS)—introduced in 1999 for aluminum alloys in Citation Y-10 and re-visited in 2007 in the context of High-Strength Steel in Citation W-24. In concept CFS is the estimated true thinning strain at fracture, where:
*\frac{s_f}{s_u}\right] \approx \varepsilon_3_f}) Equation 10
Equation 10
In determining CFS, only the engineering stress-strain data from a uniaxial tension test are needed—that is, no post-fracture area or thickness measurements are required: eu is the engineering uniform strain value (% uniform elongation/100); sf is the engineering fracture stress; and su is the ultimate tensile strength or UTS. Figure 10 shows an example engineering stress-strain curve for a 980-class AHSS, where the parameters relevant to CFS are marked. In this example, CFS = -ln[(1-0.07/2)·(787/1015)] = 0.29.

Figure 10: Example engineering stress-strain curve for a 980-class AHSS. Here, eu is the engineering uniform strain, su is the ultimate tensile strength (UTS), sf is the engineering fracture stress, CFS is the critical fracture strain, and ε3f is the true thinning strain at fracture.
True Fracture Strain (TFS):
Correlation to Hole Expansion Ratio
In a recent studyL-5, tensile properties (80 mm gage length) and hole expansion ratio were measure for AHSS with minimum tensile strength designations ranging from 600 to 1200 MPa, and thickness between 1 and 2 mm. No particular correlation was found between the hole expansion ratio and conventional tensile properties such as uniform elongation, total elongation, n-value, and so on.
The most promising relationship was found between the hole expansion ratio (converted to logarithmic strain) and the true thinning strain at fracture in tension. This relationship is illustrated in Figure 11 for total thinning strain (ε3f, Equation 7) on the left, and for post-uniform thinning strain (ε*3f, Equation 8) on the right. In both cases, better correlation is shown for transverse tension tests rather than for longitudinal tension tests (linear fit through the origin).

Figure 11: Hole expansion ratio (logarithmic strain) as a function of true thinning strain at fracture. Left graph: total thinning strain (ε3f); Right graph: post-uniform thinning strain (ε*3f).L-5
While the above correlations are good, the inherent scatter associated with the hole expansion test, fracture strain measurements, and other local formability parameters may limit applicability in a production environment. Furthermore, various factors affect hole expansion in production environments, including hole preparation technique, edge condition, and cutting clearance.
Standardization: VDA 238-110 for industrial applications of TTS (True Thickness Strain) and TFS (True Fracture Strain)
2023 saw the release of the first Industry standard method of using fracture surfaces from tested tensile bars to characterize local ductility. VDA 238-110V-25 covers industrial application of TTS (True Thickness Strain at fracture at minimum thickness) and TFS (True Fracture Strain from area reduction) to quantify local ductility based on the postmortem microscope analysis of the fracture surface of tensile test samples.
Shortly thereafter was the publicationL-72 of a detailed study evaluating the gauge repeatability and reproducibility (GRR) based on round-robin test results from 18 labs, spanning close to1500 tests of three AHSS grades: CR440Y780T-DH, CR780T980T-CP, and HR660Y760T-CP. Conclusions from this study include:
- For the three grades evaluated, the greatest total variance of hole expansion results associated with punched holes
- Measurement variance of TTS testing is comparable to that of elongation at breakage measurements, and substantially lower than seen in hole expansion testing.
- For the two complex phase steels, TTS and TFS results are very similar, whereas in the high ductility dual phase (DH) grade, the TFS value is slightly higher than TTS. The larger TFS value may be related to the higher global ductility of the DH grade compared to the CP steels. TFS includes a contribution of both thickness and width reduction, leading to a comparatively high value, while TTS represents the thickness reduction. As such, TTS may be a more conservative, but more representative value of local formability material capability.H-18 In addition, characterizing TTS may be experimentally simpler than TFS.
The VDA 238-110 testV-25 is relatively recent, and is not as mature as tensile testing which has had a continually revised standard procedure for over 100 years [ASTM E8 was first issued in 1924]. Aspects of VDA 238-110 that may need to be addressed in future revisions include these observations from Citation L-75:
- Tensile sample failure location – the minimum thickness at fracture may not be located at the sample center.
- Cracks may form at the sample shoulders leading to premature failure – the validity of these results should be questioned.
- Edge cracks starting normal to the tensile direction, typically without significant necking and an asymmetric fracture shape pattern, may not be a good measure of bulk local ductility.
- The real fracture shape border may be best seen in three-dimensions rather than a 2-D representation. Otherwise, it is possible to produce false values for reduction of area and/or minimum thickness values.
- There is ambiguity in the definition of thickness close to sample edges. Thickness is defined as the cross section of a vertical line with the sample fracture contourplot. If this line crosses “empty air” at the left/right outer edges of the broken tensile sample, then invalid readings may occur due to the definition.
- When measuring broken surfaces, there is still some subjectivity in the measurement, especially on surfaces with high fracture angle.
 |
Thanks are given to Brandon Hance, Ph.D., who contributed the majority of this article. |

Mechanical Properties
M-Value, Strain Rate Sensitivity
All metals strengthen as they are deformed through a process called work hardening. However, the degree of strengthening may change as a function of the speed at which they are tested. In these cases, when local necking starts, the strain rate in the necked area is different in the surrounding non-necking region.
With negative strain-rate sensitivity, as is the case with many aluminium alloys, the necked region is weaker than the surrounding area. Fracture occurs with very little additional strain after necking initiation.
With positive strain-rate sensitivity, the necked region is stronger than the surrounding area. This is the basis for many steel alloys having a total elongation to fracture that is nearly double that of uniform elongation.
This strain-rate sensitivity is described by the exponent, m, in the modified power law equation:
 Equation 1
Equation 1
where έ is the strain rate and m is the strain rate sensitivity.
To characterize the strain rate sensitivity, medium strain rate tests were conducted at strain rates ranging from 10-3/sec (commonly found in tensile tests) to 103/sec. For reference, 101/sec approximates the strain rate observed in a typical stamping. Both yield strength and tensile strength increase with increasing strain rate, as indicated Figures 1 and 2.

Figure 1: Influence of Strain Rate on Yield Strength.Y-1

Figure 2: Influence of Strain Rate on Tensile Strength.Y-1
Up to a strain rate of 101/sec, both the YS and UTS only increased about 16-20 MPa per order of magnitude increase in strain rate. These increases are less than those measured for low strength steels. This means the YS and UTS values active in the sheet metal are somewhat greater than the reported quasi-static values traditionally reported. However, the change in YS and UTS from small changes in press strokes per minute are very small and are less than the changes experienced from one coil to another.
The change in n-value with increase in strain rate is shown in Figure 3. Steels with YS greater than 300 MPa have an almost constant n-value over the full strain rate range, although some variation from one strain rate to another is possible.

Figure 3: Influence of Strain Rate on n-value.Y-1
Similar behavior was noted in another studyB-22 that included one TRIP steel and three DP steels. Here, DP1000 showed a 50% increase in yield strength when tested at 200/sec compared with conventional tensile test speeds. Strain rate has little influence on the elongation of AHSS at strain rates under 100/sec.
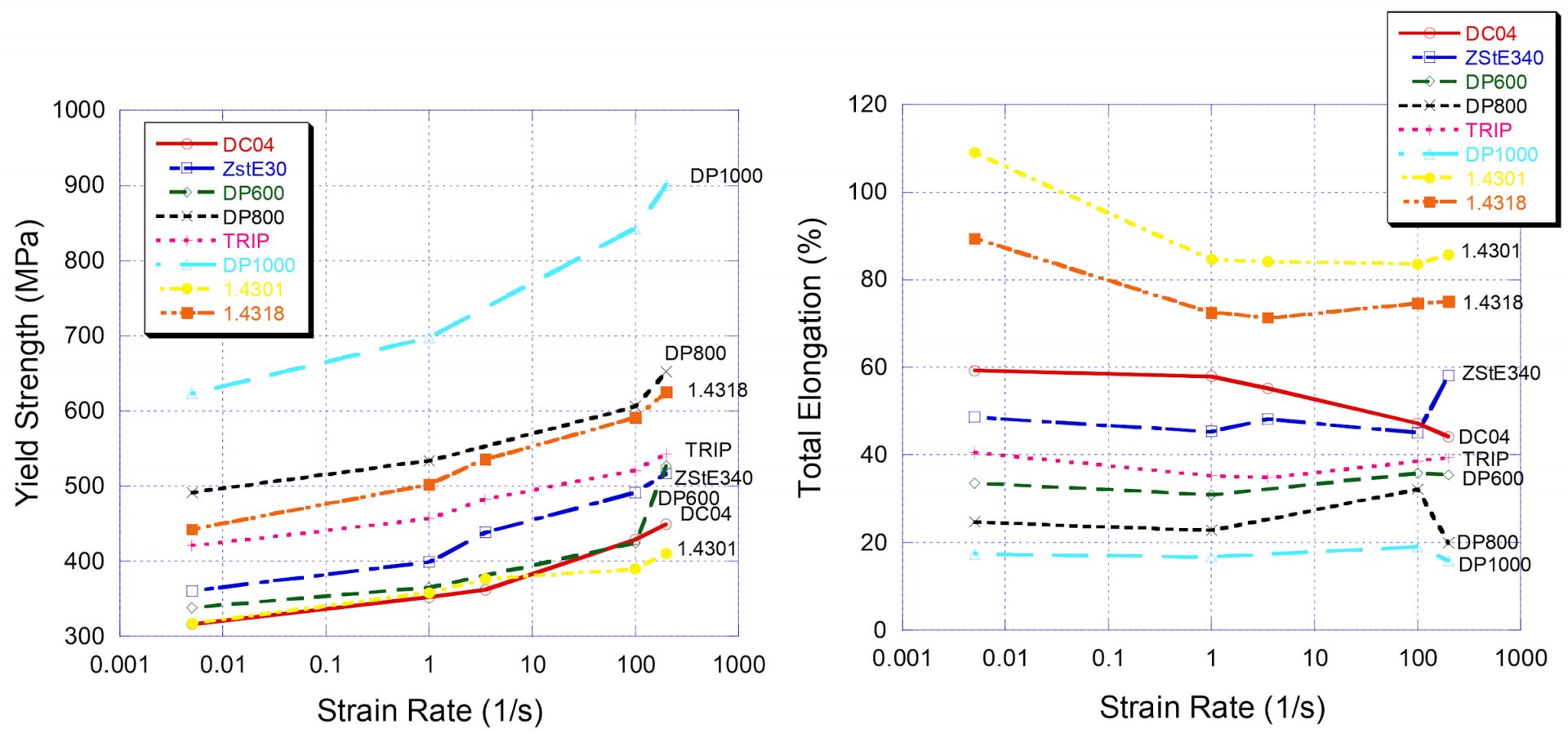
Figure 4: Relationship between strain rate and yield strength (left) and elongation (right). Citation B-22, as reproduced in Citation D-44
Figure 5 shows the true stress-true strain curves for a processed Press Hardened Steel tested at different strain rates. The yield stress increases approximately five MPa for one order of magnitude increase in strain rate.

Figure 5: True stress-strain curves at different strain rates for 1mm thick Press Hardening Steel (PHS) after heat treatment and quenching.V-1
The tensile and fracture response of different grades is a function of the strain rate and cannot be generalized from conventional tensile tests. This has significant implications when it comes to predicting deformation behavior during the high speeds seen in automotive crash events. See our page on high speed testing for more details.
![Crash Management]()
Crash Management, structural performance
In addition to enhanced formability, Advanced High-Strength Steels (AHSS) provide crash energy management benefits over their conventional High-Strength Steel (HSS) counterparts at similar strength levels. Higher levels of work hardening and bake hardening at a given strength level contribute to this improvement in crash performance.
The energy required for plastically deforming a material (force times distance) has the same units as the area under the true stress-true strain curve. This applies to all types of plastic deformation – from that which occurs during tensile testing, stamping, and crash. The major difference between these is the speed at which the deformation takes place.
As an example, consider the press energy requirements of two grades by comparing the respective areas under their true stress – true strain curves. The shape and magnitude of these curves are a function of the yield strength and work hardening behavior as characterized by the n-value when tested at conventional tensile testing speeds. At the same yield strength, a grade with higher n-value will require greater press energy capability, as highlighted in Figure 1 which compares HSLA 350/450 and DP 350/600. For these specific tensile test results, there is approximately 30% greater area under the DP curve compared with the HSLA curve, suggesting that forming the DP grade requires 30% more energy than required to form a part using the HSLA grade.

Figure 1: True stress-strain curves for two materials with equal yield strength.T-3
The high degree of work hardening exhibited by DP and TRIP steels results in higher ultimate tensile strength than that exhibited by conventional HSS of similar yield strength. This provides for a larger area under the true stress-strain curve. Similarly, when panels are formed from these grades, the work hardening during forming leads to higher in-panel strength than panels from HSS of comparable yield strength, further increasing the area under the stress-strain curve, ultimately resulting in greater absorption of crash energy.
Finally, the high work-hardening rate better distributes strain during crash deformation, providing for more stable, predictable axial crush that is crucial for maximizing energy absorption during a front or rear crash event.
Many AHSS are bake hardenable. The relatively large BH effect also increases the energy absorption capacity of these grades by further increasing the area under the stress-strain curve. The BH effect adds to the work hardening imparted by the forming operation. Conventional HSS do not exhibit a strong BH effect and therefore do not benefit from this strengthening mechanism.
Figure 2 illustrates the difference in energy absorption between DP and TRIP steels as a function of their yield strength determined at quasi-static tensile testing speeds.

Figure 2: Absorbed energy for square tube as function of quasi-static yield strength.T-2
Figure 3 shows calculated absorbed energy plotted against total elongation for a square tube component. The absorbed energy remains constant for the DP and TRIP steels but the increase in total elongation allows for formation into complex shapes.

Figure 3: Calculated absorbed energy for a square tube as a function of total elongation.T-2
For certain parts, conventional steels may have sufficient formability for stamping, yet lack the required ductility for the desired crash failure mode and will split prematurely rather than collapsing in a controlled manner. AHSS grades improve energy absorption by restoring a stable crush mode, permitting more material to absorb the crash energy. The increased ductility of AHSS grades permit the use of higher strength steels with greater energy absorbing capacity in complex geometries that could not otherwise be formed from conventional HSS alloys.
Stable and predictable deformation during a crash event is key to optimizing the steel alloy selection. The ideal profile is a uniform folding pattern showing progressive buckling with no cracks (Figure 4).

Figure 4: Deformation after axial crushing.A-49
Achieving crack-free folds is related to the local formability of the chosen alloy. Insufficient bendability can lead to early failure (Figure 5). Research to determine proper simulation inputs with physical testing for verification.

Figure 5: Three-point bend testing of two DP980 products having different folding and cracking behavior resulting from different microstructures and alloying approaches.B-12
High Strain Rate Property Test Methods
for Steel and Competing Materials
Tensile testing occurs at speeds that are 1000x slower than typical automotive stamping rates. Furthermore, automotive stamping is done at speeds that are 100x to 1000x slower than crash events. Stress-strain responses change with test speed – sometimes quite dramatically.
The m-value is one parameter to characterize this effect, since it is a measure of strain rate sensitivity. Generally, steel has more favorable strain rate effect properties compared with aluminum, but this is also a function of alloy, test temperature, selected strain range, and test speed. L-20
These reasons form the background for the need to characterize the intermediate and high strain rate behavior of AHSS.
![Crash Management]()
Formability
topofpage
If all stampings looked like a tensile dogbone and all deformation was in uniaxial tension, then a tensile test would be sufficient to characterize the formability of that metal. Obviously, engineered stampings are much more complex. Although a tensile test characterizes one specific strain path, a Forming Limit Curve (FLC) is necessary to have a map of strains indicating the onset of critical through-thickness necking for different linear strain paths. The strains which make up the FLC represent the limit of useful deformation. Calculations of safety margins are based on the FLC (Figure 1).

Figure 1: General graphical form of the Forming Limit Curve.E-2
Picturing a blank covered with circles helps visualize strain paths. After forming, the circles turn into ellipses, with the dimensions related to the major and minor strains. This forms the basis for Circle Grid Strain Analysis.
Generating Forming Limit Curves from Equations
Pioneering work by Keeler, Brazier, Goodwin and others contributed to the initial understanding of the shape of the Forming Limit Curve, with the classic equation for the lowest point on the FLC (termed FLC0) based on sheet thickness and n-value. Dr. Stuart Keeler was the Technical Editor of these AHSS Guidelines through Version 6.0, released in 2017.
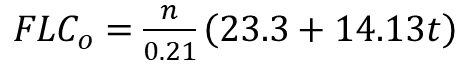 |
Equation 1 |
These studies generated the left hand side of the FLC as a line of constant thinning in true strain space, while the right hand side has a slope of +0.6, at least through minor (engineering) strains of 20%.
Evidence accumulated over many decades show that this approach to defining the Forming Limit Curve is sufficient for many applications of mild steels, conventional high strength steels, and some lower strength AHSS grades like CR340Y/590T-DP. However, this basic method is insufficient when it comes to creating the Forming Limit Curves for most AHSS grades and every other sheet metal alloy. Grades with significant amounts of retained austenite experience significant deviations from these simple estimates.H-23, S-61 In these cases, the FLC must be experimentally determined.
Additional studies found correlation with other properties including total elongation, tensile strength, and r-valueR-8, P-19, G-23, A-45, A-46, H-23 with some of these attempting to define the FLC by equations.
Experimental Determination of Forming Limit Curves
ASTM A-47 and ISO I-16 have published standards covering the creation of FLCs. Even within these standards, there are many nuances left for interpretation, primarily related to the precise definition of when a neck occurs and the associated limiting strains.
There are two steps in creating FLCs: Forming the samples and measuring the strains.
Forming sheet specimens of different widths uses either a hemispherical dome (Nakajima or Nakazima method N-14) or a flat-bottom punch (Marciniak method M-22) to generate different strain paths from which critical strains are determined. The two methods are not identical due to the different strain paths generated from the punch shape. These differences may not be significant for many lower strength and conventional High-Strength Steels, but may deviate from each other at higher strengths or with advanced microstructures. Figure 2 highlights samples formed with the Nakajima method.
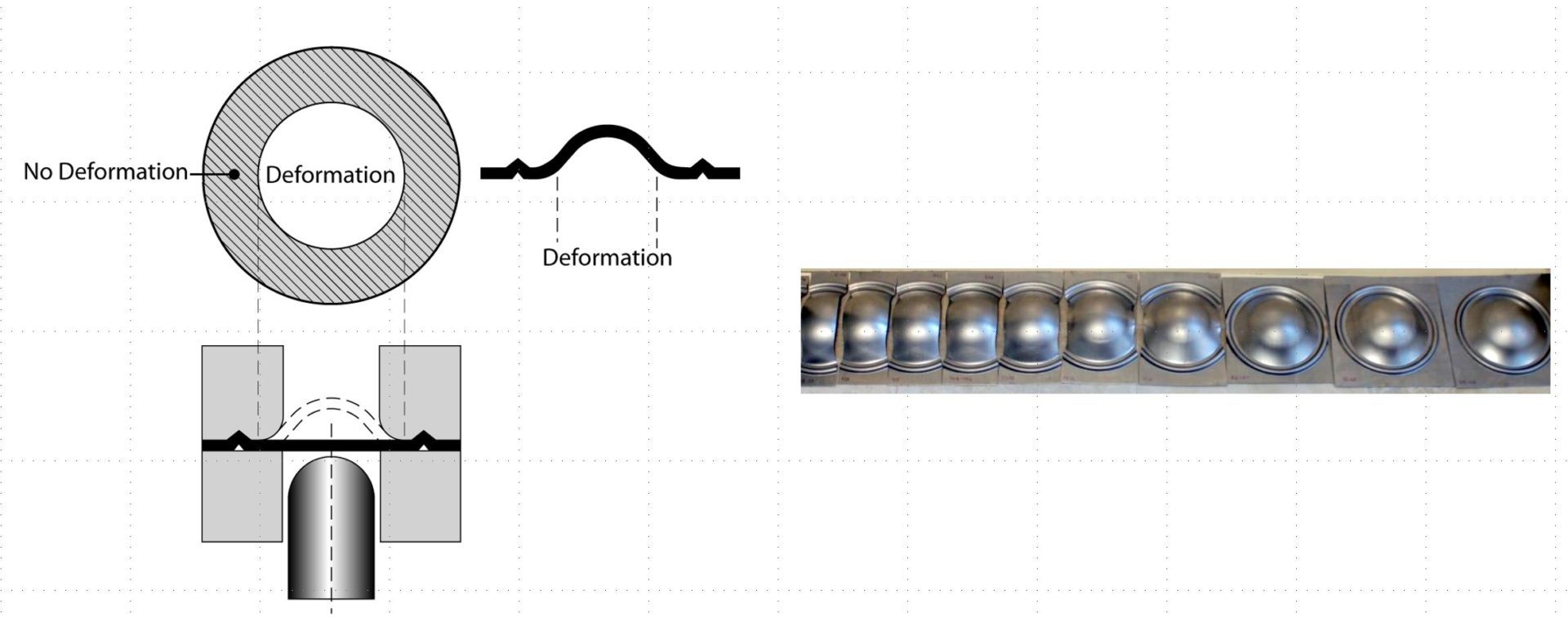
Figure 2: Forming limit curves can be created by deforming multiple samples of different widths. Narrow strips on the left allow metal to flow in from the unconstrained edges, creating a draw deformation mode leading to strains that plot on the left side of the FLC. Fully constrained samples, shown on the rightE-2, create a stretch deformation mode leading to strains that plot on the right side of the FLC.
Generally, strains are measured using one of two methods. The first approach involves covering the initially flat test samples with a grid pattern of circles, squares, or dots of known diameter and spacing to measure the strains associated with deformation. An alternate approach is based on Digital Image Correlation (DIC), where a camera tracks the movement of a random speckle pattern applied prior to forming.W-26, H-22, M-21 DIC methods are directly suited for use with stress-based FLCs.
Differences between Forming Limit Curves
and Forming Limit Diagrams
Often, the terms Forming Limit Curve (FLC) and Forming Limit Diagram (FLD) are used interchangeably. Perhaps a better way of categorizing is to define the components and what they encompass. This is somewhat of a simplification, since detailed interactions are known to occur.
- The Forming Limit Curve is a material parameter reflecting of the limiting strains resulting in necking failure as a function of strain path. It is a function of the metal grade, thickness, and sheet surface conditions, as well as the methods used during its creation (hemispherical/flat punch, test speed, temperature). It is applicable to any part shape.
- Deforming a flat sheet into an engineered stamping results in a formed surface with strains as a function of the forming conditions like local radii, lubrication, friction, and of course part geometry. These strains are essentially independent of the chosen metal grade and thickness. Plotting these strains allows for a relative assessment of which strains are higher than others, but no judgment can be made on “how high is too high?”
- The Forming Limit Diagram is a combination of the Forming Limit Curve (a material property) and the strains (reflecting part geometry and forming conditions). The FLD provides guidance on which areas of the formed part requires additional attention to achieve robust stamping conditions. Creating a subsequent FLD may be warranted when conditions change, since changes to the sheet metal properties (FLC) and the forming conditions (radii, lubrication, beads, blank size) will change the FLD, potentially affecting the conclusions.
Key Points
-
- Conventional Forming Limit Curves characterize necking failure only. Fractures at cut edges and tight bends may occur at strains lower than that suggested by the Forming Limit Curve.
- Differences in determination and interpretation of FLCs exist in different regions of the world.
- This system of FLCs commonly used for low strength and conventional HSLA is generally applicable to experimental FLCs obtained for DP steels for global formability.
- The left side of the FLC (negative minor strains) is in good agreement with experimental data for DP and TRIP steels. The left side depicts a constant thinning strain as a forming limit.
- Determination of FLCs for TRIP, MS, TWIP, and other special steels typically requires an experimental approach, since conventional simple equations do not accurately reflect the forming limits for these advanced microstructures.
Back to the Top
Formability
A Forming Limit Curve (FLC) is a map of strains indicating the onset of critical through-thickness necking for different linear strain paths. The FLC is dependent on the metal grade and the specific methods used in its creation. When paired with the strains generated during forming of an engineered part, the associated Forming Limit Diagram (FLD) provides guidance on which areas of the part might be prone to necking failures during production stamping conditions that replicate those used in the analysis.
Several methods are available to measure the strains on formed parts. The earliest method is known as Circle Grid Strain Analysis (CGSA), with Dr. Stuart Keeler as its primary evangelist for nearly 50 years. Dr. Keeler was the Technical Editor of these AHSS Guidelines through Version 6.0, released in 2017.
As the name suggests, a flat blank is covered with a grid of circles of precisely known diameter, typically applied by electrochemical etching. Forming turns the circles into ellipses, with the dimensions related to the major and minor strains. Conventional measurement occurs after forming, and involves a calibrated Mylar™ strip marked with gradations indicating the expansion or contraction relative to the initial circle diameter. Typically, these are viewed through magnifiers, making it easier to discern the critical dimensional differences. Techniques and caveats are highlighted in Citations S-59 and S-60.
Instead of circles, most camera-based measurement techniques for analysis after forming use a regular grid pattern of squares or dots. Forming turns the squares into rectangles, and the camera/computer measures the expansion or contraction of the nodes at the corners of the squares to determine the strains. Similarly, forming changes the regular dot pattern, allowing for calculation of the strains.
These approaches determine only the strains after forming, and are constrained to assume linear strain paths. An alternate approach based on Digital Image Correlation (DIC), where a camera tracks the movement of a random speckle pattern applied prior to forming,W-26, H-22, M-21 follows the strain evolution which occurs during forming and is not affected by non-linear strain paths.
Although DIC strain analysis is more accurate and informative, it is a higher-cost approach best suited for laboratory environments. Circle-grid, square-grid, and dot-grid strain analysis are all lower cost options and readily applied on the shop floor. Each of these in-plant techniques have different merits and challenges, including ease of use, accuracy, and cost.
![Crash Management]()
Forming
Introduction
Approaches for forming higher strength steels evolved with the commercialization of increased strength levels of High Strength Low Alloy (HSLA) steels. Demands for greater crash performance while simultaneously reducing mass and cost have spawned the development of new groups of steels that improve on the properties of these HSLA steels. Forming of Advanced High-Strength Steel (AHSS) is not a radical change from forming conventional HSLA steels, providing some of the key differences are understood and accounted for in die design, die process, and equipment selection.
AHSS grades solve two distinct automotive needs by two different groups of steels. The first group as a class has higher strength levels with improved formability and crash-energy absorption compared to HSLA grades. DP, TRIP, FB, and TWIP steels, which have increased values of the work hardening exponent (n-value), fulfill this requirement. The second group, including CP and MS steels, extends the availability of steel in strength ranges above what is available with HSLA grades. Originally targeted for chassis, suspension, and body-in-white components, AHSS grades are now being applied to doors and other body panels. New variations in microstructure help meet specific process requirements, including increased edge stretch, bendability, strengthening after forming, or tighter property tolerances.
The progressive increases in yield and tensile strength with these new AHSS grades magnifies existing forming issues with conventional HSLA grades and creates new challenges. Concerns include higher loads on processing equipment including presses, levelers, straighteners, blanking lines, coil slitting lines and roll forming equipment. Additionally, there are material and surface treatment considerations required for tooling in the stamping plants: draw dies, trim steels, and flange steels. Compared to conventional HSLA steels, greater energy requirements result from higher AHSS yield strengths, tensile strengths and significantly higher work hardening rates. This places new requirements on press capacity, leveler, straightener and slitting capabilities, tool construction/protection, lubricant capabilities, part and process design, and maintenance. Springback management becomes more critical as yield strengths continue to increase. Conventional and press hardened (hot formed) AHSS parts have very high strength after forming, so re- forming operations should be avoided. Trimming, cutting, and piercing equipment must be constructed and maintained to overcome the extreme high strength of the final stamping. Laser cutting of press hardened parts produces a finished part that avoids pushing the limits of trim and pierce tools and dies utilized for conventional HSLA steel.
There are an ever-increasing number of AHSS multiphase microstructure grades available, each designed to resist various forming failure modes while achieving final part performance requirements. Sharing of information regarding the planned part geometry, die and stamping processing, and final part application between steel suppliers, product and die process engineering, and end users helps ensure selection of the right steel grade for the application. This becomes especially relevant since multiphase microstructures experience additional forming failure modes compared with conventional high strength products.
Tool Design Considerations
The characteristics associated with different AHSS grades influence die design and die processing decisions. Not only are these steels typically higher in strength, but they also undergo substantial work hardening during forming. These lead to increased local loads, and changes in friction, die wear, and press requirements. The multiphase microstructures increase cut edge and bending fracture sensitivity. As such, extending the life and performance of tooling in press shops requires a rethinking of tool and part design.
Part Design
Successful application of any material requires close coordination of part design and the manufacturing process. Consult product and manufacturing process engineers when designing AHSS parts to understand both the limitations and advantages of the grade and the proper forming process to be employed. Start in the concept and feasibility stage to ensure sufficient time for corrective actions and optimization.
Soft tool materials like kirksite may be used for manufacturing prototype parts and the inserts used to eliminate local wrinkles or buckles. However, wear resistant coatings are typically not applied to these tool surfaces, so the metal flow seen in these prototype parts may not match the metal flow seen under production conditions. The results from soft tool tryouts should not be used to assess manufacturability and springback of AHSS parts.
Design structural frames (such as rails, sills, cross members, and roof bows) as open-ended channels to permit forming operations rather than draw die processes. AHSS stampings requiring closed-end draw operations are limited by a reduced depth of draw, Figure 1. Less complex, open-ended stamped channels are less limited in depth. A rule of thumb is that DP 350Y600T can be formed to only half the draw depth of a mild steel.

Figure 1: Schematic of an open end part design (left) and a closed end part design (right). The open-ended design allows for greater depths when utilizing AHSS versus the closed ended design historically used with mild steel.A-5
Where possible, avoid closed-end developments to make more complex geometries with AHSS grades. Wrapping ends of “hat” sections increases forming loads, increases the chances of circumferential compression wrinkling on the binder, specifically in the corners, and increases wrinkling on the draw wall if the blank edge runs through the draw bead. Draw die developments that include a closed (or wrapped) end development usually also require a larger blank size. During draw die development, it is best to identify parts that have a “hat” section geometry in certain locations and develop the draw die accordingly to maximize the positive formability attributes of AHSS while minimizing the limitations of AHSS.
For example, the left image in Figure 2 shows a draw die development on a DP600 cowl side with a closed (wrapped) end, with the right image showing a similar part developed with an open end. Although both final part geometries are similar, the closed-end development led to significant global formability failures due to the excessive stretch. In contrast, the open-ended development had virtually no global formability related failures. Other design and die development differences in the part on the right include the use of stake beads to control springback and embossments to eliminate wavy metal. In addition, an open-ended development has the potential to reduce the blank size for material utilization savings.

Figure 2: Draw die development for a cowl side formed from DP600. Left image: closed-end development with global formability failures, waviness, and springback. Right image: open-ended development with no splits, waves, or dimensional concerns.U-6
The automotive industry has adopted a strategy for “lighter dies and fewer dies”, to reduce cost. One key element is “part consolidation”, such as one-piece body side outers and inners. High strength steels challenge the part consolidation mantra. When encountering extreme formability challenges, parts previously made with one set of dies when stamped from lower strength steels may benefit from transitioning to a laser welded blank with a lower strength grade in the challenging region and higher strength steels in the remainder of the part. Alternatively, splitting the consolidated part into two or more separate parts subsequently welded together may improve stamping success at the expense of another operation. In the past, one-piece rocker panels were stamped from conventional mild or HSLA steel. However, this component requires higher strength and reduced thickness to meet weight and crash requirements, so now DP980 is often considered as the grade of choice for this application. Figure 3 shows a rocker panel where insufficient formability of DP980 prevented a one-piece stamping. The OEM solved this by dividing the part into two stampings, putting a more formable grade where needed on the wrapped (or closed) end.

Figure 3: When a one-piece rocker panel could not be successfully formed from DP980, the OEM stamped a DP980 rocker panel section with an open-ended design and spot welded it to a mild steel end cap.U-6
Trim and Pierce Tool Design
- Trim and pierce tools need to withstand higher loads since AHSS grades have higher tensile strengths than conventional high-strength steels.
- Edge cracking is minimized with proper support of the trim stock during trimming.
- Modify timing of the trim/pierce operation to minimize snap-through reverse loading.
- Scrap shedding may be an issue, since AHSS springback can cause scrap to stick in the tool.
Flange Design
- Design more formable flanges to reduce need for extra re-strike operations.
- Areas to be flanged should have a “break-line” or initial bend radius drawn in the first die to reduce springback.
- Adapt die radii for material strength and blank thickness.
Draw Bead Design
- Metal flow across draw beads generates strain and minimizes the elastic recovery which causes springback.
- Metal flow across draw beads generates large amounts of work hardening, leading to increased press loads.
- Optimizing blank size and shape reduces the reliance on draw beads, which can excessively work harden the material before entering the die opening.
Guidelines to Avoid Edge Cracking During Stretch Flanging
- Flange length transition should be gradual – abrupt changes in flange length cause local stress raisers leading to edge cracks.
- Use good cutting practices to achieve a high-quality edge.
- Avoid the use of sharp notch features in curved flanges.
- Avoid putting bypass notches in stretch or compression edges of blanks or progressive die carrier strips. These bypass notches can act as stress risers and lead to edge fractures in the draw or flange operation. In addition, bypass notches in blanks and progressive dies are difficult to maintain, which can increase the potential for edge fracture.
- Metal gainers in the draw die or in the die prior to the stretch flange operation compensates for change in length of line that occurs during flanging, helping to avoid edge cracking. In the example shown in Figure 4, edge fractures moved from the draw panel to flanged panel after grinding on the draw die to eliminate edge fractures in the draw operation. The draw panel underneath the flanged part in Figure 4 did not have edge fractures. The reduction in the length of line in the draw operation moved the problem to the flanged part where the stamping transitioned from bending and straightening in the flange operation to a stretch flange operation. A better practice is to add metal gainers to the draw panel to provide the feedstock which expands during stretch flanging.

Figure 4: Flanged panel fractures, with the draw panel underneath. Adding metal gainers to the draw panel would help minimize these fractures.U-6
- The higher strength of AHSS makes it more difficult to pull out loose metal or achieve a minimum stretch in flat sections of stampings. Addendum, metal gainers (Figures 5 and 6), and other tool features balance lengths of line and locally increase stretch.

Figure 5: Metal gainers help avoid insufficient stretched areas and eliminate buckles.T-3

Figure 6: Metal gainers and depressions balance stresses and minimizes wrinkled metal.A-41
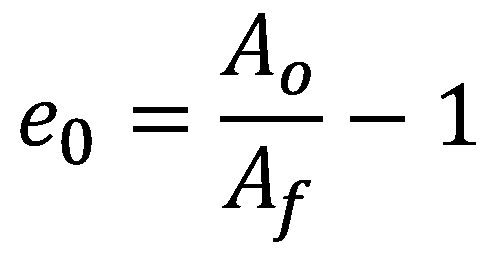



![Figure 8: Close-up views of Location 1 (left) and Location 2 (right) identified in Figure 7 [material: 980DP(LSi)]; Location 1 is a pierced hole that was extruded during forming, and Location 2 is a blanked perimetric edge that was stretched during forming (underside with respect to Figure 7). H-15](https://ahssinsights.org/wp-content/uploads/2020/10/2.3.5-Fig8.jpg)