Joining, Laser Welding
In this study by Shanghai Jiao Tong University and General Motors Company on liquid metal Embrittlement (LME)Z-11, hot dipped 1.2mm galvanized QP980 steel sheets with a 6 micron thick zinc rich coating on top of a 2 micron thick transition zone to the base metal were used. The laser welder is tilted 5º ahead of weld pool to avoid back reflection. The welding velocity was varied from 4-6 m/min and laser power from 4-6.5 kW. Referencing Table 1, Schedules #1–4 were intended to investigate effects of laser power on LME cracks using 6 m/min. schedules #4–6 varied velocity with the laser power staying constant at 4.5 kW. In addition, schedules #6 and #7 varied laser power at a relatively lower welding velocity of 4 m/min.
Table 1: Process Parameters.Z-11
Full penetration welds did not result in cracking while partial penetration welds with lower energy density did. The lowest energy density welds resulted in no cracking but the penetration was barely beyond the faying surface. Cracks resembles an inverse “Y” where the cracks initiated at the faying surface and propagated along the direction of solidification towards the weld centerline. Cracks at notch root were wider than centerline crack indicating grain boundary separation. The fracture method is characteristic of quasi-cleavage indicating that the grain boundaries were embrittled by Fe-Zn intermetallics. Crack initiation at the faying surface can be explained by the residual stresses that form highest at the faying surface during cooling. This stress concentration is eliminated with full penetration weld pass as well as in wide and shallow passes as seen in Figure 1.
Figure 1: Von Mises Stress Distribution.Z-11
Because the process of laser welding is so short, the vaporized zinc and intermetallics do not have time to outgas completely. The liquid zinc diffuses along the austenite grain boundaries and stabilize ferrite given ferrite has a higher solubility of Zn compared to austenite. The remaining liquid Zn reacts with the ferrite to form the solid Γ-Fe3Zn10 which is a hard brittle intermetallic that can easily induce cracking. Another peritectic reaction occurs with Γ-Fe3Zn10 and liquid zinc forming another brittle intermetallic δ-FeZn10. The stabilized ferrite and intermetallics occur before austenite transform to martensite and remains even after this reaction occurs.
The formation of the intermetallics between the grain boundaries decreases ductility and with the combination of the high residual stress and stress concentration at the faying surface, the crack initiates and propagates. The cracking follows the grain growth to the center of the weld. Liquid Zn accumulates at the center of the weld and results in Fe-Zn intermetallics with low ductility that can eventually propagate cracking that occurs at the edge of the weld. Welds that result in a smaller cross-sectional area on the faying surface benefit from the reduction in vaporized Zn that cannot be outgassed while full penetration welds with keyhole mode can allow Zn to out gas from both the top and bottom of the weld as well as increased nugget size decreasing the Zn concentration to where brittle Fe-Zn phases do not form. Full penetration welds are recommended to reduce residual stress as well as allow sufficient outgassing of vaporized Zn in the weld pool.
Figure 2: LME illustration.Z-11
Figure 3: Zn diffusion.Z-11
Summary
LME cracks initiated at the weld notch root on the faying surface and propagated towards the center of the weld along the direction of columnar growth. Brittle intermetallic help induce cracking in the weld metal in addition to restraint from the weld joint. Full penetration welds were found to reduce Zn content from the weld in addition to reducing restraint as compared to partial penetration welds. The full penetration weld allowed for zinc to be outgassed from the weld on both sides reducing the Zn content in the weld to an acceptable level. Full penetration welds also reduced the residual stresses that formed during partial penetration welds due to the restraint on the root side of the weld.
![Fatigue]()
structural performance
Normal vehicle use leads to repeated loading of components and joints. Stress concentrations in the body structure may lead to plastic strains at stresses below the yield strength due to cyclic fatigue. Conventional High-Strength Steel fatigue behavior correlates with their tensile strength. However, in multiphase steels, the strain distribution between phases within the steel microstructure affects the fatigue response, leading to a different response depending on which phases accommodate the strain.
The fatigue strength of DP steels is higher than that of precipitation-hardened steels or fully bainitic steels of similar yield strength for several metallurgical reasons. The dispersed fine martensite particles retard the propagation of fatigue cracks. For TRIP steels, the transformation of retained austenite can relax the stress field and introduce a compressive stress that can also improve fatigue strength. General categorization may not be possible – studies have reported cyclic hardening occurs in Dual Phase steels where the martensite volume fraction is less than 0.5 while Dual Phase steels at higher martensite content (higher strength) soften under cyclic loading conditions. C-15, W-27 Furthermore, fatigue limits are complicated by environmental factors like the presence of hydrogen.
Figures 1 and 2 illustrate the general improvements in fatigue capability offered by Advanced High-Strength Steel (AHSS) grades.
Figure 1: Fatigue characteristics of TRIP steel CR450Y780T-TR compared to conventional steels.T-24
Figure 2: Fatigue limit for AHSS compared to conventional steels.T-2
The table below lists some fatigue properties for conventional and advanced high strength steels.
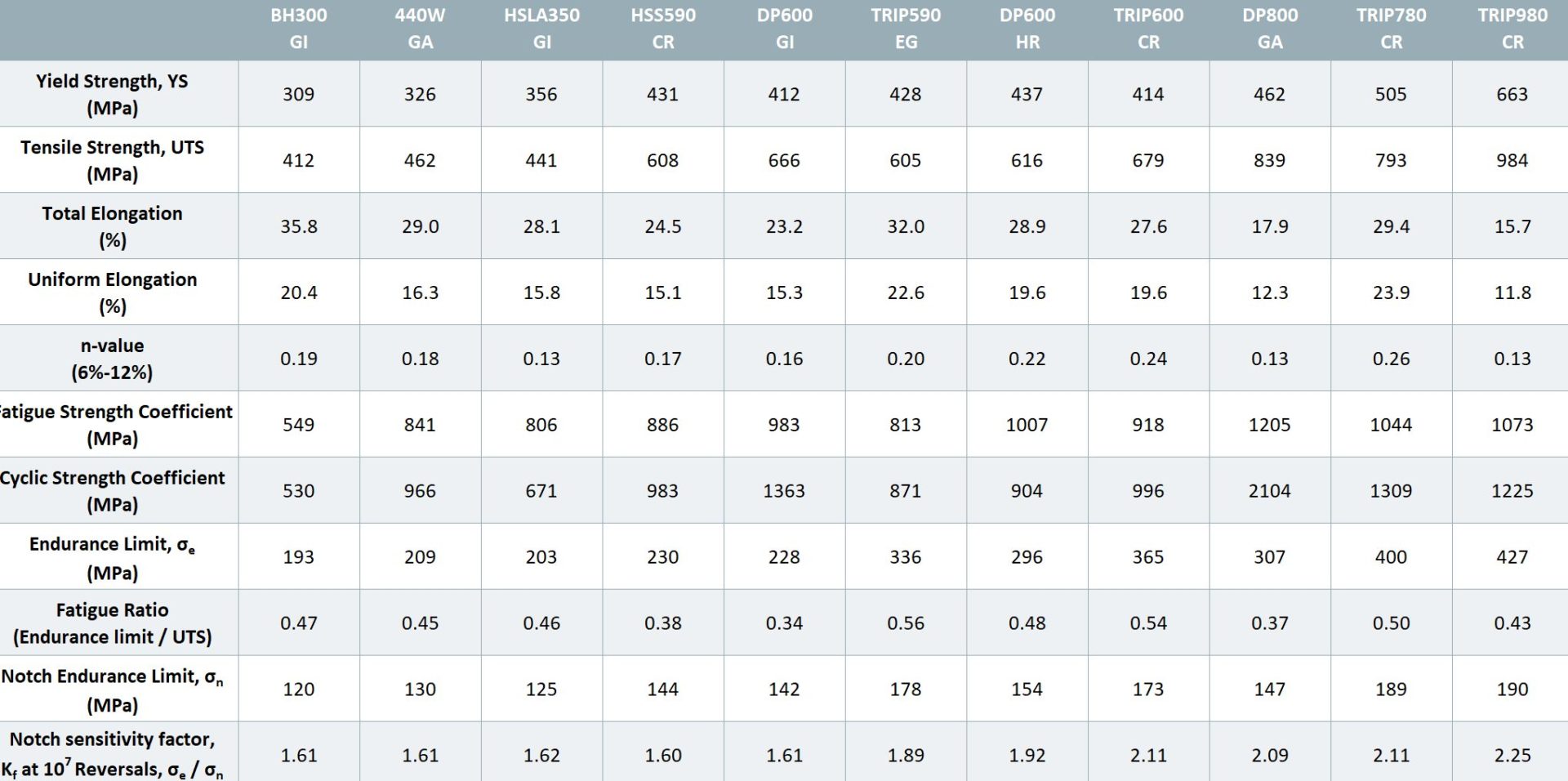
Table 1: Fatigue properties for HSS and AHSS grades Y-11
Formability
Strength is defined as load divided by cross-sectional area. In a tensile test, the choice of when the cross-sectional area is measured influences the results.
It is easiest to measure the width and thickness of the test sample before starting the pull. At any load, the engineering stress is the load divided by this initial cross-sectional area. Engineering stress reaches a maximum at the Tensile Strength, which occurs at an engineering strain equal to Uniform Elongation. After that point, engineering stress decreases with increasing strain, progressing until the sample fractures.
However, metals get stronger with deformation through a process known as strain hardening or work hardening. As a tensile test progresses, additional load must be applied to achieve further deformation, even after the “ultimate” tensile strength is reached. Understanding true stress and true strain helps to address the need for additional load after the peak strength is reached.
During the tensile test, the width and thickness shrink as the length of the test sample increases. Although these dimensional changes are not considered in determining the engineering stress, they are of primary importance when determining true stress. At any load, the true stress is the load divided by the cross-sectional area at that instant.
The true stress – true strain curve gives an accurate view of the stress-strain relationship, one where the stress is not dropping after exceeding the tensile strength stress level.
- True stress is determined by dividing the tensile load by the instantaneous area.
- True strain is the natural logarithm of the ratio of the instantaneous gauge length to the original gauge length.
True stress – true strain curves of low carbon steel can be approximated by the Holloman relationship:
σ = Kεn
where true stress = σ; true strain = ε, n is the n-value (work hardening exponent or strain hardening exponent), and the K-value is the true stress at a true strain value of 1.0 (called the Strength Coefficient).
True stress-strain curves obtained from tensile bars are valid only through uniform elongation due to the effects of necking and the associated strain state on the calculations. Inaccuracies are introduced if the true stress-true strain curve is extrapolated beyond uniform strain, and as such a different test is needed. Biaxial bulge testing has been used to determine stress-strain curves beyond uniform elongation. Optical measuring systems based on the principles of Digital Image Correlation (DIC) are used to measure strains. The method by which this test is performed is covered in ISO 16808.I-12
Stress-strain curves and associated parameters historically were based on engineering units, since starting dimensions are easily measured and incorporated into the calculations. True stress and true strain provide a much better representation of how the material behaves as it is being deformed, which explains its use in computer forming and crash simulations. Although sample dimensions are challenging to measure during a tensile test, there are equations that relate engineering units to true units. Conventional stress-strain curves generated in engineering units can be converted to true units for inclusion in simulation software packages.
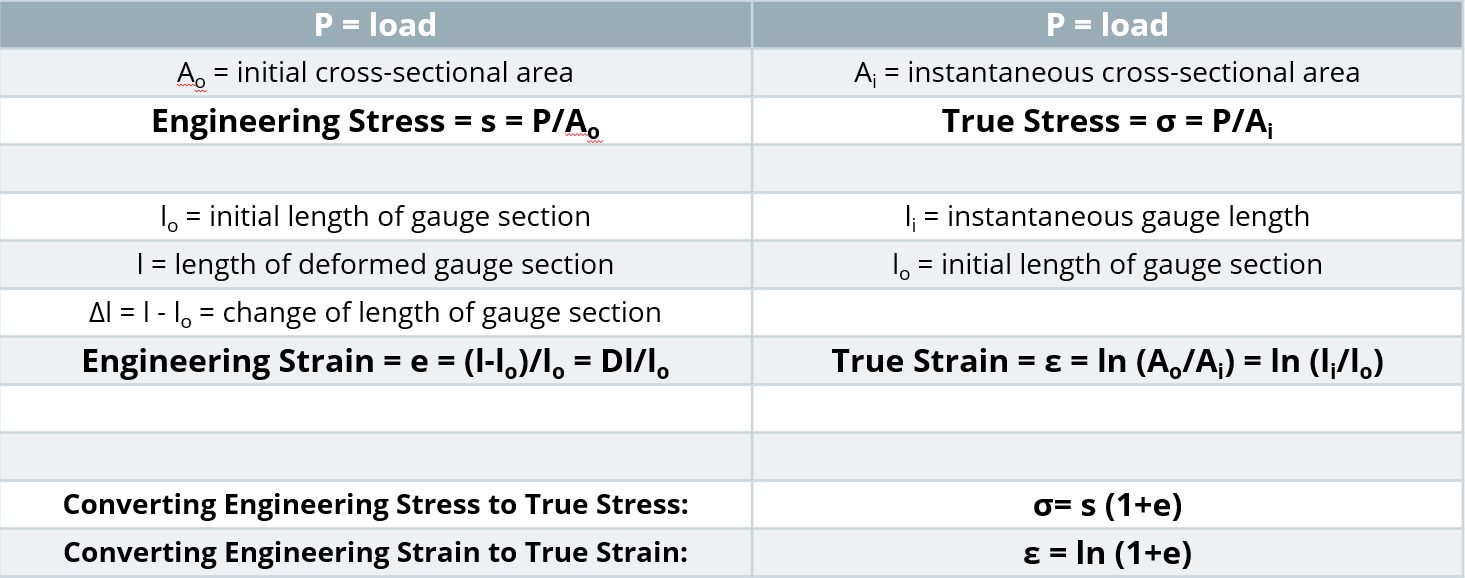
Relationships Between Engineering and True Properties
