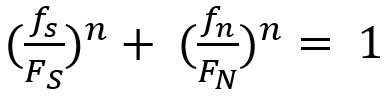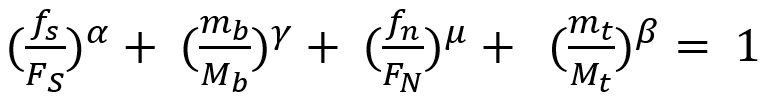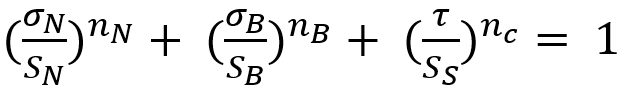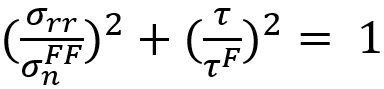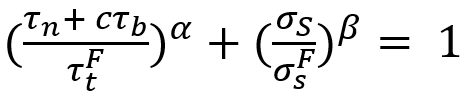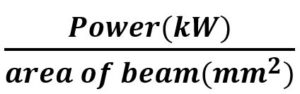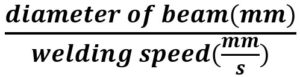Blog, main-blog, RSW Modelling and Performance
Modelling resistance spot welding can help to understand the process and drive innovation by asking the right questions and giving new viewpoints outside of limited experimental trials. The models can calculate industrial-scale automotive assemblies and allow visualization of the highly dynamic interplay between mechanical forces, electrical currents and thermal flow during welding. Applications of such models allow efficient weldability tests necessary for new material-thickness combinations, thus well-suited for applications involving Advanced High -Strength Steels (AHSS).
Virtual resistance spot weld tests can narrow down the parameter space and reduce the amount of experiments, material consumed as well as personnel- and machine- time. They can also highlight necessary process modifications, for example the greater electrode force required by AHSS, or the impact of hold times and nugget geometry. Other applications are the evaluation of whole-part distortion to ensure good part-clearance and the investigation of stress, strain and temperature as they occur during welding. This more research-focused application is useful to study phenomena arising around the weld such as the formation of unwanted phases or cracks.
Modern Finite-Element resistance spot welding models account for electric heating, mechanical forces and heat flow into the surrounding part and the electrodes. The video shows the simulated temperature in a cross-section for two 1.5 mm DP1000 sheets:
First, the electrodes close and then heat starts to form due to the electric current flow and agglomerates over time. The dark-red area around the sheet-sheet interface represents the molten zone, where the nugget forms after cooling. While the simulated temperature field looks plausible at first glance, the question is how to make sure that the model calculates the physically correct results. To ensure that the simulation is reliable, the user needs to understand how it works and needs to validate the simulation results against experimental tests. In this text, we will discuss which inputs and tests are needed for a basic resistance spot welding model.
At the base of the simulation stands an electro-thermomechanical resistance spot welding model. Today, there are several Finite Element software producers offering pre-made models that facilitate the input and interpretation of the data. First tests in a new software should be conducted with as many known variables as possible, i.e., a commonly used material, a weld with a lot of experimental data available etc.
As first input, a reliable material data set is required for all involved sheets. The data set must include thermal conductivity and capacity, mechanical properties like Young’s modulus, tensile strength, plastic flow behavior and the thermal expansion coefficient, as well as the electrical conductivity. As the material properties change drastically with temperature, temperature dependent data is necessary at least until 800°C. For more commonly used steels, high quality data sets are usually available in the literature or in software databases. For special materials, values for a different material of the same class can be scaled to the respective strength levels. In any case, a few tests should be conducted to make sure that the given material matches the data set. The next Figure shows an exemplary material data set for a DP1000. Most of the values were measured for a DP600 and scaled, but the changes for the thermal and electrical properties within a material class are usually small.
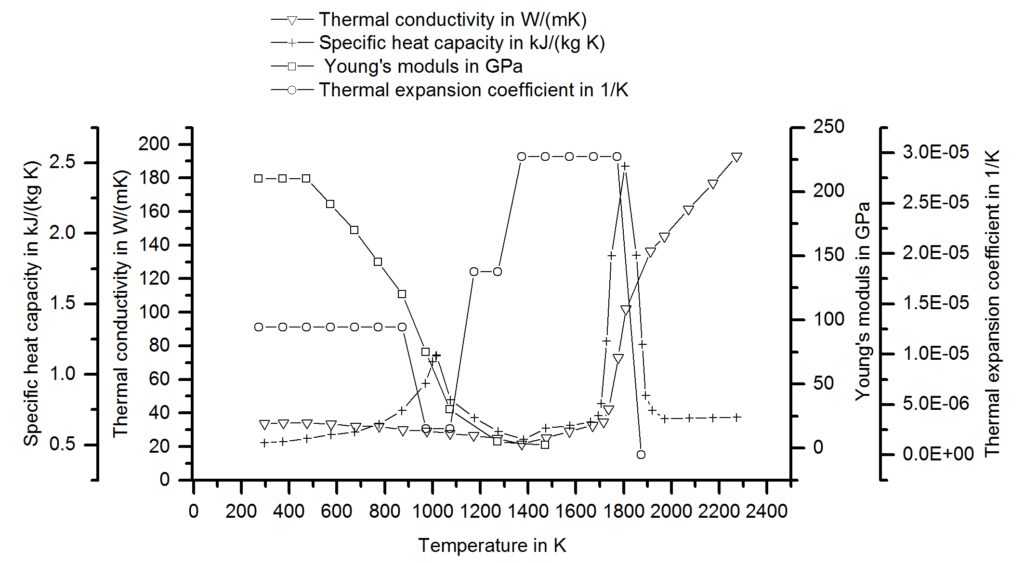
Figure 1: Material Data set for a DP1000.S-73
Next, meaningful boundary conditions must be chosen and validated against experiments. These include both the electrode cooling and the electrical contact resistance. To set up the thermal flow into the electrode, temperature measurements on the surface are common. In the following picture, a measurement with thermocouples during welding and the corresponding result is shown. By adjusting the thermal boundary in the model, the simulated temperatures are adjusted until a good match between simulation and experiment is visible. This calibration needs to be conducted only once when the model is established because the thermal boundary remains relatively constant for different materials and coatings.
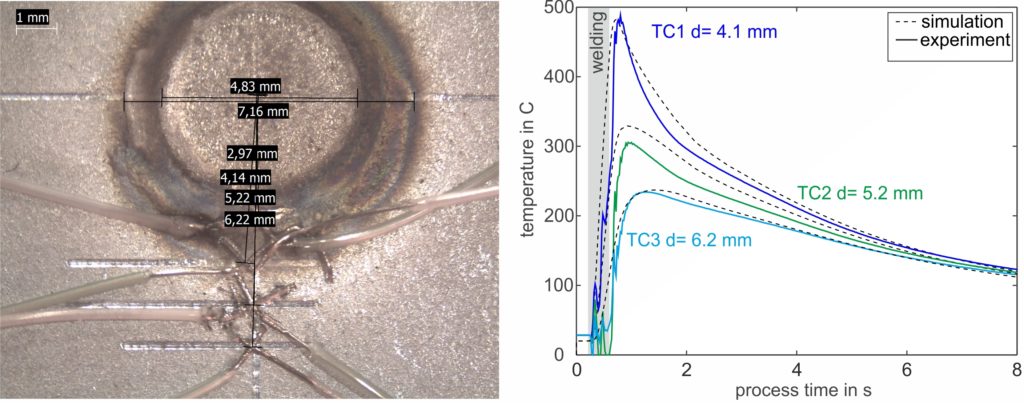
Figure 2: Temperature measurement with thermocouples during welding and the results. The simulated temperature development is compared to the experimental curve and can be adjusted via the boundary conditions.F-23
The second boundary condition is the electrical contact resistance and it is strongly dependent on the coating, the surface quality and the electrode force. It needs to be determined experimentally for every new coating and for as many material thickness combinations as possible. In the measuring protocol, a reference test eliminates the bulk material resistance and allows for the determination of the contact resistances using a µOhm-capable digital multimeter.
Finally, a metallographic cross-section shows whether the nugget size and -shape matches the experiment. The graphic shows a comparison between an actual and simulated cross section with a very small deviation of 0.5 mm in the diameter. As with the temperature measurements, a small deviation is not cause for concern. The experimental measurements also exhibit scatter, and there are a couple of simplifications in the model that will reduce the accuracy but still allow for fast calculation and good evaluation of trends.
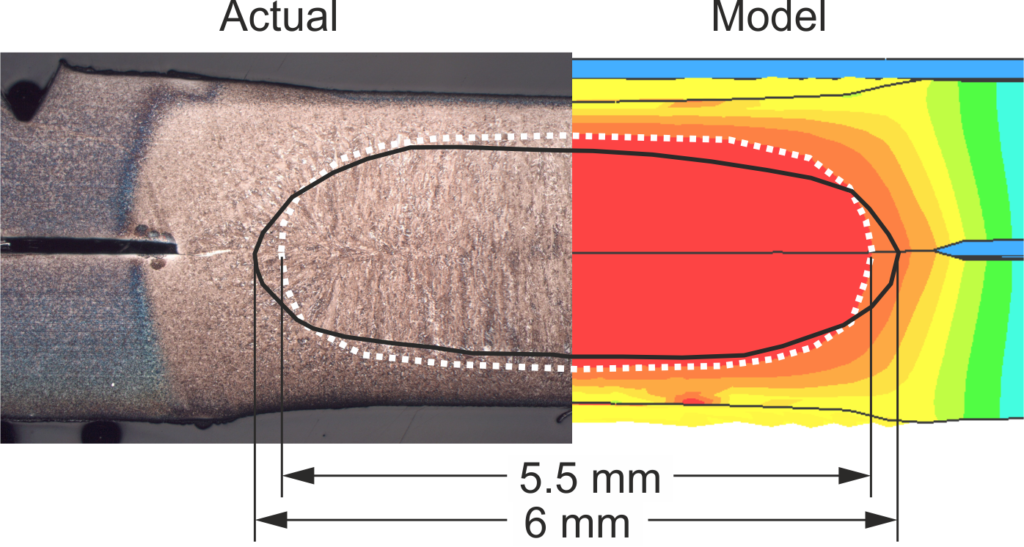
Figure 3: Comparison of experimental and virtual cross-sections.F-23
After validation, consider conducting weldability investigations with the model. Try creating virtual force / current maps and the resulting nugget diameter to generate first guesses for experimental trials. We can also gain a feeling how the quality of each weld is affected by changes in coatings or by heated electrodes when we vary the boundary conditions for contact resistance and electrode cooling. The investigation of large spot-welded assemblies is possible for part fit-up and secondary effects such as shunting. Finally, the in-depth data on temperature flow and mechanical stresses is available for research-oriented investigations, cracking and joint strength impacts.
Note: The work represented in this article is a part a study of Liquid Metal Embrittlement (LME), commissioned by WorldAutoSteel. You can download the free report on the results of the LME study, including how this modelling was used to verify physical tests, from the WorldAutoSteel website.
RSW Modelling and Performance
This article summarizes the findings of a paper entitled, “Prediction of Spot Weld Failure in Automotive Steels,”L-48 authored by J. H. Lim and J.W. Ha, POSCO, as presented at the 12th European LS-DYNA Conference, Koblenz, 2019.
To better predict car crashworthiness it is important to have an accurate prediction of spot weld failure. A new approach for prediction of resistance spot weld failure was proposed by POSCO researchers. This model considers the interaction of normal and bending components and calculating the stress by dividing the load by the area of plug fracture.
Background
Lee, et al.L-49 developed a model to predict spot welding failure under combined loading conditions using the following equation, based upon experimental results .
|
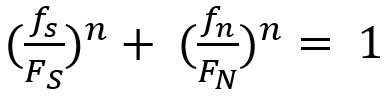Equation 1 |
Where FS and FN are shear and normal failure load, respectively, and n is a shape parameter.
Later, Wung and coworkersW-38 developed a model to predict the failure mode based upon the normal load, shear load, bending and torsion as shown in Equation 2.
 |
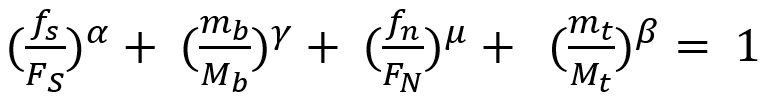Equation 2 |
Here, FS, FN ,Mb and Mt are normal failure load, shear failure load, failure moment and failure torsion of spot weld, respectively. α, β, γ and μ are shape parameters.
Seeger et al.S-106 proposed a model for failure criterion that describes a 3D polynomial failure surface. Spot weld failure occurs if the sum of the components of the normal, bending and shear stresses are above the surface, as shown in the Figure 1.
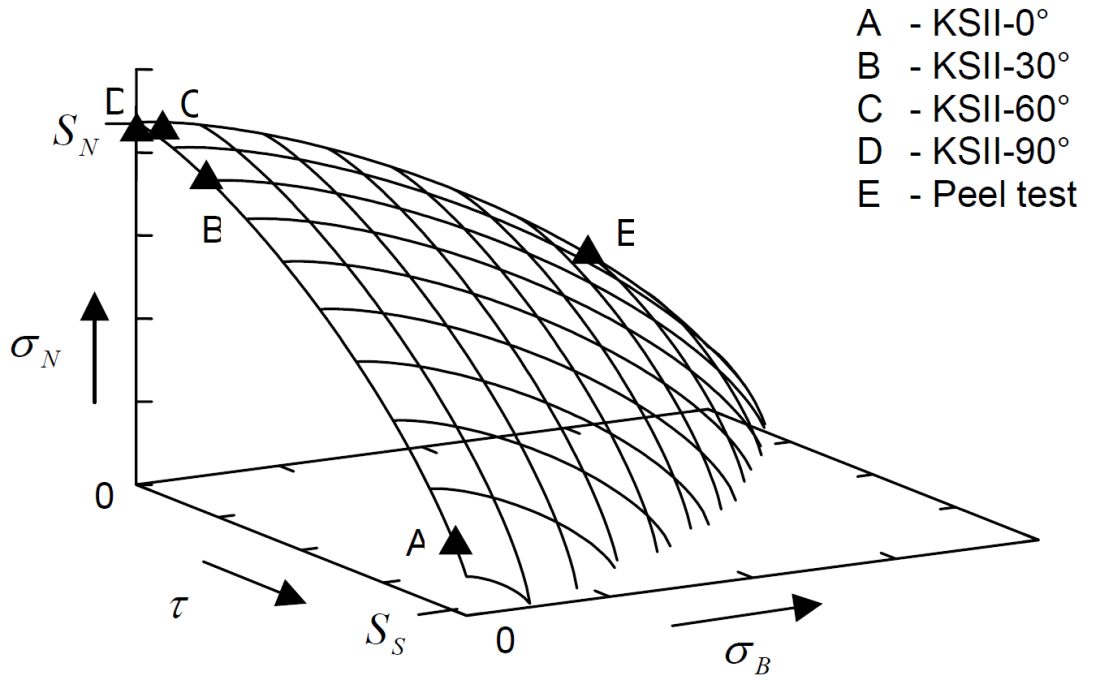
Figure 1: Spot weld failure model proposed by Seeger et al.S-106
The failure criterion can be expressed via Equation 3.
 |
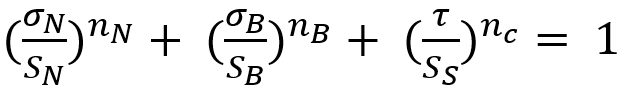Equation 3 |
Here, σN , σB , and τ are normal, bending and shear stress of the spot weld, respectively. And nN, nB and nc are the shape parameters. Toyota Motor CorporationL-50 has developed the stress-based failure model as shown in Equation 4.
 |
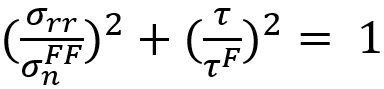Equation 4 |
Hybrid Method to Determine Coefficients for Failure Models
This work used a unique hybrid method to determine the failure coefficients for modeling. The hybrid procedure steps are as follows:
- Failure tests are performed with respect to loading conditions.
- Finite element simulations are performed for each experiment.
- Based on the failure loads obtained in each test, the instant of onset of spot weld failure is determined. Failure loads are extracted comparing experiments with simulations.
- Post processing of those simulations gives the failure load components acting on spot welds such as normal, shear and bending loads.
These failure load components are plotted on the plane consisting of normal, shear and bending axes.
The hybrid method described above is shown in Figure 2.L-48
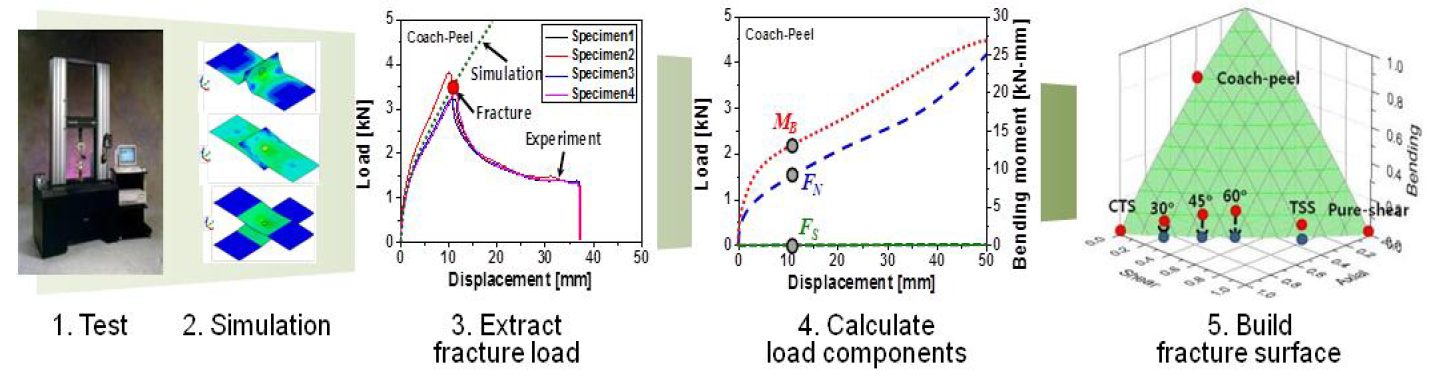
Figure 2: Hybrid method to obtain the failure load with respect to test conditions.L-48
New Spot Weld Failure Model
The new proposed spot weld failure model in this paper considers only plug fracture mode as a normal spot weld failure. Secondly normal and bending components considered to be dependent upon each other. Stress generated by normal and bending components is shear, and shear component generates normal stress. Lastly authors have used πdt to calculate the area of stress instead of πd2/4. The final expression is shown in the Equation 5.
 |
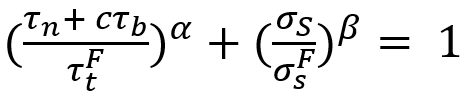Equation 5 |
Here τn is the shear stress by normal load components, σS is the normal stress due to shear load component. And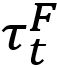 
, 
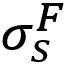, c, α and β are coefficients.
This work included verification experiments of 42 kinds of homogenous steel stack-ups and 23 heterogeneous stack-ups. The strength levels of the steels used was between 270 MPa and 1500 MPa, and thickness between 0.55 mm and 2.3 mm. These experiments were used to evaluate the model and compare the results to the Wung model.
Conclusions
Overall, this new model considers interaction between normal and bending components as they have the same loading direction and plane. The current developed model was compared with the Wung model described above and has shown better results with a desirable error, especially for asymmetric material and thickness.
Joining, Laser Welding, Press Hardened Steels
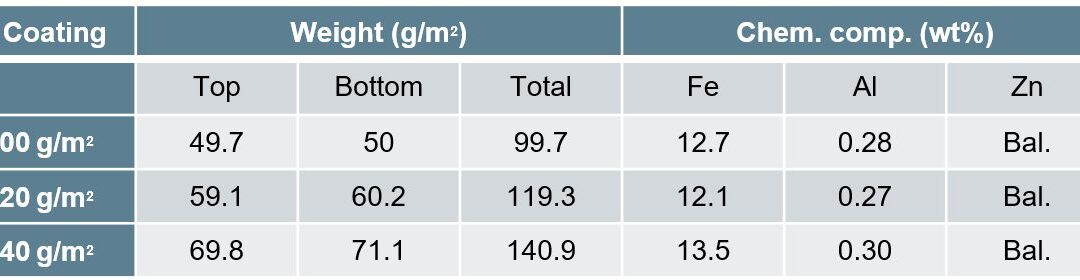
This studyR-25, conducted by the Centre for Advanced Materials Joining, Department of Mechanical & Mechatronics Engineering, University of Waterloo, and ArcelorMittal Global Research, utilized 2mm thick 22MnB5 steel with three different coating thicknesses, given in Table 1. The fiber laser welder used 0.3mm core diameter, 0.6mm spot size, and 200mm beam focal length. The trials were done with a 25° head angle with no shielding gas but high pressure air was applied to protect optics. Welding passes were performed using 3-6kW power increasing by 1 kW and 8-22m/min welding speed increasing by 4m/min. Compared to the base metal composition of mostly ferrite with colonies of pearlite, laser welding created complete martensitic composition in the FZ and fully austenized HAZ while the ICHAZ contained martensite in the intergranular regions where austenization occurred.
Table 1: Galvanneal Coatings.R-25
Figure 1: Base metal microstructure(P=pearlite, F=ferrite, Γ=Fe3Zn10, Γ1=Fe5Zn21 and δ=FeZn10).R-25
Figure 2: Welded microstructure — (a) overall view, (b) HAZ, (c) ICHAZ at low and (d) high magnifications, (e) UCHAZ (f) FZ, and (g) coarse-lath martensitic structure (where M; martensite, P: pearlite, F: ferrite).R-25
Given the lower boiling temperature of Zn at 900 °C as compared to Fe, the interaction of the laser with the Zn plasma that forms upon welding affects energy deliverance and depth of penetration. Lower coating weight of (100 g/m2) resulted in a larger process window as compared to (140 g/m2). Increased coating weight will reduce process window and need higher power and lower speeds in order to achieved proper penetration as shown in Figure 3 and Figure 4. Depth of penetration due to varying welding parameters was developed:
d=(H-8.6+0.08C)/(0.09C-4.8)
[d= depth of penetration(mm), H= heat input per unit thickness(J/mm2), C= coating weight(g/m2)]
Given the reduction in power deliverance, with an increase in coating weight there will be an expected drop in FZ and HAZ width. Regardless of the coating thickness, the HAZ maintained its hardness between BM and FZ. No direct correlation between coating thickness and YS, UTS, and elongation to fracture levels were observed. This is mainly due to the failure location being in the BM.
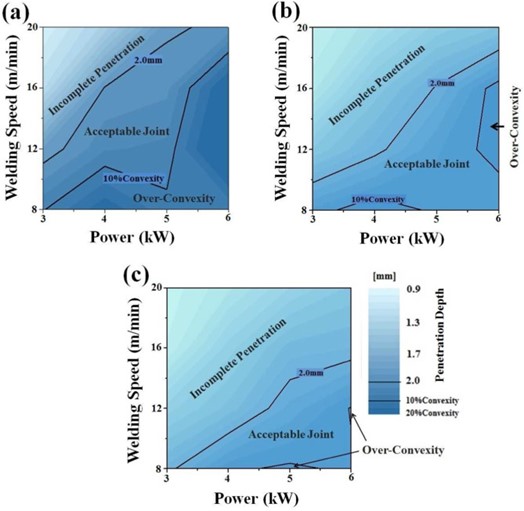
Figure 3: Process map of the welding window at coating weight of (a) 100 g/m2, (b) 120 g/m2, and (c) 140 g/m2.R-25
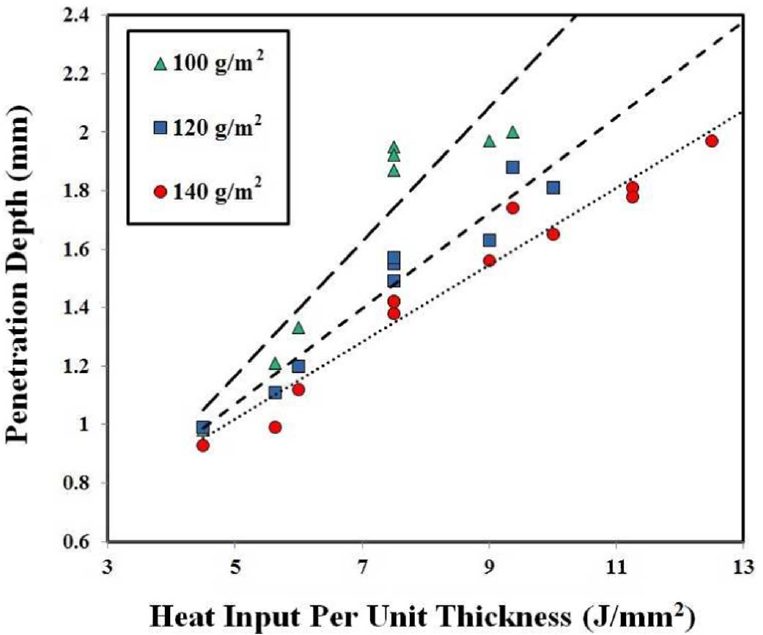
Figure 4: Heat input per unit thickness vs depth of penetration.R-25
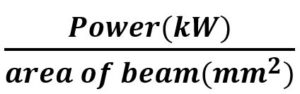
Joining Dissimilar Materials, Laser Welding
Given the use of many different metals in the Body in White construction, it is important to understand the effects of dissimilar welding AHSS. Researchers at Indian Institute of Technology Madras in Chennai, India and Centre of Laser Processing of Materials in Hyderabad, India developed tests to study the resulting microstructure from laser welding 2.5 mm thick DP600 steel to 3 mm thick AA6061 aluminium alloy using a laser beam diameter of 1.5 mm.I-1 They discovered a softening in the steel HAZ due to a tempering effect and an increase in hardness in the aluminum HAZ due to the presence of aluminium intermetallic phases present. Maximum shear strength was observed when the thickness of intermetallics was reduced to 8-11 microns. They concluded that best quality welds were made under power densities and interaction times of 1.98kW/mm2, 0.15s and 2.26 kW/mm2, 0.187s.
The laser power was varied from 3 kW to 4.5 kW and the scanning speed of 8 mm/s, 10 mm/s, and 12 mm/s. Power density and interaction time were two parameters they used to compare trials where:
| Power density (Pd) = |
|
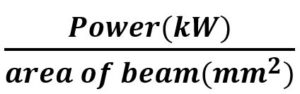and
| interaction time (It) = |
 |
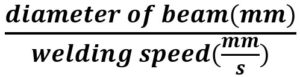The resulting welding parameters are shown in Table 1 below. Figure 1 shows the microstructure of the fusion boundary and HAZ on the DP600 side of the welded joint. Figure 2 shows the microstructure of the weld interface on the AA 6061 side. Figure 3 displays the hardness data with (a) representing 3.5 kW and 10 mm/s, (b) representing 3.5 kW and 8 mm/s, and (c) representing 4 kW and 8 mm/s. Figure 4 represents the Shear Stress-Strain of the welds given different IMC thickness.
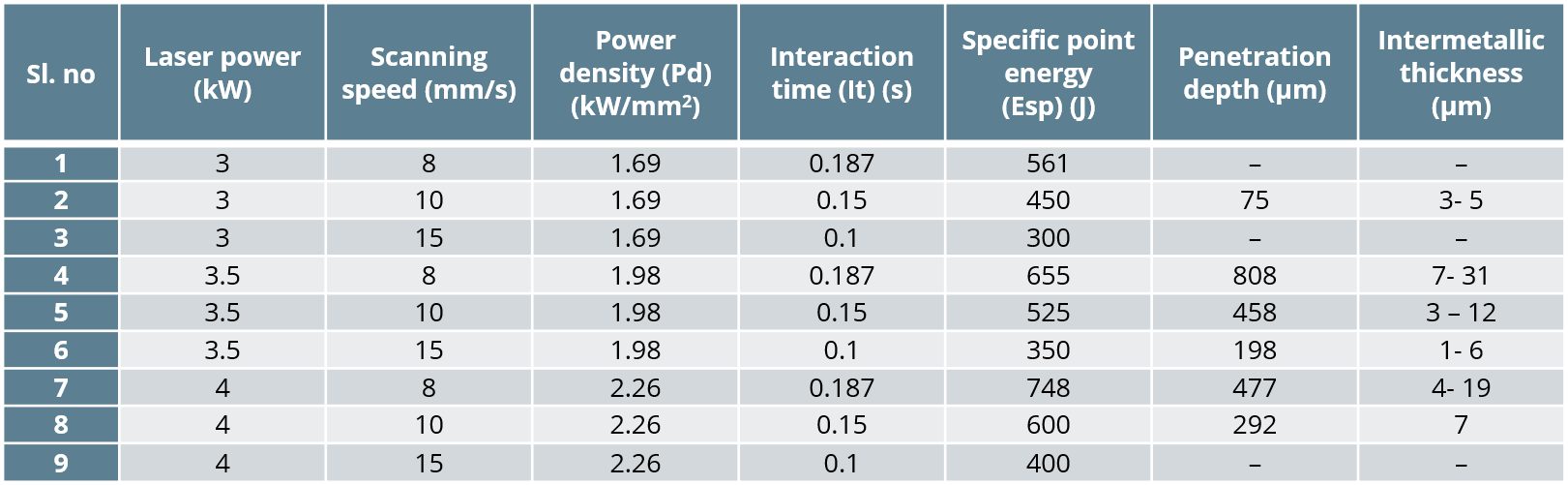
Table 1: Welding Parameters.I-1
Figure 1: Weld Metal, DP 600 Base Metal and HAZ microstructure.I-1
Figure 2: Fe-Al interface microstructure.I-1
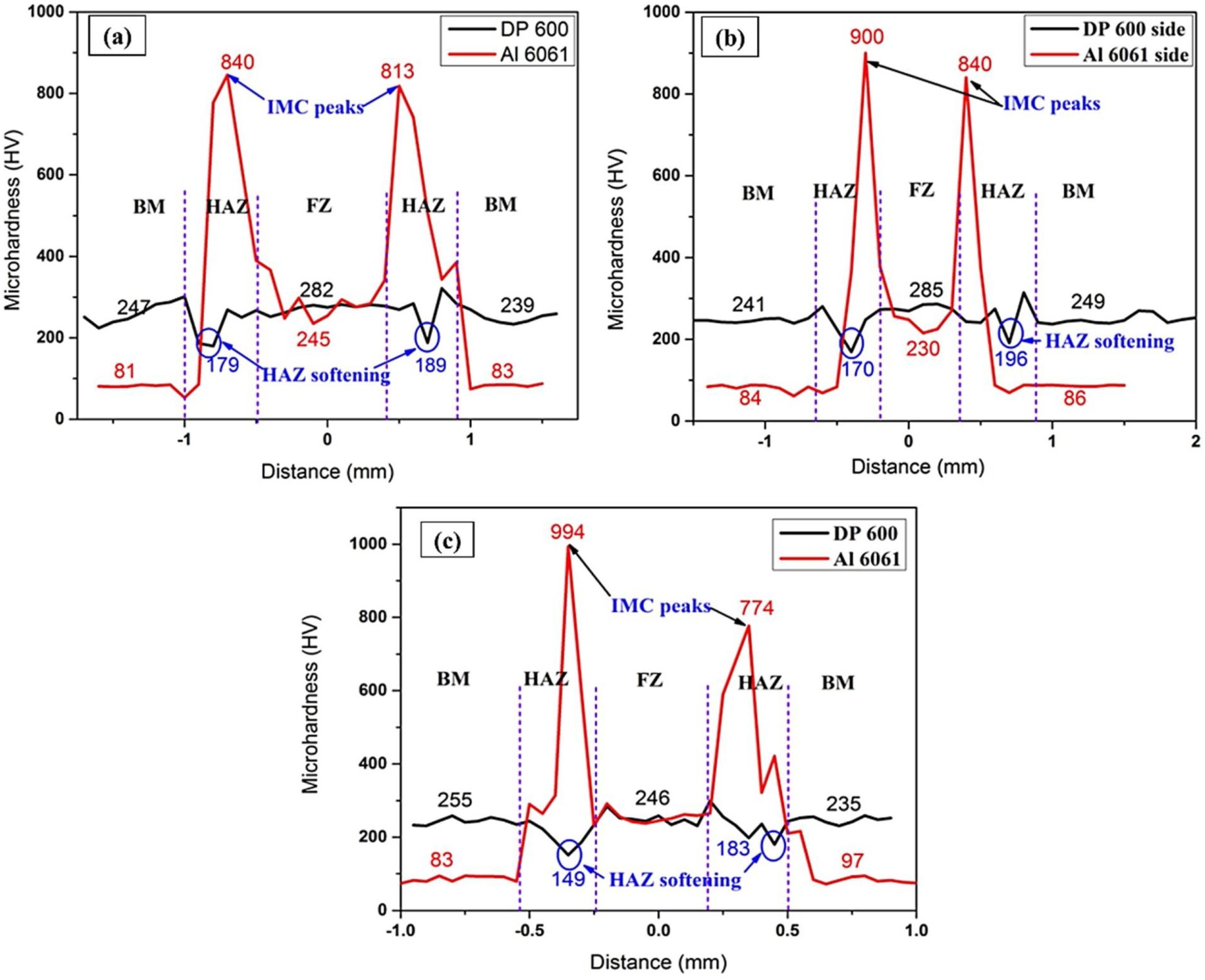
Figure 3: Microhardness Plot.I-1
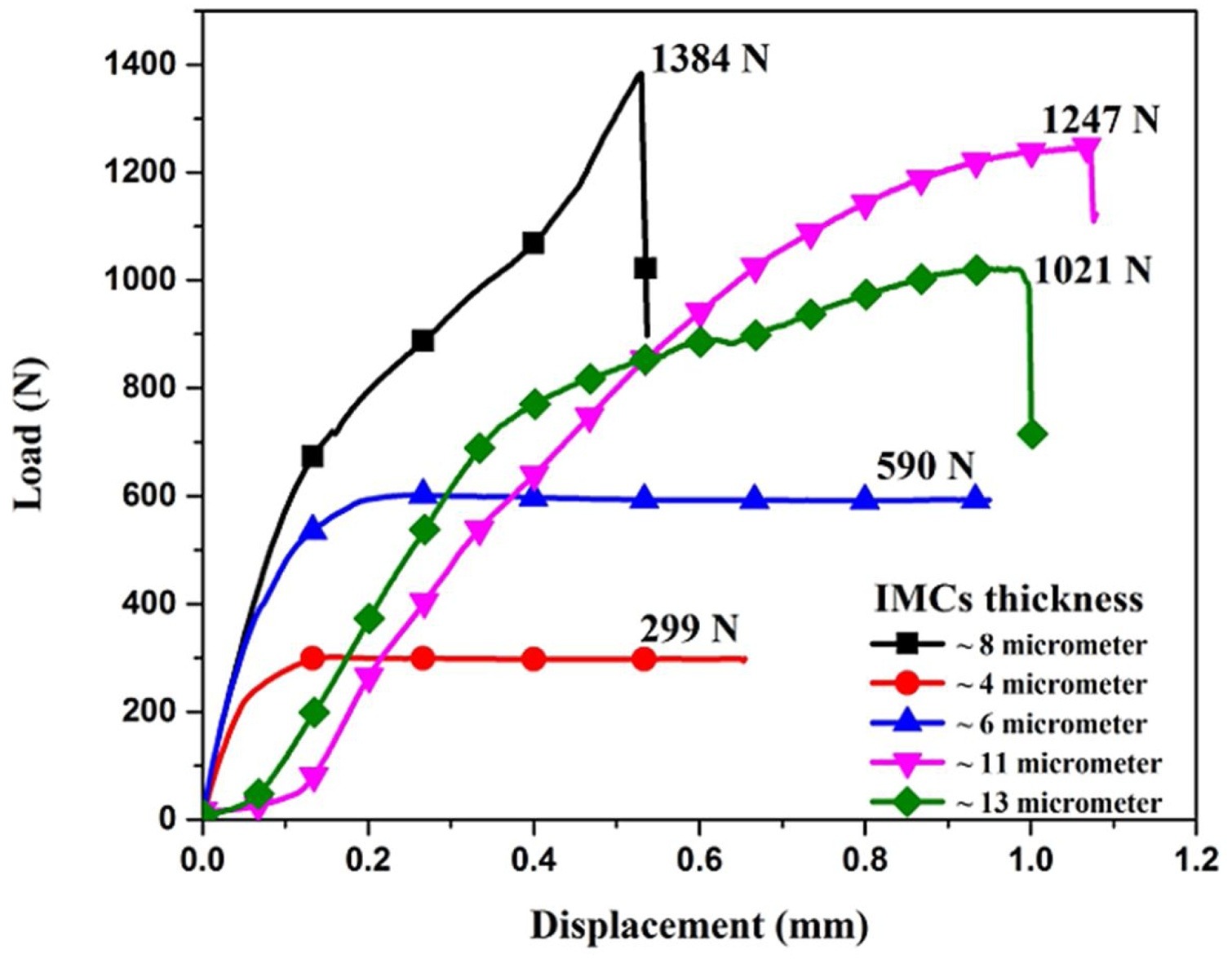
Figure 4: Load vs. Displacement.I-1
Arc Welding, Joining
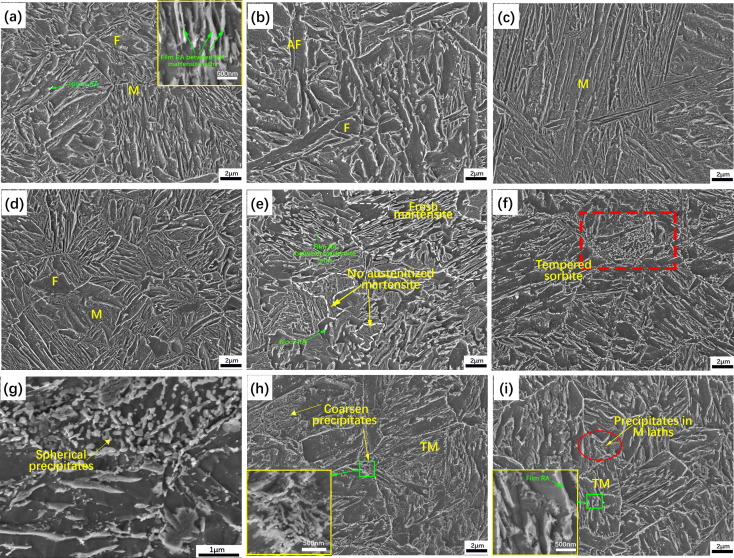
Quenching and partitioning (QP) steels are one of several third generation advanced high strength steel formed by controlled martensite phase fractions and retained austenite. Researchers from the University of Shanghai Jiao Tong tested the effect of HAZ softening in a QP1180 lap joint with the GMAW cold metal transfer (CMT) process.W-1 The steel was welded with ER130s electrode. The fusion zone consisted of chiefly acicular ferrite. The supercritical zone consists of martensite, which is harder than the base metal. There is a drop in hardness (100 HV) in the subcritical zone, and there is a noted lack of retained austenite present in the microstructure. Precipitates are also present in the subcritical zone. The intercritical HAZ only experiences mild softening; where fresh martensite has formed. The softening in the subcritical HAZ presents room for failure that must be accounted for when planning welding using CMT.
Figure 1 shows the different microstructures in detail throughout the weld and the base metal. In the softening zone shown in Figure 2 correlates to the tempered sorbite region in Figure 1 (part f). The hardness maps shows that the fusion zone is approximately as hard as the base metal, with the supercritical HAZ having the highest hardness values before rapidly softening in the intercritical and subcritical HAZ zones. The softened region must be accounted for in designing CMT or other high heat input welded components.
Figure 1: a) Base metal with retained austenite between martensite lathes, b) fusion zone with acicular ferrite and ferrite, c) coarse martensite grains in supercritical HAZ, d) fine martensite grains and ferrite in supercritical HAZ, e) intercritical HAZ with fresh martensite and untransformed martensite, f) softest region in subcritical HAZ; shows tempered sorbite, g)zoomed in region of subcritical zone with precipitates, h) subcritical HAZ with 350-360HV hardness, i) hardness with 380-390HV.W-1
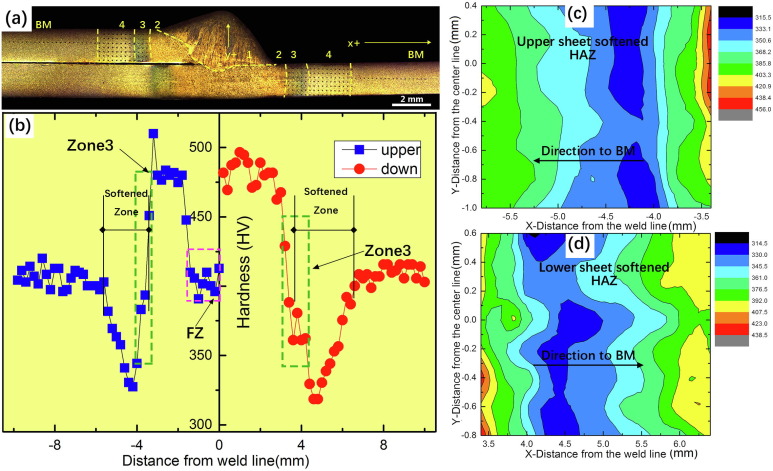
Figure 2: a) macrostructure of the CMT-welded QP1180 joint, b) hardness chart through joint, c) hardness map in upper sheet, d) hardness map in lower sheet. 1) fusion zone, 2) supercritical HAZ, 3) intercritical HAZ, 4) subcritical HAZ, BM = base metal.W-1
Arc Welding, Joining
A common issue when welding Advanced High-Strength Steels (AHSS) is with protective coatings causing weld defects. A group of researchers at the NMAM Institute of Technology and Dong-Eui University studied common issues with gas metal arc welding (GMAW) in the cold metal transfer (CMT) mode on a zinc-coated steel.V-2 The study used infrared thermography to observe the welds as they were created, helping to get detailed observations on some defects appearing in real time. With GMAW in CMT mode, the prevailing defect with welding a zinc-coated steel was porosity from metal vapors escaping through the weld. This issue could be addressed by adjusting the heat input and travel speed to provide more time for metal gases to escape.
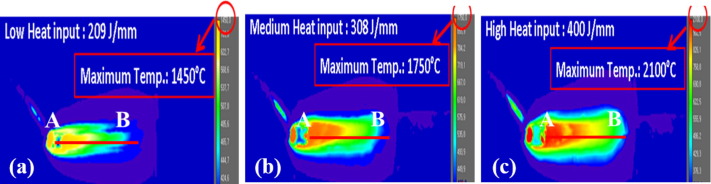
In Figure 1, it shows that with a higher heat input, more heat is in the weld puddle. In low and medium heat inputs, the puddle is above melting temperature, but not as high as the high heat input. Figure 2 shows that the low heat input also has the fastest solidification rate, and the high heat input has the slowest solidification rate. Figure 3 shows where the zinc vapors from the molten coating evaporate through the weld. In the left picture, at low heat input, the nucleation is contained inside of the weld, and the fusion zone would collect in the fusion zone. In the middle picture, at medium heat input, the zinc vapors bubble out just as the metal starts to solidify. In the right picture, at high heat input, the zinc bubbles out in the weld puddle while it is still molten.
Figure 1: Infrared Thermography of Weld Bead.V-2
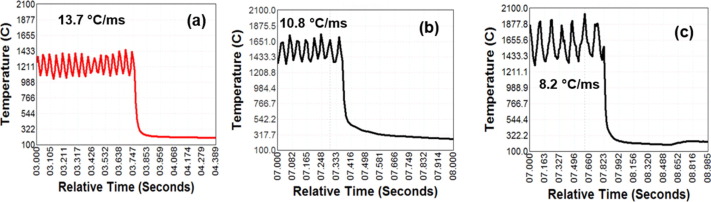
Figure 2: Variation of temperature during CMT for High, Medium, and Low Heat Input.V-2
Figure 3: Variation of Zinc Porosity Position vs Low, Medium, and High Heat Input.V-2
These factors combined indicate several factors that influence zinc porosity in GMAW CMT weldments. The researchers concluded that at low heat inputs, the zinc collects in the fusion zone. At medium heat inputs, the solidification rate and temperature gradient through the weld puddle traps the zinc in the fusion zone but also allows some to bubble out through the weld puddle. This caused the worst material properties of the three weldments for the researchers. At high heat inputs, the zinc bubbles out through the weld puddle, before solidification occurs. This condition is optimal, to reduce porosity with zinc metal vapors, the heat input should be increased so that the weldment temperature increases and solidification rate decreases.
