The article “Paint Bake Effect on Generation 3 Steel Weld Strength Compared to Other AHSS” by Richard H. Wolf explores the strength increase of resistance spot welds (RSW) in Generation 3 (Gen3) advanced high strength steels (AHSS) due to the paint bake-hardening effect.
These steels, due to their carbon content, may yield welds that can be brittle. A crucial, and often overlooked, aspect of the automotive production process is the paint bake stage, which has been shown to improve the mechanical properties of AHSS welds. In order to correctly assess the strength of a weld, this article proposes to take the paint-bake effect into account.

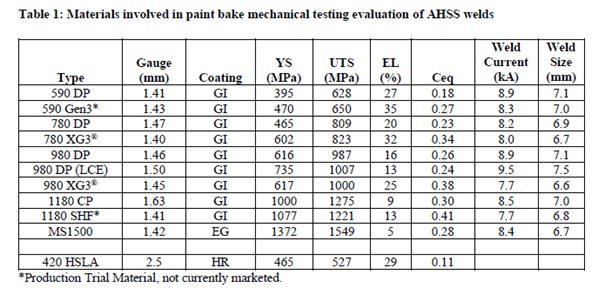
Table 1: Materials tested.
The experimental phase involved various AHSS materials, primarily with 1.5 mm thickness, with differing yield strengths and carbon equivalencies (Ceq). Resistance spot welding was performed under controlled conditions, and the effects of different paint bake temperatures and durations were analyzed.

Figure 1: Testing setup
Results indicated that Gen3 steels exhibited a significant increase in weld strength following paint baking, particularly in cross-tension strength (CTS) tests. Higher Ceq values correlated with lower weld strength in the as-welded state, while the paint bake effect tended to equalize these strengths across different alloys.
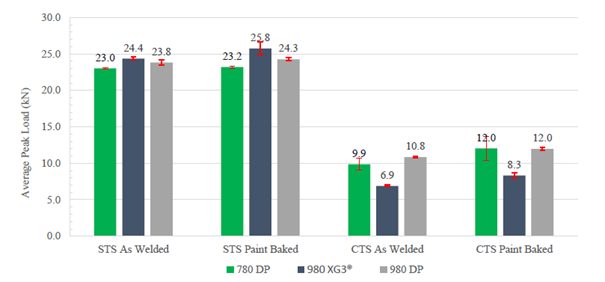
Figure 2: Comparison of shear-tensile strength and cross-tensile strength of different steels with and without paint baking. Especially in cross-tensile testing, a significant increase in load-bearing capacity is visible.
Hardness testing revealed a softening in the heat-affected zone after baking, suggesting that the weld microstructure became more homogenous, which reduces brittleness and improves fracture behavior. The investigation into heterogeneous welding between different steel types further elucidated the contribution of the fusion zone and heat-affected zone to overall weld strength.
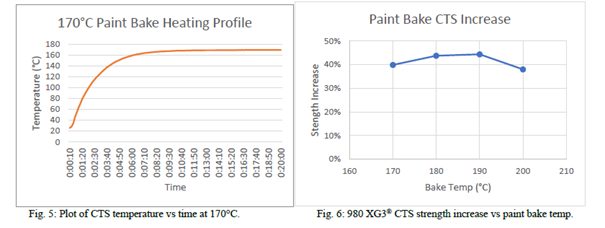
Figure 3: Utilized paint baking profile and cross-tensile strength increase
In conclusion, the paint bake process significantly enhances the strength of AHSS welds, especially for Gen3 steels. This improvement should be factored into weld strength modeling for automotive applications. The author suggests establishing standardized paint bake simulations to ensure weld properties are accurately represented for automotive manufacturers.
Source
Richard H. Wolf, Paint Bake Effect on Generation 3 Steel Weld Strength Compared to Other AHSS
Conventional HSS, Steel Grades
Carbon-Manganese High Strength Steel
Carbon and manganese are the two most cost-effective alloying additions to increase strength. While effective at strengthening, these additions reduce ductility and toughness, and make welding more challenging.
The practical usage of these grades typically limits the highest strength to no more than 280 MPa. Adding enough carbon and manganese to achieve higher strength results in a product without sufficient ductility for challenging applications, low toughness, and welding difficulty. These products sometimes are referred to as structural steels, and achieve their strength from the mechanism of solid solution strengthening.
Until the commercialization of High Strength Low Alloy steels, the CMn approach was the only option for users to obtain a high strength sheet metal.
Some of the specifications describing uncoated cold rolled Carbon-Manganese (CMn) or structural steels are included below, with the grades typically listed in order of increasing minimum yield strength and ductility. Different specifications may exist which describe hot or cold rolled, uncoated or coated, or steels of different strengths. Many automakers have proprietary specifications which encompass their requirements. Note that ASTM terminology is based on minimum yield strength, while JIS and JFS standards are based on minimum tensile strength. Also note that JIS G3135 does not explicitly state that these grades must be supplied with a C-Mn chemistry. An HSLA approach is satisfactory as long as the mechanical property criteria are satisfied.
- ASTM A1008M, with the terms Grade 25 [170], Grade 30 [205], Grade 33 [230] Type 1, Grade 33 [230] Type 2, Grade 40 [275] Type 1, Grade 40 [275] Type 2, Grade 45 [310], Grade 50 [340], Grade 60 [410], Grade 70 [480], and Grade 80 [550] A-25
- JIS G3135 with the terms SPFC340, SPFC370, SPFC390, SPFC440, SPFC490, SPFC540, and SPFC590 J-3
- JFS A2001, with the terms JSC340W, JSC370W, JSC390W, and JSC440W J-23
Conventional HSS, Steel Grades
Carbon-Manganese Steels (CMn) are a lower cost approach to reach up to approximately 280MPa yield strength, but are limited in ductility, toughness and welding.
Increasing carbon and manganese, along with alloying with other elements like chromium and silicon, will increase strength, but have the same challenges as CMn steels with higher cost. An example is AISI/SAE 4130, a chromium-molybdenum (chromoly) medium carbon alloy steel. A wide range of properties are available, depending on the heat treatment of formed components. Welding conditions must be carefully controlled.
The 1980s saw the commercialization of high-strength low-alloy (HSLA) steels. In contrast with alloy steels, HSLA steels achieved higher strength with a much lower alloy content. Lower carbon content and lower alloying content leads to increased ductility, toughness, and weldability compared with grades achieving their strength from only solid solution strengthening like CMn steels or from alloying like AISI/SAE 4130. Lower alloying and elimination of post-forming heat treatment makes HSLA steels an economical approach for many applications.
This steelmaking approach allows for the production of sheet steels with yield strength levels now approaching 800 MPa. HSLA steels increase strength primarily by micro-alloying elements contributing to fine carbide precipitation, substitutional and interstitial strengthening, and grain-size refinement. HSLA steels are found in many body-in-white and underbody structural applications where strength is needed for increased in-service loads.
These steels may be referred to as microalloyed steels, since the carbide precipitation and grain-size refinement is achieved with only 0.05% to 0.10% of titanium, vanadium, and niobium, added alone or in combination with each other.
HSLA steels have a microstructure that is mostly precipitation-strengthened ferrite, with the amount of other constituents like pearlite and bainite being a function of the targeted strength level. More information about microstructural components is available here.
Some of the specifications describing uncoated cold rolled high strength low alloy (HSLA) steel are included below, with the grades typically listed in order of increasing minimum yield strength and ductility. Different specifications may exist which describe hot or cold rolled, uncoated or coated, or steels of different strengths. Many automakers have proprietary specifications which encompass their requirements. Note that ASTM, EN and VDA terminology is based on minimum yield strength, while JIS and JFS standards are based on minimum tensile strength. Also note that JIS G3135 does not explicitly state that these grades must be supplied with an HSLA chemistry. A C-Mn approach is satisfactory as long as the mechanical property criteria are satisfied.
- ASTM A1008M, with the terms HSLAS 45[310], 50[340], 55[380], 60[410], 65[450], and 70[480] along with HSLAS-F 50 [340], 60 [410], Grade 70 [480] and 80 [550]A-25
- EN10268, with the terms HC260LA, HC300LA, HC340LA, HC380LA, HC420LA, HC460LA, and HC500LAD-5
- JIS G3135, with the terms SPFC340, SPFC370, SPFC390, SPFC440, SPFC490, SPFC540, and SPFC590J-3
- JFS A2001, with the terms JSC440R and JSC590RJ-23
- VDA239-100, with the terms CR210LA, CR240LA, CR270LA, CR300LA, CR340LA, CR380LA, CR420LA, and CR460LAV-3
![Yield Strength]()
Mechanical Properties
Forming forces need to exceed the yield strength for plastic deformation to occur and an engineered stamping to be produced. If a metal structure is loaded to a level below the yield strength, only elastic deformation occurs, and the load can be removed. With no permanent (plastic) deformation, the metal returns to its original shape.
On the stress-strain curve, yielding occurs where the initial linear region transitions to the non-linear portion. This transition does not occur always at a clearly visible well-defined point. Consistent yield strength measurement is facilitated by defining how this parameter should be determined. Two techniques are used when working with sheet metals. The most common method is to draw a line parallel to the modulus line at an offset strain of 0.2%. The intersection stress becomes what is defined at the “0.2% offset yield strength” (Figure 1). This value is referred to as Rp0.2. The second technique is drawing a vertical line at the 0.5% strain value until it crosses the stress-strain curve. This determines the “yield strength at 0.5% extension under load,” abbreviated as Rt0.5 (Figure 2). These techniques result in similar – but not identical – values for yield strength.

Figure 1: 0.2% offset yield strength, determined by offset of a line parallel to the modulus line by 0.2% strain.

Figure 2: Yield strength at 0.5% extension under load, determined by a vertical line offset from the origin by 0.5% strain
Some metals have yield point elongation (YPE) or Lüders bands. Deforming metal is locked in place by interstitial carbon and nitrogen atoms and other restrictive features of the microstructure. Load increases with little corresponding deformation – or put another way, stress increases with only an incremental increase in strain. The highest stress reached is known as the upper yield strength or upper yield point. Once a band of deformed (yielded) metal breaks free from being pinned by dislocations in the microstructure, the stress drops and there is an increase in strain. The lowest stress reached is known as the lower yield strength or lower yield point (Figure 3). The bands of deforming metal are known as Lüders bands, named after one of the people first observing the phenomenon. Lüders deformation continues at approximately a constant stress until the entire sample has yielded, and the sample begins to work harden. The total strain associated with this type of deformation is known as yield point elongation, or YPE. Stabilized, interstitial-free, vacuum degassed steel, such as ULC EDDS are not at risk of aging, and will not exhibit YPE. For those grades susceptible to YPE, leveling prior to sheet forming will minimize this tendency.

Figure 3: Defining upper yield stress, lower yield stress, and yield point elongation.
Since springback is proportional to the yield strength of the steel, knowing the yield strength allows some estimation of relative springback. Figure 4 compares mild steel, HSLA 700Y/800T, and MS 1500 AHSS having a 1400MPa yield strength. The relative magnitude of springback is indicated by the arrows shown on the horizontal axis, and reflects the increase of springback with yield strength.
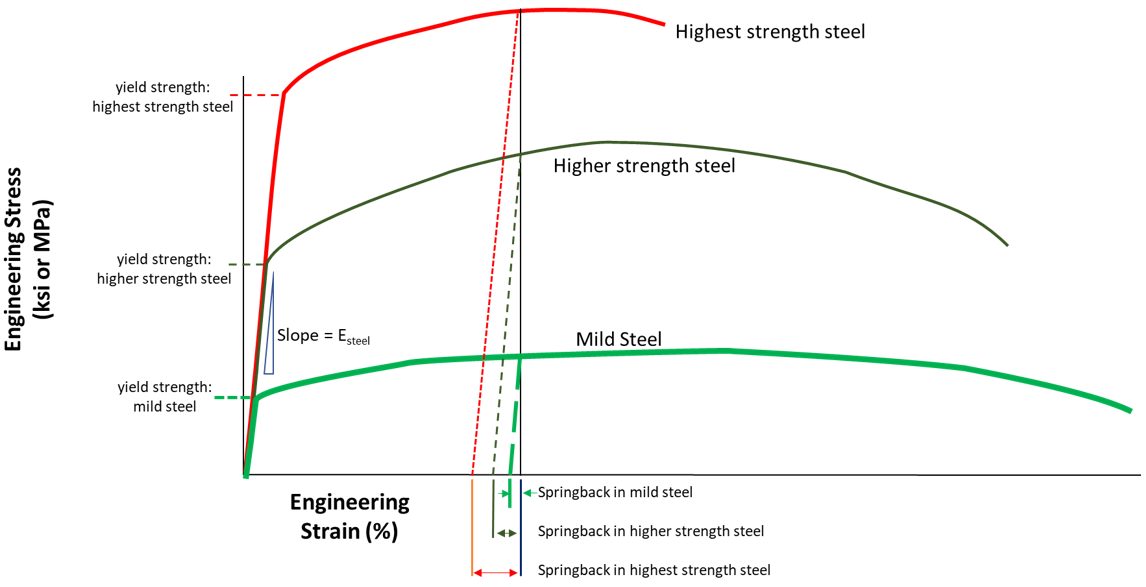
Figure 4: Springback is proportional to yield strength.
![Yield Strength]()
Testing and Characterization
topofpage
Tensile testing characterizes the forming and structural behavior of sheet metals. The test involves loading a sample with a well-defined shape along the axis in tension, generally to fracture, and recording the resultant load and displacement to calculate several mechanical properties. Global standardsI-7, A-24, D-19, J-15 prescribe the conditions under which tests must occur.
Sample Size and Shape
Full-size samples for tensile testing of metal sheets have a rectangular section at the edges for gripping by the test machine. Reducing the width in the central area promotes fracture in the monitored region. These geometrical features result in a sample shape which resembles a dogbone, leading to a descriptive term applied to test samples.
Dimensions of the dogbone samples are associated with tensile test standard from which they apply. ISO I, II, and III (described in Citation I-7) corresponds to the ASTMA-24, DIND-19, and JISJ-15 shapes, respectively. Figure 1 shows the dogbone shapes, highlighting the critical dimensions of width and gauge length. Refer to the Test Standards for other dimensions, tolerances, and other requirements.

Figure 1: Full-size tensile sample shapes for ISO I (ASTM), ISO II (DIN), and ISO III (JIS) standards.I-7, A-24, D-19, J-15
Significant differences exist in the width and gauge length of these tensile bar shapes. Although the ASTM and JIS bars have similar gauge length, the width of the JIS bar is twice that the ASTM bar. The ASTM and DIN bars have a 4:1 ratio of gauge length to width, where the JIS bar has a 2:1 ratio.
These shape differences mean that the calculated elongation changes depending on the test-sample standard used, even when testing identical material. With the combination of the shortest gauge length and widest sample, elongation from JIS bars typically are higher than what would be generated from the other shapes.
Yield strength and tensile strength are not a function of the shape of the tensile bar. Strength is defined as the load divided by the cross-sectional area. Even though each of the bars specify a different sample width (and therefore different cross-section), the load is normalized by this value, which negates differences from sample shape.
Shearing or punching during sample preparation may work-harden the edges of the tensile bar, which may lead to generating an inaccurate representation of the mechanical properties of the sheet metal. Test Standards require subsequent machining or other methods to remove edge damage created during sample preparation. Milling or grinding the dogbone samples minimizes the effects sample preparation may have on the results.
Tensile Test Procedure
The gauge length is the reference length used in the elongation calculations. Depending on the test standard, the gauge length is either 2 inches, 80 mm, or 50 mm. Multiplying the width and thickness within the gauge length determines the initial cross-sectional area before testing.
Grips tightly clamp the edges of the sample at opposite ends. As the test progresses, the grips move away from each other at a prescribed rate or in response to the restraining load. A load cell within the grips or load frame monitors force. An extensometer tracks displacement within the gauge length. Samples are typically tested until fracture.
During the tensile test, the sample width and thickness shrink as the length of the test sample increases. However, these dimensional changes are not considered in determining the engineering stress, which is determined by dividing the load at any time during the test by the starting cross-sectional area. Engineering strain is the increase in length within the gauge length relative to the starting gauge length. (Incorporating the dimensional changes occurring during testing requires calculating true stress and strain. The differences between engineering and true stress/strain are covered elsewhere (hyperlink to 2.3.2.1-Engineering/True)
A graph showing stress on the vertical axis and strain on the horizontal axis is the familiar engineering stress-strain curve, Figure 2. From the stress-strain curve, numerous parameters important for sheet metal forming appear, including:

Figure 2: Engineering stress-strain curve from which mechanical properties are derived.
Influence of Test Speed
Conventional tensile testing is done at strain rates slow enough to be called “quasi-static.” These rates are several orders of magnitude slower than the deformation rates during stamping, which itself is several orders of magnitude slower than what is experienced during a crash event.
Stress-strain curves change with test speed, typically getting stronger as the speed increases. The magnitude of these changes varies with grade. Significant challenges exist when attempting to characterize the tensile response at higher strain rates. Improved equipment and data collection capabilities are among the required upgrades.
Influence of Tensile Test Equipment
Advanced High-Strength Steels (AHSS) may challenge older test equipment. The load and displacement response must reflect only the contributions of the sheet metal, and not be influenced by the load frame and other testing equipment. In much the same way that insufficiently stiff press crowns deflect when stamping AHSS parts, tensile test load frames may similarly deflect, resulting in inaccuracies in the load-displacement measurements.
Grip strength also becomes critical when testing AHSS samples. The high strength of the metal sheets requires more grip pressure to prevent sample slippage through the grips. Pneumatic grips and even some mechanical grips may not generate the necessary pressure. Hydraulically actuated grips may be necessary as the strength increases.
Back to the Top





