Forming Archives - Page 8 of 12

Fatigue

Normal vehicle use leads to repeated loading of components and joints. Stress concentrations in the body structure may lead to plastic strains at stresses below the yield strength due to cyclic fatigue. Conventional High-Strength Steel fatigue behavior correlates with their tensile strength. However, in multiphase steels, the strain distribution between phases within the steel microstructure affects the fatigue response, leading to a different response depending on which phases accommodate the strain.

The fatigue strength of DP steels is higher than that of precipitation-hardened steels or fully bainitic steels of similar yield strength for several metallurgical reasons. The dispersed fine martensite particles retard the propagation of fatigue cracks. For TRIP steels, the transformation of retained austenite can relax the stress field and introduce a compressive stress that can also improve fatigue strength. General categorization may not be possible – studies have reported cyclic hardening occurs in Dual Phase steels where the martensite volume fraction is less than 0.5 while Dual Phase steels at higher martensite content (higher strength) soften under cyclic loading conditions. ^C-15, ^W-27 Furthermore, fatigue limits are complicated by environmental factors like the presence of hydrogen.

Figures 1 and 2 illustrate the general improvements in fatigue capability offered by Advanced High-Strength Steel (AHSS) grades.

Figure 1: Fatigue characteristics of TRIP steel CR450Y780T-TR compared to conventional steels.^T-24

Figure 2: Fatigue limit for AHSS compared to conventional steels.^T-2

The table below lists some fatigue properties for conventional and advanced high strength steels.

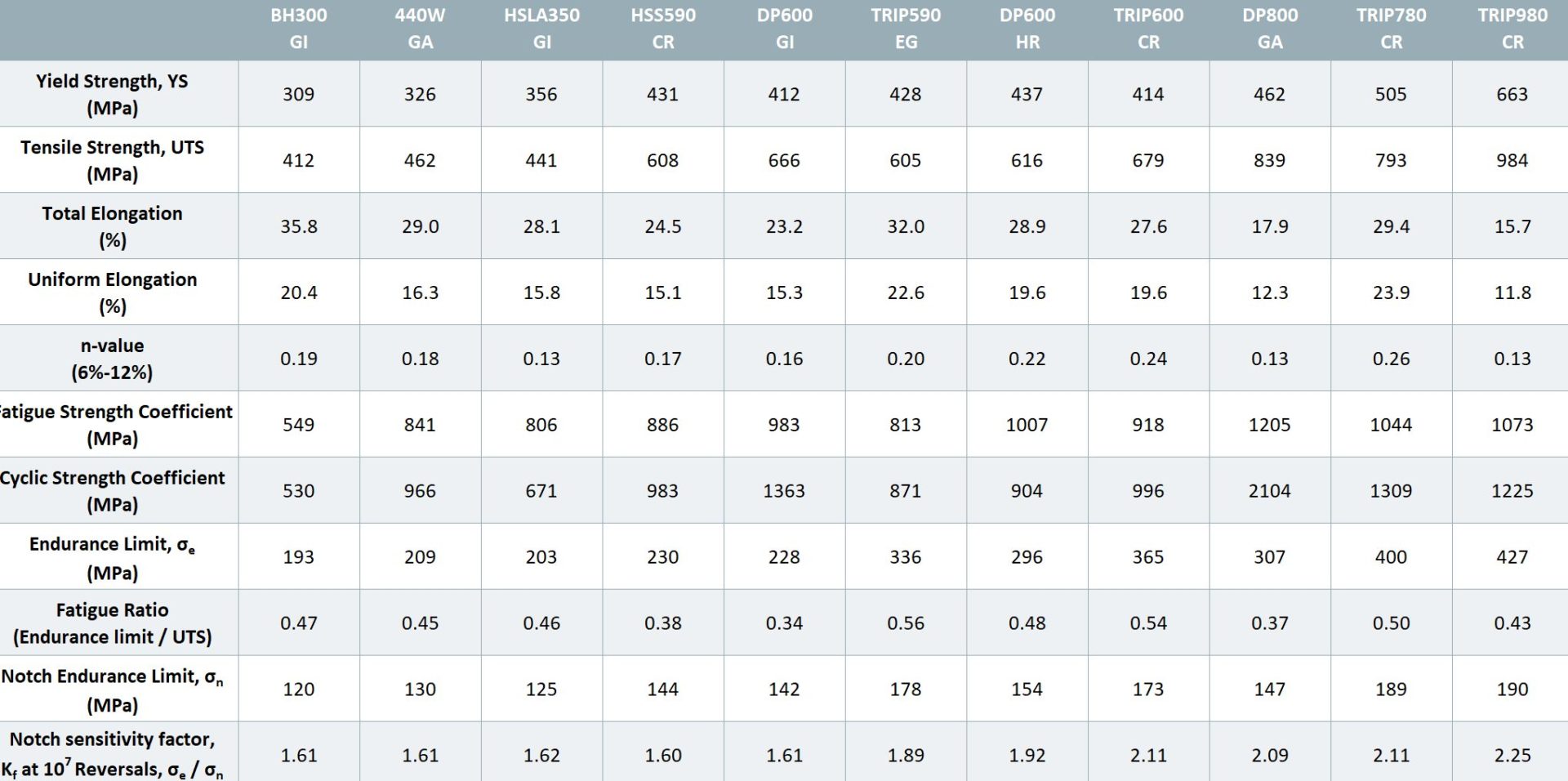
Table caption: Fatigue properties for HSS and AHSS grades Y-11

Table 1: Fatigue properties for HSS and AHSS grades ^Y-11

Shear Affected Zone

Cutting, Cutting-Blanking-Shearing-Trimming

A cut edge has four distinct zones with different characteristics:

Rollover – The plastically deformed zone bent as the cutting tools contact the edge of the sheet surface.
Burnish – The zone where the cutting tools penetrate into the sheet metal, prior to any fracturing. The sheet metal stresses are such that the surface compresses into the cutting tool, which gives it a flat, smooth, and shiny appearance. The shear zone is another name for this region.
Fracture – The zone where the cutting steels fracture the sheet metal, leading to separation from the remainder of the sheet. The surface of this region is rougher than the burnish zone, and is at an angle from the cutting direction.
Burr – The metal elongated and pushed out on the trailing edge of the cut.

The cutting process also deforms the metal near the shear face, creating what is known as the shear affected zone (SAZ). The degree and influence of this deformation is a function of the cutting process (shearing, water jet, laser, and so on) as well as the steel microstructure and strength. Many studies conclude plastic deformation within the SAZ is a key contributor to sheared edge stretching failures.

The Shear Affected Zone is the area of work-hardened steel and microstructural damage behind the sheared edge. The deformation pattern in the SAZ includes a large shear-induced rotation of the grains that increases with proximity to the sheared edge. An etched cross-section such as that shown in Figure 1 highlights the grain rotation and gives a visual indication of the size of the zone.

Figure 1: Shear Face Components and Shear Affected Zone.^K-1

Work hardening in the SAZ leads to a way to quantify the depth of the SAZ: by creating a hardness profile with readings starting at the edge and progressing deeper into the metal. The end of the SAZ occurs when the hardness readings level off to the bulk hardness.

Figure 2 compares the edge and hardness readings for CP800 and DP780, showing the depth of the SAZ for DP780 is about 41% of the initial sheet thickness of 1.56 mm, and the depth of the CP800 SAZ is 20% of the initial 2.90 mm sheet thickness.^P-12

Figure 2: A) Sheared edge and SAZ of CP800; B) Sheared edge and SAZ of DP780; C) CP800 microstructure away from edge; D) DP780 microstructure away from sheared edge; E) hardness profile for the two sheared edges in the rolling direction.^P-12

Plastic deformation from cutting and subsequent edge expansion forms micro-voids and creates other microstructural damage. The voids grow and combine with neighboring voids to create micro-cracks, which in turn combine with other micro-cracks resulting in the cracks that cause fractures in stampings.

Void nucleation in DP steels occurs through two mechanisms: decohesion of the ferrite-martensite interface or fracture of martensite islands.^P-12^{, A-27,} ^A-28 Figure 3 shows an example of both.

Figure 3: Aligned voids along loading direction. White solid square shows interface damage between martensite and ferrite. White dashed circles show voids formed by cracking of martensite.^A-28

The study in Citation P-12 compared CP800 and DP780. The CP800 microstructure contains ferrite, bainite, and martensite. The DP780 microstructure has more martensite, with a larger strength differential between the phases, which combines to result in a lower nucleation strain and accelerated void nucleation compared with CP800. The DP grade has a larger SAZ, further promoting nucleation, growth, and coalescence of voids. This results in failure at a lower strain and leads to the lower edge stretchability of the DP780 compared to the CP800 alloy.^P-12 The ductility of bainite restrains void initiation at high strains, which may play a role in improved sheared edge performance.^{S-24, S-25}

Fracture initiation energy, a measure of fracture toughness correlates with hole expansion and stretch-ﬂangeability as shown in Figure 4.^Y-5

$Figure 4: Correlation between fracture initiation energy and hole expansion ratio of various metals. Steels A – D are AHSS grades with Tensile strength ranging from 725 – 1000 MPa.Y-5$

Figure 4: Correlation between fracture initiation energy and hole expansion ratio of various metals. Steels A – D are AHSS grades with Tensile strength ranging from 725 – 1000 MPa.^Y-5

In addition to microstructural damage and fracture mechanics, simulation models improve in accuracy when the incorporating the effect of the temperature increase in the localized deformation zone. Simulation of the blanking of AISI 1050 shows a temperature at the cut edge of 440 °C. The edge temperature may be even higher in AHSS grades due to their higher strength.^A-29

Figure 5: 1.27mm AISI 1050 steel blanked with 15% clearance. The simulation shows temperature, with the cut face getting as hot as 440 °C.^A-29

When factoring in the considerations described here, simulation accuracy of hole expansion and sheared edge stretching improves significantly. Citations L-13 and L-14 provide additional background information about the Shear Affected Zone.

Non-Linear Strain Paths (Stress-Based FLCs)

FLC and FLD

Conventional Forming Limit Curves (FLCs) gained widespread industrial use since being introduced by Dr. Stuart Keeler in the 1960’s. Applications from feasibility analysis to stamping plant troubleshooting use these principles. The strain hardening exponent (n-value) and thickness are inputs into a shortcut to create the curve placement and shape, but this is applicable to only mild steels, conventional High-Strength Steels, and some Advanced High-Strength Steels. Furthermore, this shortcut is an approximation, coming from a best-fit curve generated from data points gathered over multiple grades.

A typical method used in creating most FLCs includes deforming samples of different widths with a 100 mm (4 inch) diameter hemispherical punch – known as the Nakajima method. An alternate approach uses a flat-bottom cylindrical punch, known as the Marciniak method (Figure 1). Independent of the punch shape used, generating FLCs involves measuring the strains resulting from deforming a blank to a formed shape. The conventional FLC plots major strain on the vertical axis against minor strain on the horizontal axis. This FLC applies only to in-plane stretching in linear strain paths, and assumes that there are no through-thickness stress or strain differences. Assessing bendability or cut edge ductility is not possible with this approach.

Figure 1: Punch Shape Used to Create Forming Limit Curves Result in Through-Thickness Strain Differences Which Influence the Shape and Placement of The FLC [Reference 1]

Figure 1: Punch Shape Used to Create FLCs Result in Through-Thickness Strain Differences Which Influence the Shape and Placement of The FLC ^S-37

Figure 2 compares the FLCs generated by deforming DP980 with the three punch shapes highlighted in Figure 1. Note the higher strains associated with the 50 mm diameter hemispherical punch compared with the strains generated from the 100 mm diameter hemispherical punch. This punch curvature difference impacts the magnitude of the strains that develop through the thickness of the sheet. On samples deformed with a hemispherical punch, the selected strain measurement technique (circle/square grid analysis or Digital Image Correlation, for example) directly measures strains on the outer top surface only, with the middle and inner surface having progressively lower strains as a function of the R/T ratio. A punch or feature with small R/T leads to high strains on the outermost surface. Strains exceeding the FLC on only this outer surface will not lead to necks on the formed panel. Exceeding the FLC through the entire thickness – from the inner surface to the outer surface – must occur for the sample to show a neck.^T-17

Figure 2: FLCs of the same batch of DP980 Showing Dependence on Punch Shape and Curvature [References 1 and 3]

Figure 2: FLCs of the same batch of DP980 Showing Dependence on Punch Shape and Curvature.^S-37, ^M-15

In addition to the through-thickness strain differences from the punch curvature, the metal flow differences resulting from the punch shapes leads to directional changes in the strain path taken by the deforming metal. A channel drawn part with a hat-shaped cross section in which there are no features like embossments is likely to have a linear strain path. Forming every other engineered stamped part geometry involves some degree of a non-linear strain path (NLSP).

The importance of strain path and deformation history comes from the changes in the forming limit that occur once metal deformation starts. The black curve in Figure 3 shows the FLC for an alloy generated in a conventional manner with as-received metal, assuming a linear strain path. The red curve results from testing the same metal that initially stretched to an equal-biaxial plastic pre-strain of 0.07. In this strain path, substantially less deformation can occur before reaching the forming limit. However, the strain path changes if the local part contour is different, and that strain path results in a different amount of subsequent deformation prior to necking. The magnitude and direction of the shift changes based on the strain and the orientation relative to the rolling direction. Citation S-38 highlights these curves and presents more examples of the effects of different strain paths. The important conclusion is that the amount of deformation that a metal is capable of withstanding prior to necking changes throughout the forming process and depends on the local part shape (among other variables), and cannot be discerned by using only the conventional strain based FLC.

Figure 3: Experimental FLCs for a linear strain path (in black) and for a bilinear strain path after 0.07 strain in equal biaxial tension in strain space (in red) ^S-38

Figure 4 shows the strain paths associated with the FLCs presented in Figure 2, with along with a magnified portion of one of the curves. This non-linearity is a characteristic of samples formed with a dome, associated with the sample wrapping around the punch during the initial contact and experiencing a combination of biaxial bending and stretching. Citation M-15 presents a method to correct for strain path effects.

Figure 4: Strain Path for FLCs shown in Figure 2. A) 100 mm diameter flat punch; B) 100 mm diameter hemispherical punch; C) 50 mm diameter hemispherical punch; and D) Magnified portion of one curve from Figure 4B showing the non-linearity of the strain path.^S-37, ^M-15

Accounting for tool contact pressure is critical as well, since pressure through the sheet thickness suppresses the onset of necking. Applying this compensated FLC in simulation or in hands-on analysis parts analysis requires modification for the unique characteristics of each part, with appropriate adjustments for local curvature, contact pressure and deformation history. Citations S-37 and M-15 detail methods to compensate for the effects of strain path, curvature, and tool pressure. Figure 5 shows that after incorporating these corrections, the curves condense to one shape independent of the variables used.

Figure 5: As-generated FLCs compared with FLCs after strain path, curvature, and tool contact pressure corrections [References 1 and 3]

Figure 5: As-generated FLCs compared with FLCs after strain path, curvature, and tool contact pressure corrections.^S-37, ^M-15

In summary, FLCs generated from relatively similar simple tools are sensitive to small differences in R/T ratio, incorporation of tool contact pressure, and deviations from a linear strain path. By comparison, engineered stampings require substantially more complex tool shapes with differing degrees of curvature, tool contact pressure, and strain paths all within one part. These complex part shapes contribute to an even wider variation in the yield surface and hardening mechanisms important for simulation, and impacts predictions of formability, springback, and stress analysis.

A common requirement during tooling buyoff – where all strains need to be below the FLC by at least a certain amount called the safety margin – magnifies these challenges. AHSS grades already have low FLCs relative to their lower strength counterparts, so it is critical that the chosen FLC does not further reduce efficient application of these grades. Minimizing sensitivity to the changes in strain path occurring across a complex part requires using a different approach – a FLC with the axes in stress-space rather than the conventional strain-space.

This discussion has centered on conventional strain-based FLCs, which incorporate an assumption of a linear strain path as a flat sheet deforms to the final shape. Stress-based Forming Limit Curves (sFLC or FLSC) are insensitive to deformation history and can be adjusted to reflect the differences in local tool geometry or contact pressure across the stamping. Forming analysis software readily converts conventional FLCs into stress-based units. Figure 6 converts the two strain paths presented in Figure 3 into stress-space, and shows the two experimental stress FLCs generated with different strain paths are independent of the loading history and essentially overlap. Citations S-38, S-39, S-40 and S-41 contain information about stress-based FLCs, as well as their generation and usage.

Figure 6: After converting the conventional FLCs in Figure 3 to stress-space, the experimental stress-based FLCs show no significant differences.^S-38

Citation H-20 presents a related method to transition from strain-based to stress-based Forming Limit Curves. The proposed stress-based failure criterion postulates that localized necking occurs when a critical normal stress condition is met. This approach adequately describe the experimental strain-based forming limit data in most evaluated materials, failing only with a 3rd Generation AHSS alloy containing a high percentage of retained austenite. For this grade, the authors speculate that a material model more advanced than the one employed in this study will improve correlation.

Accurate simulation requires accurate and complete inputs, including the full range of metal properties, with correct material flow and hardening models, and an understanding of the conditions that will produce failure. Any shortcuts taken increases the likelihood that simulation will not fully match reality for all materials, part shapes, and production processes. A conventional strain-based FLC assumes no effect of part geometry, tool contact pressure, and deformation history – all of which occur on engineered stampings to differing degrees. Analysts should incorporate stress-based FLCs into their simulation with appropriate adjustments to address local geometry and contact pressure to ensure an accurate representation of the metal’s forming characteristics.

For use in the die shop or stamping plant, a growing number of optical systems have built-in features to map strain measurements on to an sFLC. Use caution when employing this approach since these systems measure only the final net strain, and not the strain history as the panel deforms. Proper application involves capturing metal flow from individual breakdown panels and adjusting the FLC accordingly as the panel gets closer to the home position.

Special thanks to Dr. Thomas Stoughton, Technical Fellow, General Motors Research & Development, for assistance in preparing this information.

Drawing

Forming Modes

Drawing is the sheet metal forming process where the punch that creates the part shape forces the sheet metal to pull in from the flange area. In contrast with stretch-drawing or stretch forming, little metal thinning occurs in pure drawing. There is not a generally accepted definition for the term “deep drawing,” although some references describe it as when the depth of draw is greater than the diameter.

Drawability, or the ability for a sheet metal to be drawn into a cup, is assessed by the cup drawing test to measure the Limiting Draw Ratio, or LDR. Here, a cylindrical punch contacts and then pushes a circular blank into the die (Figure 1). The ratio of the largest blank diameter successfully drawn into a cup to the punch diameter used for drawing is the LDR.

Figure 1: In the cup drawing test, a punch deforms a circular blank into a cylindrical cup. The largest ratio of blank diameter to punch diameter successfully drawn into a cup is the Limiting Draw Ratio (LDR).

In the LDR test, metal in the circular blank flows over the die radius and into the cup wall. The metal movement from the flat blank to the vertical sidewalls is the only metal movement which happens, since there is no metal flow within the flat bottom region.

As shown in Figure 2, the flange of the circular blank undergoes radial tension and a circumferential compression as the flange moves in a radial direction towards the circular die radius in response to a pull generated by a flat bottom punch. Blank holder pressure is set to prevent buckles in the blank.

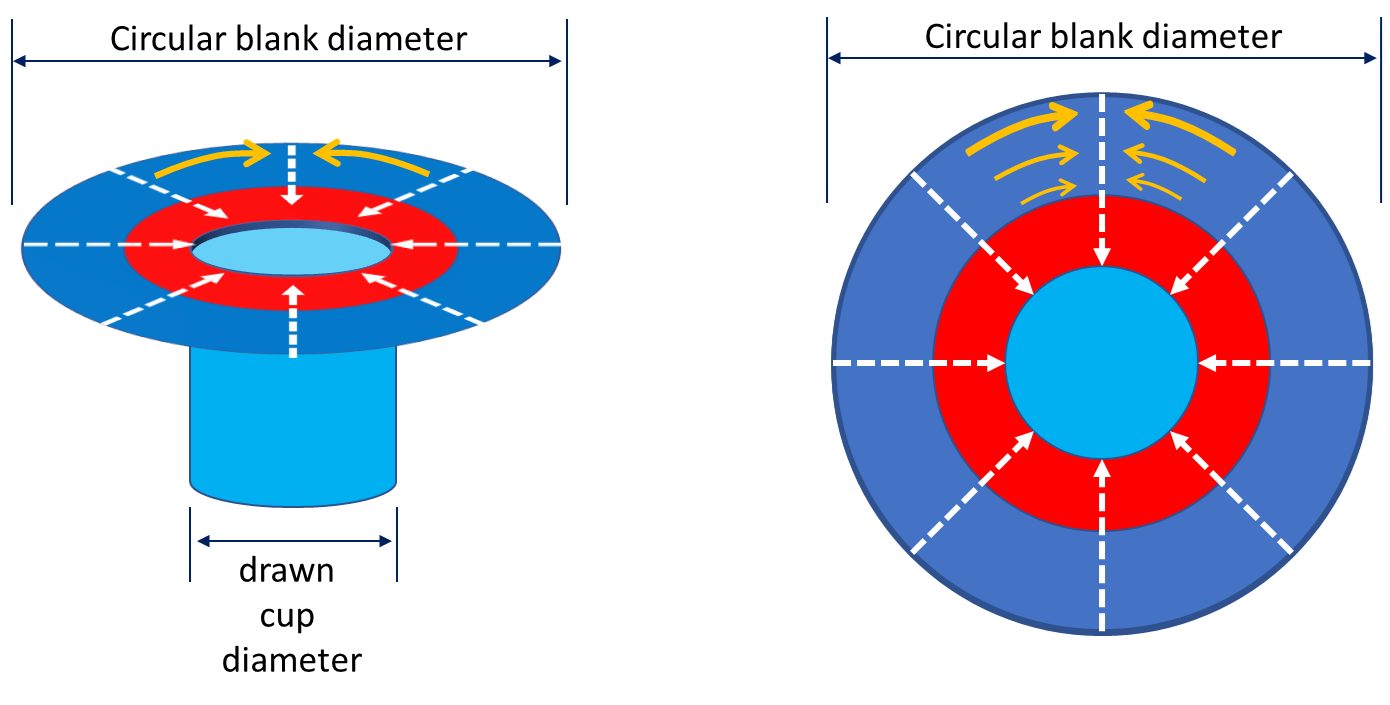
Figure 2: Tension and compression in a drawn cup. Dashed white arrows indicate the radial tension created during cup forming; orange arrows indicate flange compression as a greater amount of metal feeds into progressively smaller regions.

The steel property that improves cup drawing or radial drawing is the normal anisotropy or r_m value. Values greater than 1 increase in the Limiting Draw Ratio. In contrast, the LDR is insensitive to the strength of the steel and the n-value. High-strength steels with UTS greater than 450 MPa and hot-rolled steels have r_m values approximating one and LDR values between 2.0 – 2.2. Therefore, DP and HSLA steels have similar LDR values. However, TRIP steels have a slightly improved LDR deep drawability.^T-2 Since the transformation of retained austenite to martensite is influenced by the deformation mode (Figure 3), the amount of transformed austenite to martensite generated by shrink flanging in the flange area is less than the plane strain deformation in the cup wall. This difference in transformation from retained austenite to martensite makes the wall area stronger than the flange area, thereby increasing the LDR. The benefit of the increased LDR is seen in Figure 4 which shows cups formed from different grades having the same tensile strength.

Figure 3: The cup wall in plane strain strengthens more than the shrink flange due to increased amounts of transformed martensite in TRIP steels.^T-2

Figure 4: Cups formed from 590MPa tensile strength steels, highlighting greater draw depths possible with TRIP steels.^T-2

In a study of different grades^C-9, laboratory cup drawing experiments show an approximate LDR of 2.0 – 2.2 for the DP steels tested (Figure 5). Note that a doubling of the yield strength has no effect on the LDR. An increased r_m value of mild steel created a small increase in LDR over DP steel. The LDR of the MS (martensitic) steel evaluated may have been impacted by the reduced bendability going over the die radius. Figure 6 shows the cup draw depths possible for the grades reported in Figure 5.^S-26

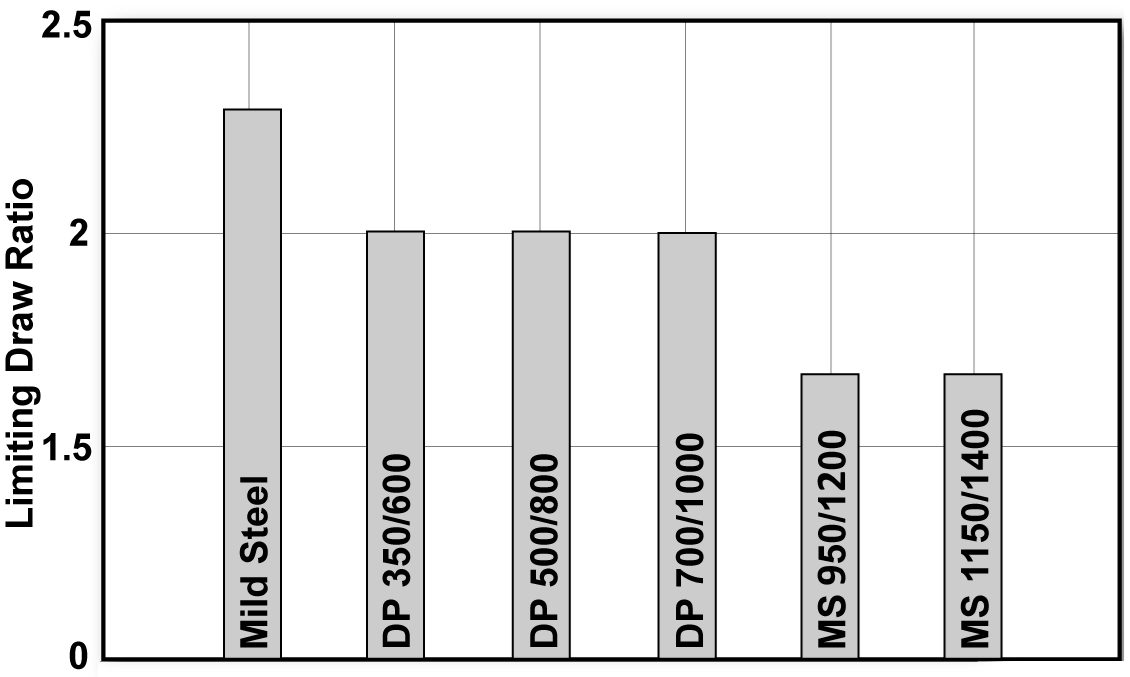
Figure 5: LDR tests for Mild, DP, and MS steels.^C-9

Figure 6: Cups used in the testing reported in Figure 5.^S-26

Even though r-value is the only steel property influencing the formability of drawn flat-bottom cups through its relationship with LDR, not all cups have flat bottoms. Some have hemispherical or other configurations for bottoms. Adding a dome-like shape to the cup results in a more complex forming operation which is now sensitive to material properties like n-value and microstructures.

Corners of box-shaped stampings and the ends of closed channels contain design features similar to drawn cups, providing insight on an analytical approach.

The four corners of a box-shaped drawn panel should each be analyzed as one-quarter of a cup. Buckles forming in the binder area indicate compressive flow. The corners of the blank will form the same as a deep drawn cup.
The side walls are formed by metal flowing from the binder across the die radius. The term for this metal flow is bend-and-straighten.

In summary, higher LDR values are achievable in steels with greater values of the normal anisotropy ratio, r_m. The absolute value of the LDR, however, also depends on the lubrication, blank holder load, die radius and other system inputs. Figure 7 compares a higher viscosity lubricant on the left with a lower viscosity lubricant on the right.^S-26 Die radii need to be balanced: large radii promotes metal flow and may lead to wrinkles, while small radii restricts metal flow and may lead to splits.

Figure 7: The influence of lubricant viscosity on drawing. The cup formed with the higher viscosity lubricant is on the left.^S-26

Engineering Stress-Strain vs. True Stress-Strain

Formability

Strength is defined as load divided by cross-sectional area. In a tensile test, the choice of when the cross-sectional area is measured influences the results.

It is easiest to measure the width and thickness of the test sample before starting the pull. At any load, the engineering stress is the load divided by this initial cross-sectional area. Engineering stress reaches a maximum at the Tensile Strength, which occurs at an engineering strain equal to Uniform Elongation. After that point, engineering stress decreases with increasing strain, progressing until the sample fractures.

However, metals get stronger with deformation through a process known as strain hardening or work hardening. As a tensile test progresses, additional load must be applied to achieve further deformation, even after the “ultimate” tensile strength is reached. Understanding true stress and true strain helps to address the need for additional load after the peak strength is reached.

During the tensile test, the width and thickness shrink as the length of the test sample increases. Although these dimensional changes are not considered in determining the engineering stress, they are of primary importance when determining true stress. At any load, the true stress is the load divided by the cross-sectional area at that instant.

The true stress – true strain curve gives an accurate view of the stress-strain relationship, one where the stress is not dropping after exceeding the tensile strength stress level.

True stress is determined by dividing the tensile load by the instantaneous area.
True strain is the natural logarithm of the ratio of the instantaneous gauge length to the original gauge length.

True stress – true strain curves of low carbon steel can be approximated by the Holloman relationship:

σ = Kεⁿ

where true stress = σ; true strain = ε, n is the n-value (work hardening exponent or strain hardening exponent), and the K-value is the true stress at a true strain value of 1.0 (called the Strength Coefficient).

True stress-strain curves obtained from tensile bars are valid only through uniform elongation due to the effects of necking and the associated strain state on the calculations. Inaccuracies are introduced if the true stress-true strain curve is extrapolated beyond uniform strain, and as such a different test is needed. Biaxial bulge testing has been used to determine stress-strain curves beyond uniform elongation. Optical measuring systems based on the principles of Digital Image Correlation (DIC) are used to measure strains. The method by which this test is performed is covered in ISO 16808.^I-12

Stress-strain curves and associated parameters historically were based on engineering units, since starting dimensions are easily measured and incorporated into the calculations. True stress and true strain provide a much better representation of how the material behaves as it is being deformed, which explains its use in computer forming and crash simulations. Although sample dimensions are challenging to measure during a tensile test, there are equations that relate engineering units to true units. Conventional stress-strain curves generated in engineering units can be converted to true units for inclusion in simulation software packages.

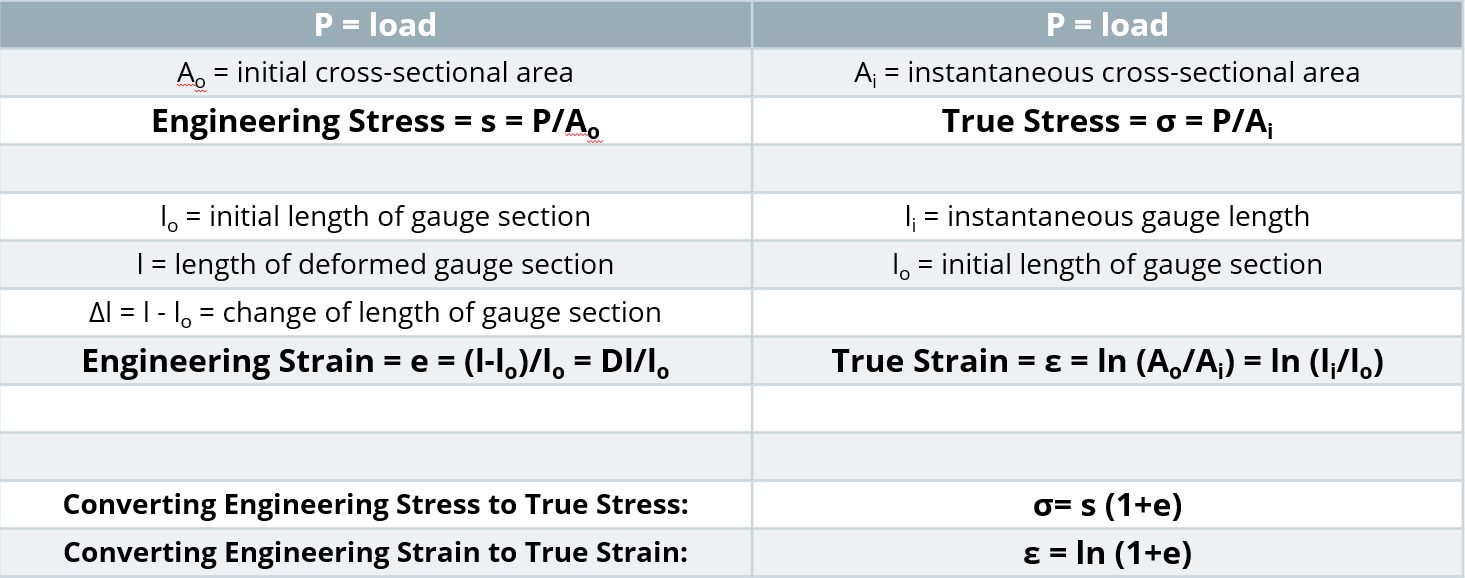
Relationships Between Engineering and True Properties

Global vs Local Formability

Formability

Most sheet metals have different “Global” and “Local” forming capabilities, so it is critical to understand their meaning to optimize grade selection, processing, and usage.

Historically, most fabricators needed to consider only global formability when designing and stamping parts. Drawing, plane-strain tension, and stretch forming are “global” forming modes where deformation occurs in the plane of the sheet over relatively large regions of material. Tensile failures or necking failures, where the steel progressively thins during forming, are a characteristic of global formability failures. The strains across a stamped part start low and evenly distributed but begin to concentrate as the punch approaches bottom-dead-center. Critical thinning (also called necking) occurs if the strains induced by the part shape and forming process exceed the forming limit of the chosen sheet metal. Forming simulation software packages have reliably shown the ability to accurately predict global formability concerns and hot spots with the use of inputs like tensile test data and the correct forming limit curve.

Local formability failure modes are an entirely different failure condition, where fractures occur out of the plane of the sheet in response to concentrated deformation created when forming localized features like stretch flanges, extruded holes, or bends around a radius too small for the selected steel grade. These failures typically occur without any observable thinning or necking (Figure 1). Forming simulation software that considers only the forming limit curve or maximum thinning as the failure criteria cannot predict local formability failures.

$Figure 1: A fracture related to insufficient local formability. Note the lack of thinning near the fracture.$

Figure 1: A fracture related to insufficient local formability. Note the lack of thinning near the fracture. ^H-5

Cutting conditions and edge stresses developed in blanking and slitting operations play a significant role in limiting local formability. Trim steel clearances, shear angles, trim steel materials, tool sharpness and design, steel rolling direction, and part design considerations are all important (Figure 2).

Figure 2: Cut edge uniformity influences edge quality.^U-6

The absence of global thinning leading to the onset of localized necking highlights the importance of clearly defining the actual mode of failure before trying to identify possible solutions. Examination of the edge of the part where the failure is occurring is the best way to accomplish this. Figure 3 shows a photo of a typical local formability related edge fracture where no observable thinning/necking before fracture occurs.

$Figure 3: A typical local formability edge fracture viewed from different angles, with no appreciable thinning prior to fracture.U-6$

Figure 3: A typical local formability edge fracture viewed from different angles, with no appreciable thinning prior to fracture.^U-6

Some AHSS grades are more prone to these local formability failures. A reduced hardness difference between microstructural phases appears to improve local formability. At a given tensile strength level, there may be grades with improved global formability, improved local formability, or a balanced approach available. Choosing the optimum grade requires understanding of the manufacturing die process and the functionality requirements associated with the part and its application.

Figure 4 shows an edge fracture on a DP980 rocker panel. This panel experienced edge fractures during production, occurring in embossments along the edge of the part, with no evidence of necking at the fracture site. This is a classic local formability failure, reinforcing the need to inspect the conditions at the fracture zone of AHSS to determine whether the root failure is global or local formability. Process and die solutions differ based on the mode of failure.

$Figure 4: Classic local formability related edge fracture on an embossment within a DP980 part.U-6$

Figure 4: Classic local formability related edge fracture on an embossment within a DP980 part.^U-6

Grade dependency is highlighted in Figure 5, which compares edges of HSLA 50SK on the left and DP500Y/780T on the right after stretch-bend testing under conditions to produce fracture. The HSLA sample shows the characteristic thinning down associated with necking. The DP steel did not have a visible neck at the failure location.^S-11

$Figure 5: Left: HSLA 50SK, showing thinning at the fracture location, which is typical for global formability failures Right: DP 500Y/780T, showing no thinning at the fracture location, which is typical for local formability failures.S-11$

Figure 5: Left: HSLA 50SK, showing thinning at the fracture location, which is typical for global formability failures. Right: DP 500Y/780T, showing no thinning at the fracture location, which is typical for local formability failures.^S-11

Mechanical tests now being employed to better quantify and characterize the unique local formability related failure modes associated with AHSS include:

Fracture-Limited Formability = Local Formability

In general, most sheet metal stamping failures result from exceeding the necking limit, and are termed global formability failures. However, there are important conditions which promote fracture before first developing a neck. These are of particular concern since such fractures cannot be predicted or anticipated based on conventional FLC and grid strain analysis techniques. Recent advances in metal forming software codes now allow input of appropriate data which substantially aids in these efforts. Still, there is no universally accepted shape of the Fracture Limit Curve.

Local Formability: Bending

Researchers discovered that all the steel through the sheet thickness must exceed the forming limit for necking to begin. In tight bends where the inner surface is compressed, strains never reach the critical strains in the conventional forming limit curve, which is why necking is not seen on the outer bend surface above a critical r/t level, or the ratio between the radius and the thickness.

However, as strength increases, the fracture limit is closer to the necking limit determined by the FLC. Advanced High Strength Steels are even more sensitive to local formability failures due to the localization of strains which occur at the interface between hard and soft phases in the microstructure.

On thin, wide sheet, bending strains on the metal surface plot along the axis of plane strain. The Fracture Limit Curve in this location is higher than the necking Failure Limit Curve, but since the critical strains only need to be reached on the outermost surface, higher-strength steels have a greater risk of experiencing bending fractures. In these cases, the material fracture limit becomes the effective forming limit in deformation modes with severe through-thickness strain gradients, and this is not considered in the traditional FLD.

Local Formability: Sheared Edge Expandability (Hole Expansion)

In a hole expansion test, the strains at the edge of the expanding hole follow a uniaxial strain path until reaching the fracture limit. In lower-strength steels with clean, machined (undamaged) edges, expansion ratios over 300% might be possible. As mentioned above, higher-strength steels have a lower fracture limit. Still, undamaged machined edges provide the best conditions for high hole expansion.

Cutting operations like blanking, shearing, and punching all damage the edge and lowers the fracture limit, meaning that the fracture limit might be reached at even lower strains. Strain localization occurring at the interface between hard and soft microstructural phases highlight why some grades have still lower critical strains.

Figure 6 caption: Higher strength steels have a smaller gap between the necking Forming Limit Curve and the Fracture Limit Curve.

Figure 6: Higher-strength steels have a smaller gap between the necking Forming Limit Curve and the Fracture Limit Curve.

Summary of Global Formability

The resistance to localized thinning (necking) is the key to global formability.
Stamped parts get progressively thinner as the press stroke approaches bottom-dead-center. Rapid thinning in critical areas lead to the onset of localized necking. Global formability promotes the ability to reach deeper draw depths before initiation of necking.
Measures of global formability include the work-hardening exponent (n-value), the uniform elongation value, and the total elongation value determined in a tensile test, along with the forming limit curve (FLC).
Global formability failures occur when a through-thickness volume of the formed sheet steel exceeds this forming limit and begins to neck.
Necking failure typically should not occur if the global formability limit is exceeded on only the outer surface of steel bent over a radius or expanded at a cut edge and not through the full thickness of the metal.
Uniform elongation measures the resistance to local necking. The global formability limit corresponds to Uniform Elongation in the strain state achieved in a tensile test sample. The Forming Limit Curve (FLC) encompasses all strain states.
For mild and conventional high strength steels, there is a large difference between the necking limit and the ultimate fracture limit. This corresponds to the difference between Uniform Elongation and Total Elongation in a tensile test, where the value of total elongation is typically twice that of uniform elongation.

Summary of Local Formability

The resistance to fracture is the key to local formability.
Local formability promotes fracture resistance in response to creating local product features like stretch flanges, extruded holes, and tight-radius bends.
Local formability tests which evaluate the stretchability of appropriately prepared edges by deforming them with a punch may have limited reproducibility between labs due to the influence of different sample preparation methods. Determining parameters like True Fracture Strain, Reduction in Area at Fracture, or Thickness Strain at Fracture with a well-defined tensile test typically results in repeatable and reproducible values.
Local formability failure occurs when strains at the surface or edge exceed the ultimate fracture limit, a value that is higher than the necking limit determined by the Forming Limit Curve.
Local formability failures occur more frequently on higher strength steels partly because of a smaller difference between the necking limit determined by the Forming Limit Curve and ultimate fracture limit.
Work hardening and damage from edge preparation methods like shearing further reduce edge formability to values typically lower than indicated by the Forming Limit Curve, especially for AHSS. The strain localization at the interface between hard and soft phases in AHSS also contribute to an increased risk of local formability failures.
The lack of a localized neck is a characteristic trait associated with of local formability failures.

« Older Entries

Next Entries »