Simulation Inputs
- Yield Criteria
- Hardening Curve
- Failure Conditions
- Constitutive Laws and Their Influence on Forming Simulation Accuracy
- Testing to Determine Inputs for Simulation
- Application of Advanced Testing to Failure Predictions
Predicting metal flow and failure is the essence of sheet metal forming simulation. Characterizing the stress-strain response to metal flow requires a detailed understanding of when the sheet metal first starts to permanently deform (known as the yield criteria), how the metal strengthens with deformation (the hardening law), and the failure criteria (for example, the forming limit curve). Complicating matters is that each of these responses changes as three-dimensional metal flow occurs, and are functions of temperature and forming speed.
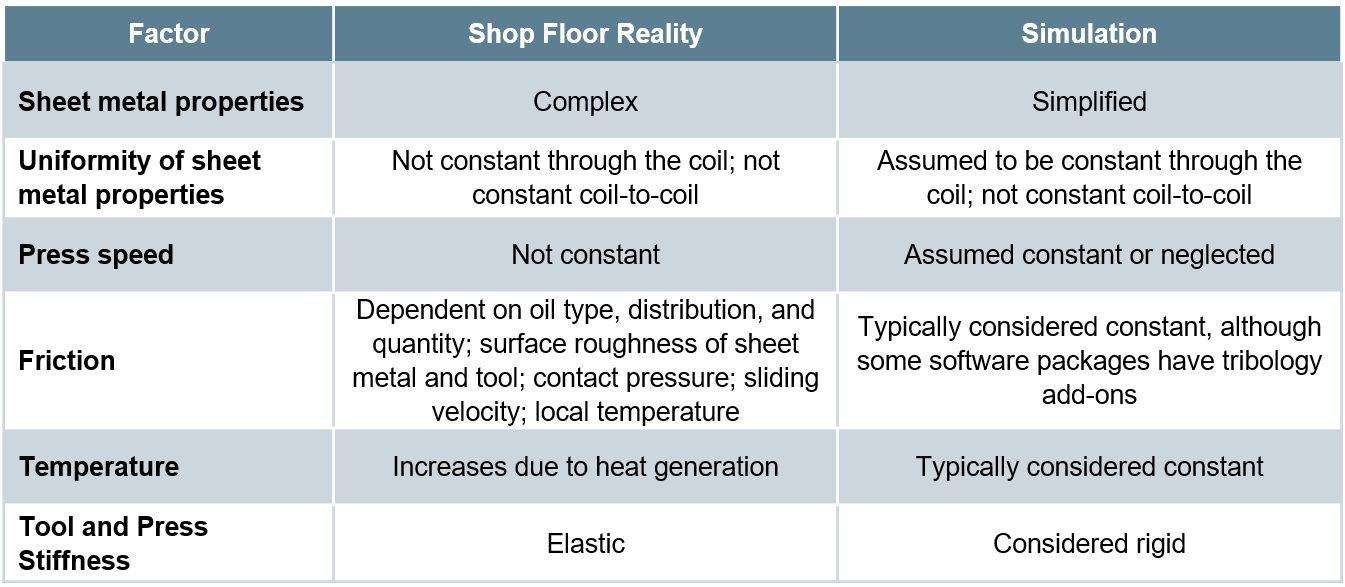
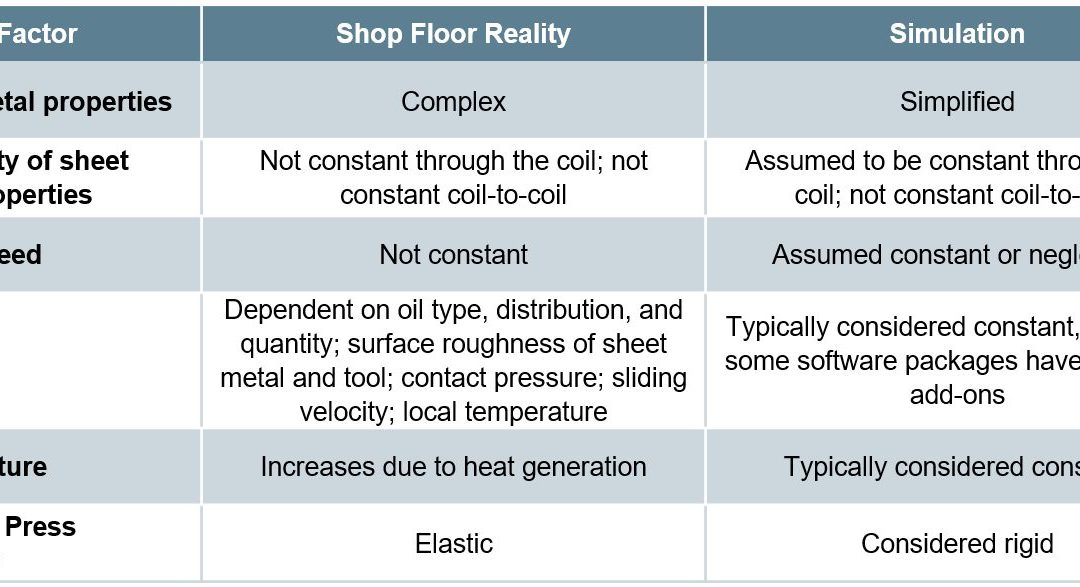
The ability to simulate these features reliably and accurately requires mathematical constitutive laws that are appropriate for the material and forming environments encountered. Advanced models typically improve prediction accuracy, at the cost of additional numerical computational time and the cost of experimental testing to determine the material constants. Minimizing these costs requires compromises, with some of these indicated in Table I created based on Citations B-16 and R-28.
Yield Criteria
The yield criteria (also known as the yield surface or yield loci) defines the conditions representing the transition from elastic to plastic deformation. Assuming uniform metal properties in all directions allows for the use of isotropic yield functions like von Mises or Tresca. A more realistic approach considers anisotropic metal flow behavior, requiring the use of more complex yield functions like those associated with Hill, Barlat, Banabic, or Vegter.
No one yield function is best suited to characterize all metals. Some yield functions have many required inputs. For example, “Barlat 2004-18p” has 18 separate parameters leading to improved modeling accuracy – but only when inserting the correct values. Using generic textbook values is easier, but negates the value of the chosen model. However, determining these variables typically is costly and time-consuming, and requires the use of specialized test equipment.
Hardening Curve
Metals get stronger as they deform, which leads to the term work hardening. The flow stress at any given amount of plastic strain combines the yield strength and the strengthening from work hardening. In its simplest form, the stress-strain curve from a uniaxial tensile test shows the work hardening of the chosen sheet metal. This approach ignores many of the realities occurring during forming of engineered parts, including bi-directional deformation.
Among the simpler descriptions of flow stress are those from Hollomon, Swift, and Ludvik. More complex hardening laws are associated with Voce and Hockett-Sherby.
The strain path followed by the sheet metal influences the hardening. Approaches taken in the Yoshida-Uemori (YU) and the Homogeneous Anisotropic Hardening (HAH) models extend these hardening laws to account for Bauschinger Effect deformations (the bending-unbending associated with travel over beads, radii, and draw walls).
As with the yield criteria, accuracy improves when accounting for three-dimensional metal flow, temperature, and forming speed, and using experimentally determined input parameters for the metal in question rather than generic textbook values.
Failure Conditions
Defining the failure conditions is the other significant challenge in metal forming simulation. Conventional Forming Limit Curves describe necking failure under certain forming modes, and are easier to understand and apply than alternatives. Complexity and accuracy increase when accounting for non-linear strain paths using stress-based Forming Limit Curves. Necking failure is not the only type of failure mode encountered. Conventional FLCs cannot predict fracture on tight radii and cut edges, nor can they account for dimensional issues like springback. For these, failure criteria definitions which are more mathematically complex are appropriate.
Constitutive Laws and Their Influence
on Forming Simulation Accuracy
Many simulation packages allow for an easy selection of constitutive laws, typically through a drop-down menu listing all the built-in choices. This ease potentially translates into applying inappropriate selections unless the simulation analyst has a fundamental understanding of the options, the inputs, and the data generation procedures.
Some examples:
- The “Keeler Equation” for the estimation of FLC0 has many decades of evidence in being sufficiently accurate when applied to mild steels and conventional high strength steels. The simple inputs of n-value and thickness make this approach particularly attractive. However, there is ample evidence that using this approach with most advanced high strength steels cannot yield a satisfactory representation of the Forming Limit Curve.
- Even in cases where it is appropriate to use the Keeler Equation, a key input is the n-value or the strain hardening exponent. This value is calculated as the slope of the (natural logarithm of the true stress):(natural logarithm of the true strain curve). The strain range over which this calculation is made influences the generated n-value, which in turn impacts the calculated value for FLC0.
- The strain history as measured by the strain path at each location greatly influences the Forming Limit. However, this concept has not gained widespread understanding and use by simulation analysts.
- A common method to experimentally determine flow curves combines tensile testing results through uniform elongation with higher strain data obtained from biaxial bulge testing. Figure 1 shows a flow curve obtained in this manner for a bake hardenable steel with 220 MPa minimum yield strength. Shown in Figure 2 is a comparison of the stress-strain response from multiple hardening laws associated with this data, all generated from the same fitting strain range between yield and tensile strength. Data diverges after uniform elongation, leading to vastly different predictions. Note that the differences between models change depending on the metal grade and the input data, so it is not possible to say that one hardening law will always be more accurate than others.
Figure 1: Flow curves for a bake hardenable steel generated by combining tensile testing with bulge testing.L-20
Figure 2: The chosen hardening law leads to vastly different predictions of stress-strain responses.L-20
- Analysts often treat Poisson’s Ratio and the Elastic Modulus as constants. It is well known that the Bauschinger Effect leads to changes in the Elastic Modulus, and therefore impacts springback. However, there are also significant effects in both Poisson’s Ratio (Figure 3) and the Elastic Modulus (Figure 4) as a function of orientation relative to the rolling direction. Complicating matters is that this effect changes based on the selected metal grade.
Figure 3: Poisson’s Ratio as a Function of Orientation for Several Grades (Drawing Steel, DP 590, DP 980, DP 1180, and MS 1700) D-11
Figure 4: Modulus of Elasticity as a Function of Orientation for Several Grades (Drawing Steel, DP 590, DP 980, DP 1180, and MS 1700) D-11
Testing to Determine Inputs for Simulation
Complete material card development requires results from many tests, each attempting to replicate one or more aspects of metal flow and failure. Certain models require data from only some of these tests, and no one model typically is best for all metals and forming conditions. Tests described below include:
- Tensile testing [room temperature at slow strain rates to elevated temperature with accelerated strain rates]
- Biaxial bulge testing
- Biaxial tensile testing
- Shear testing
- V-bending testing
- Tension-compression testing with cyclic loading
- Friction
Tensile testing is the easiest and most widely available mechanical property evaluation required to generate useful data for metal forming simulation. However, a tensile test provides a complete characterization of material flow only when the engineered part looks like a dogbone and all deformation resulted from pulling the sample in tension from the ends. That is obviously not realistic. Getting tensile test results in more than just the rolling direction helps, but generating those still involves pulling the sample in tension. Three-dimensional metal flow occurs, and the stress-strain response of the sheet metal changes accordingly.
The uniaxial tensile test generates a draw deformation strain state since the edges are free to contract. A plane strain tensile test requires using a modified sample geometry with an increased width and decreased gauge length,
Forming all steels involves a thermal component, either resulting from friction and deformation during “room temperature” forming or the intentional addition of heat such as used in press hardening. In either case, modeling the response to temperature requires data from tests occurring at the temperature of interest, at appropriate forming speeds. Thermo-mechanical simulators like Gleeble™ generate such data.
Conventional tensile testing occurs at deformation rates of 0.001/sec. Most production stamping occurs at 10,000x that amount, or 10/sec. Crash events can be 2 orders of magnitude faster, at about 1000/sec. The stress-strain response varies by both testing speed and grade. Therefore, accurate simulation models require data from higher-speed tensile testing. Typically, generating high speed tensile data involves drop towers or Split Hopkinson Pressure Bars.
A pure uniaxial stress state exists in a tensile test only until reaching uniform elongation and the beginning of necking. Extrapolating uniaxial tensile data beyond uniform elongation risks introducing inaccuracies in metal flow simulations. Biaxial bulge testing generates the data for yield curve extrapolation beyond uniform elongation. This stretch-forming process deforms the sheet sample into a dome shape using hydraulic pressure, typically exerted by water-based fluids. Citation I-12 describes a standard test procedure for biaxial bulge testing.
A Marciniak test used to create Forming Limit Curves generates in-plane biaxial strains. Whereas FLC generation uses 100 mm diameter samples, larger samples allow for extraction of full-size tensile bars. Although this approach generates samples containing biaxial strains, the extracted samples are tested uniaxially in the conventional manner.
Biaxial tensile testing allows for the determination of the yield locus and the biaxial anisotropy coefficient, which describes the slope of the yield surface at the equi-biaxial stress state. This test uses cruciform-shaped test pieces with parallel slits cut into each arm. Citation I-13 describes a standard test procedure for biaxial tensile testing. The biaxial anisotropy coefficient can also be determined using the disk compression testing as described in Citation T-21.
Shear testing characterizes the sheet metal in a shear loading condition. There is no consensus on the specimen type or testing method. However, the chosen testing set-up should avoid necking, buckling, and any influence of friction.
V-bending tests determine the strain to fracture under specific loading conditions. Achieving plane strain or plane stress loading requires use of a test sample with features promoting the targeted strain state.
Tension-compression testing characterizes the Bauschinger Effect. Multiple cycles of tension-compression loading captures cyclic hardening behavior and elastic modulus decay, both of which improve the accuracy of springback predictions. Again, no standard procedure exists. The biggest challenge with this test is preventing buckling from occurring during in-plane compressive loading. Related to this is the need to compensate for the friction caused by the anti-buckling mechanism in the stress-strain curves .
Friction is obviously a key factor in how metal flows. However, there is no one simple value of friction that applies to all surfaces, lubricants, and tooling profiles. The coefficient of friction not only varies from point to point on each stamping but changes during the forming process. Determining the coefficient of friction experimentally is a function of the testing approach used. The method by which analysts incorporate friction into simulations influences the accuracy and applicability of the results of the generated model.
Studies are underway to reduce the costs and challenges of obtaining much of this data. It may be possible, for example, to use Digital Image Correlation (DIC) during a simple uniaxial tensile testing to quantify r-value at high strains, determine the material hardening behavior along with strain rate sensitivity, assess the degradation of Young’s Modulus during unloading, and use the detection of the onset of local neck to help account for non-linear strain path effects.S-110
Application of Advanced Testing to Failure Predictions
Global formability failures occur when the forming strains exceed the necking forming limit throughout the entire thickness of the sheet. Advanced steels are at risk of local formability failures where the forming strains exceed the fracture forming limit at any portion of the thickness of the sheet.
Fracture forming limit curves plot higher than the conventional necking forming limit curves on a graph showing major strain on the vertical axis and minor strain on the horizontal axis. In conventional steels the gap between the fracture FLC and necking FLC is relatively large, so the part failure is almost always necking. The forming strains are not high enough to reach the fracture FLC.
In contrast, AHSS grades are characterized by a smaller gap between the necking FLC and the fracture FLC. Depending on the forming history, part geometry (tight radii), and blank processing (cut edge quality), forming strains may exceed the fracture FLC at an edge or bend before exceeding the necking FLC through-thickness. In this scenario, the part will fracture without signs of localized necking.
A multi-year study funded by the American Iron and Steel Institute at the University of Waterloo Forming and Crash Lab describes a methodology used for forming and fracture characterization of advanced high strength steels, the details of which can be found in Citations B-11, W-20, B-12, B-13, R-5, N-13 and G-19.
This collection of studies, as well as work coming out of these studies, show that relatively few tests sufficiently characterize forming and fracture of AHSS grades. These studies considered two 3rd Gen Steels, one with 980MPa tensile strength and one with 1180MPa tensile.
- The yield surface as generated with the Barlat YLD2000-2d yield surface (Figure 5) comes from:
- Conventional tensile testing at 0, 22.5, 45, 67.5, and 90 degrees to the rolling direction, determining the yield strength and the r-value;
- Disc compression tests according to the procedure in Citation T-21 to determine the biaxial R-value, rb.
Figure 5: Tensile testing and disc compression testing generate the Barlat YLD2000-2d yield surface in two 3rd Generation AHSS Grades B-13
- Creating the hardening curve uses a procedure detailed in Citations R-5 and N-13, and involves only conventional tensile and shear testing using the procedure included in Citation P-15.
Figure 6: Test geometries for hardening curve generation. Left image: Tensile; Right image: Shear.N-13
- Characterizing formability involved generating a Forming Limit Curve using Marciniak data or process-corrected Nakazima data. (See our article on non-linear strain paths) and Citation N-13 for explanation of process corrections]. Either approach resulted in acceptable characterizations.
- Fracture characterization uses four plane stress tests: shear, conical hole expansion, V-bending, and a biaxial dome test. The result from these tests calibrate the fracture locus describing the stress states at fracture.
- Yield Criteria
- Hardening Curve
- Failure Conditions
- Constitutive Laws and Their Influence on Forming Simulation Accuracy
- Testing to determine inputs for simulation
- Application of Advanced Testing to Failure Predictions