Forming Modes
Stretching is the sheet metal forming process where the punch which creates the part shape forces the sheet metal to thin since lock beads prevent metal flow inward from the flange area. In contrast with drawing, significant metal thinning occurs in stretching, especially in the biaxial tension mode. The biaxial increase in surface area reduces the metal thickness, maintaining the constancy of volume. The thinning soon reaches the onset of the local neck and failure as defined by the appropriate forming limit curve. The steel property that improves stretching is the strain hardening exponent, or n-value.
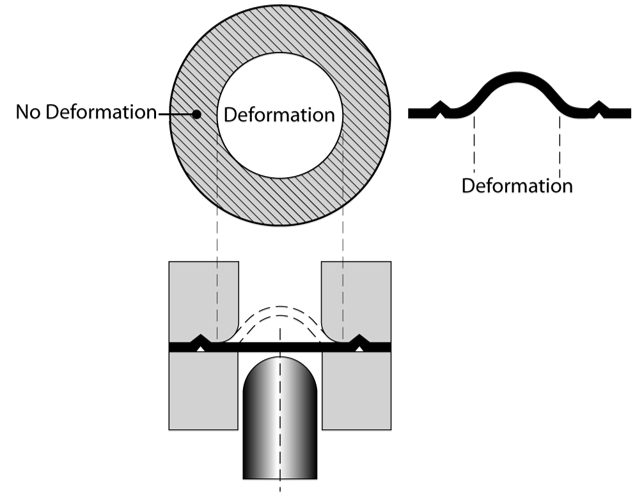
Stretchability, or the ability for a sheet metal to be stretched with no metal flowing from the flange or binder, often is assessed by the hemispherical dome test. Here, a hemispherical punch (usually with a 100 mm diameter) deforms a fully clamped blank. This ensures pure biaxial stretch without metal flowing from the blank into the deformation zone (Figure 1).

Figure 1: Stretch forming generated by a hemispherical punch stretching a locked circular blank.
Comparing the ratio of maximum dome height to punch diameter (H/d) is one way to view the results. Figure 2 illustrates a typical test output. Note the maximum dome height (H/d) at failure decreased as the yield strength increased and the n-value decreased.

Figure 2: Dome stretch tests of 1mm thick steel using a 100 mm hemispherical punch and a clamped blank.C-9
Additional stretch tests are possible with the hemispherical dome tester other than the dome height at failure shown in Figure 2. The limiting dome height (LDH) test stretches a rectangular steel strip which is locked in the longitudinal direction (Figure 3). Typically, a conventional rust preventive oil coats the blanks. Strips of different width are tested, with a circular lock bead preventing metal flow from the binder in the regions where the blank dimensions are large enough. The output of this test is the maximum dome height at failure. Figure 3 shows the achievable hemispherical dome height is substantially higher for the TRIP steel compared to the HSLA steel grade of equivalent tensile strength.
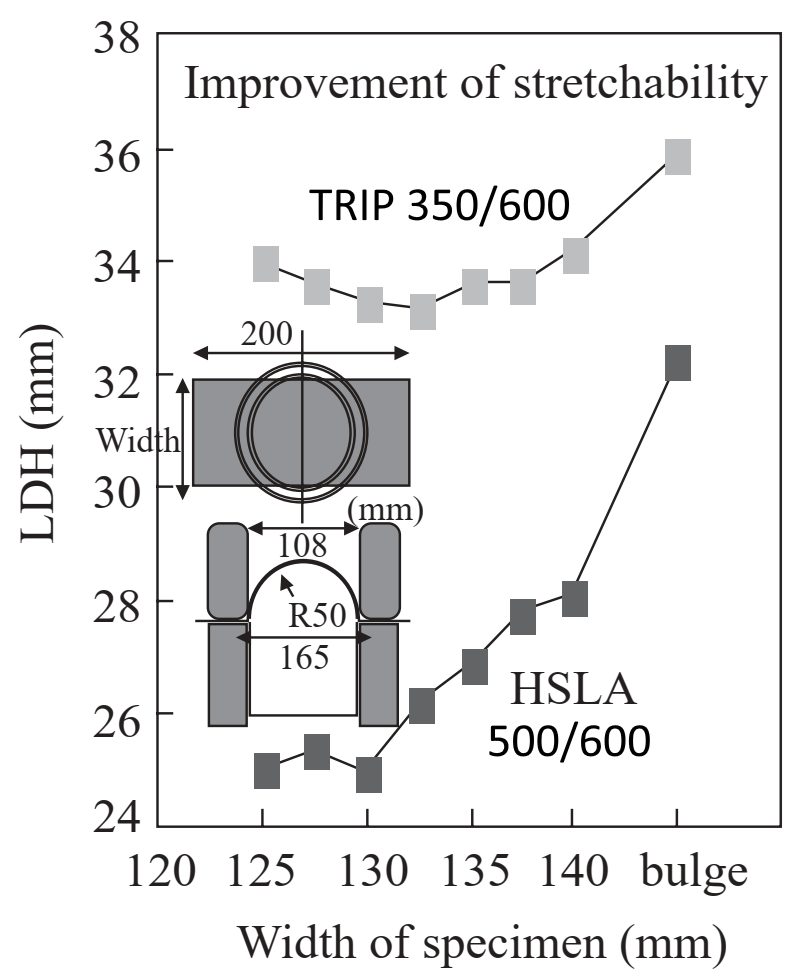
Figure 3: Limiting Dome Height is greater for TRIP than HSLA at the same tensile strength.T-2
The same tooling, steels, and lubricant from Figure 3 generated the thinning strains in Figure 4. Instead of forming to failure, the 50 mm radius hemispherical punch stretched the dome height to only 25 mm for both steels. The high n-value of TRIP steels minimizes strain gradients and reduces localizes thinning, helping to delay necking and form more complex geometries.
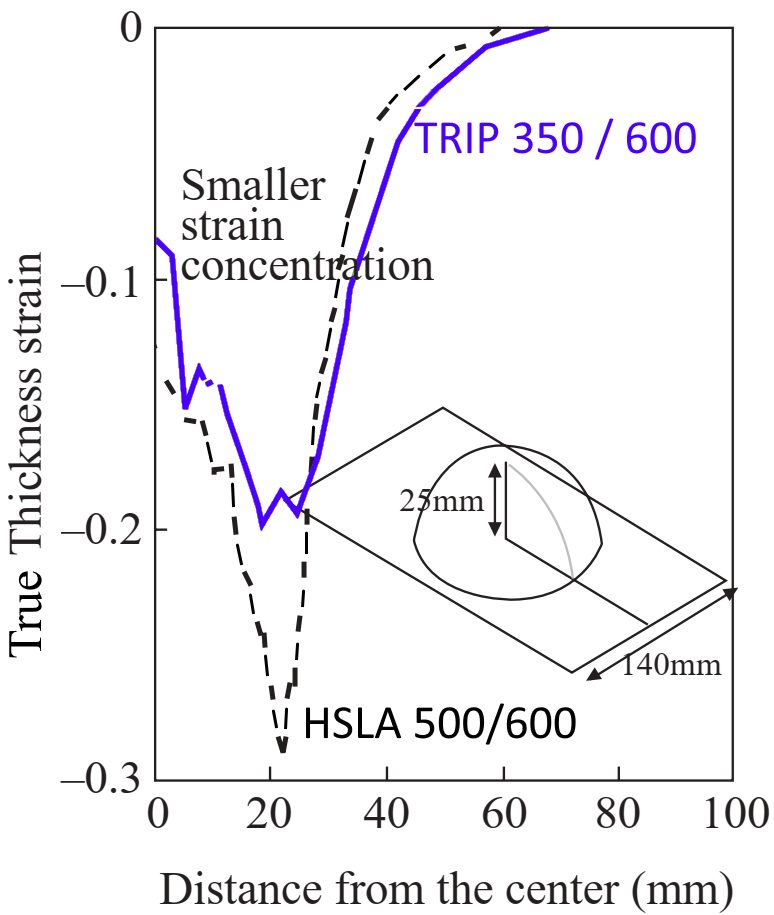
Figure 4: TRIP steel experiences less thinning than HSLA steel of the same tensile strength when formed to a constant dome height.T-2
The Limiting Dome Height test results for EDDS (vacuum-degassed interstitial-free) steel and three Advanced High Strength Steel grades are in Figure 5. Instead of plotting the various dome heights (as in Figure 3) to find the minimum value, Figure 5 simply shows the minimum value for each steel. TWIP (Twinning Induced Plasticity) steel has unique properties for stretchability and total elongation. Stretchability exceeds even that of EDDS IF steel.
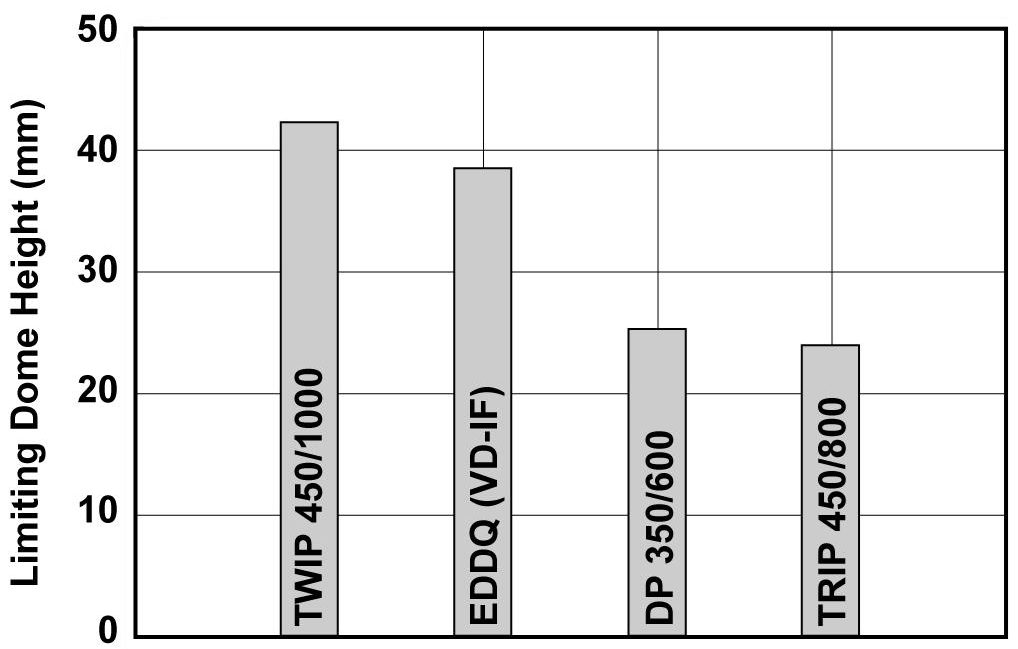
Figure 5: Limiting Dome Height values reflect relative stretchability of three AHSS compared with a low strength IF steel.P-2
![Bending]()
Forming Modes
top-of-page
The usual mode of bending is curvature around a straight-line radius (Figure 1). Through the thickness is a gradient of strains from maximum outer fiber tension (the outermost surface) through a neutral axis to inner fiber compression (the surface closest to the punch or bend axis). No strain occurs along the bend axis in the direction parallel to the bend axis, and therefore is in plane strain. The discussion below considers only bulk deformation, and excludes the implications of any edge effects. Bend testing procedures are linked here.

Figure 1: Typical bend where the outer surface is in tension, and the inner surface is in compression. A neutral axis lies in between.S-23
When sheet metal flows through draw beads or over the die radius into the punch opening, it is bent, straightened, and in the case of draw beads re-bent in the opposite direction. The net strain after this process may be relatively small. However, each of the sequential bending and unbending steps strain hardens the sheet metal, which reduces the ability for further deformation of the metal in subsequent operations.
Deformation at the outer surface during three-point bending depends on the stretchability capacity of the metal. The failure strain in the bend is related to the total elongation of conventional steel, but AHSS grades with multiphase microstructures such as DP and TRIP experience shear fracture that severely reduces the bendability before failure occurs. A higher total elongation helps sustain a larger outer fiber stretch of the bend before surface fracture, thereby permitting a smaller bend radius. Since total elongation decreases with increasing strength for a given sheet thickness, the minimum design bend radius must be increased (Figure 2).

Figure 2: Larger bend radius is needed as the total elongation decreases.S-23
The ratio of punch radius to sheet thickness, or the r/t ratio, allows for calculation of the amount of elongation on the outermost surface. This value can be compared against the total elongation of the metal as determined in a tensile test, or against the minimum elongation value allowed in the specification. If the part geometry will not allow for sufficient elongation for the selected metal grade, then either the part, process, or steel grade must change. [Note that this is not a perfect assessment, since elongation in a tensile test is measured relative to a 50 or 80 mm gauge length, which is likely different than the dimensions of the bent section.]
For design and springback control, usually a smaller r/t ratio is desirable. However, this may not be suitable in terms of formability. Increased material strength usually is associated with a reduction in total elongation, which in turn means a successful bend requires a larger r/t ratio.
For equal strengths, most AHSS grades have higher total elongations than conventional HSLA steels. However, several AHSS grades have limited local formability based on their microstructure, and may be at risk for cracking during edge expansion.
Cracking in production stamping conditions at stress levels below what is predicted with Forming Limit Diagrams may be attributed to these local formability failures. As an illustration, physical bend tests and simulations were performed for both HSLA and DP780 steels.S-11 The HSLA global formability failure aligned with simulation predictions (Figure 3), and was accompanied by a visible neck (Figure 4). In contrast, the DP780 showed no visible neck at the failure site (Figure 5) and no correlation between the simulation and actual test results (Figure 6).
Like hole expansion, bending limits in AHSS products are further lowered by shear fracture associated with the interfaces between the ductile ferrite and the hard martensite phase in the microstructure. This reduction becomes more severe as the strength increases, since increasing strength is achieved by increasing the volume of the hard martensite phase. More about shear fracture is found here.

Figure 3: Forming simulation of HSLA with strong correlation to actual testing.S-11

Figure 4: Close-up of visible necking before tensile failure in HSLA.S-11

Figure 5: Comparison of forming simulation with actual testing of the DP780. Note lack of correlation.S-11

Figure 6: Close-up of local formability failure on DP780 with no visible necking before failure.S-11
Rotary Bending
One way to address springback involves the use of rotary benders. Rotary benders transfer the vertical movement of a press stroke into a precise, rotary forming motion. A rocker or rotating die can simultaneously hold, bend, and overbend the sheet past 90° to counter material springback (Figure 7).
Figure 7: The rotation of the rocker bends the sheet metal around the anvil with less pressure than needed for wipe toolsD-8
Use rotary bending tooling where possible instead of flange wipe dies. Rotary bending allows for easy adjustment of the bending angle to correct for changes in springback due to variations in steel properties, die set, lubrication, and other process parameters. In addition, the tensile loading generated by the wiping shoe is absent.
There are four sequential steps to the process:
1) Downward pressure from the rocker clamps the part with the bending lobes before bending starts
2) Induced rotation of the rocker bends material around the anvil
3) The rocker bends the sheet metal past final angle to compensate for springback
4) The rocker releases the sheet metal to allow springback to desired angle
Using rotary benders to roll darts into the part during bending provides another way to reduce springback and stiffen the part (Figure 8).

Figure 8: Stiffening darts can be created as part of the rotary bending operation.R-7
Back to the Top
![Bending]()
Forming Modes
Drawing is the sheet metal forming process where the punch that creates the part shape forces the sheet metal to pull in from the flange area. In contrast with stretch-drawing or stretch forming, little metal thinning occurs in pure drawing. There is not a generally accepted definition for the term “deep drawing,” although some references describe it as when the depth of draw is greater than the diameter.
Drawability, or the ability for a sheet metal to be drawn into a cup, is assessed by the cup drawing test to measure the Limiting Draw Ratio, or LDR. Here, a cylindrical punch contacts and then pushes a circular blank into the die (Figure 1). The ratio of the largest blank diameter successfully drawn into a cup to the punch diameter used for drawing is the LDR.

Figure 1: In the cup drawing test, a punch deforms a circular blank into a cylindrical cup. The largest ratio of blank diameter to punch diameter successfully drawn into a cup is the Limiting Draw Ratio (LDR).
In the LDR test, metal in the circular blank flows over the die radius and into the cup wall. The metal movement from the flat blank to the vertical sidewalls is the only metal movement which happens, since there is no metal flow within the flat bottom region.
As shown in Figure 2, the flange of the circular blank undergoes radial tension and a circumferential compression as the flange moves in a radial direction towards the circular die radius in response to a pull generated by a flat bottom punch. Blank holder pressure is set to prevent buckles in the blank.
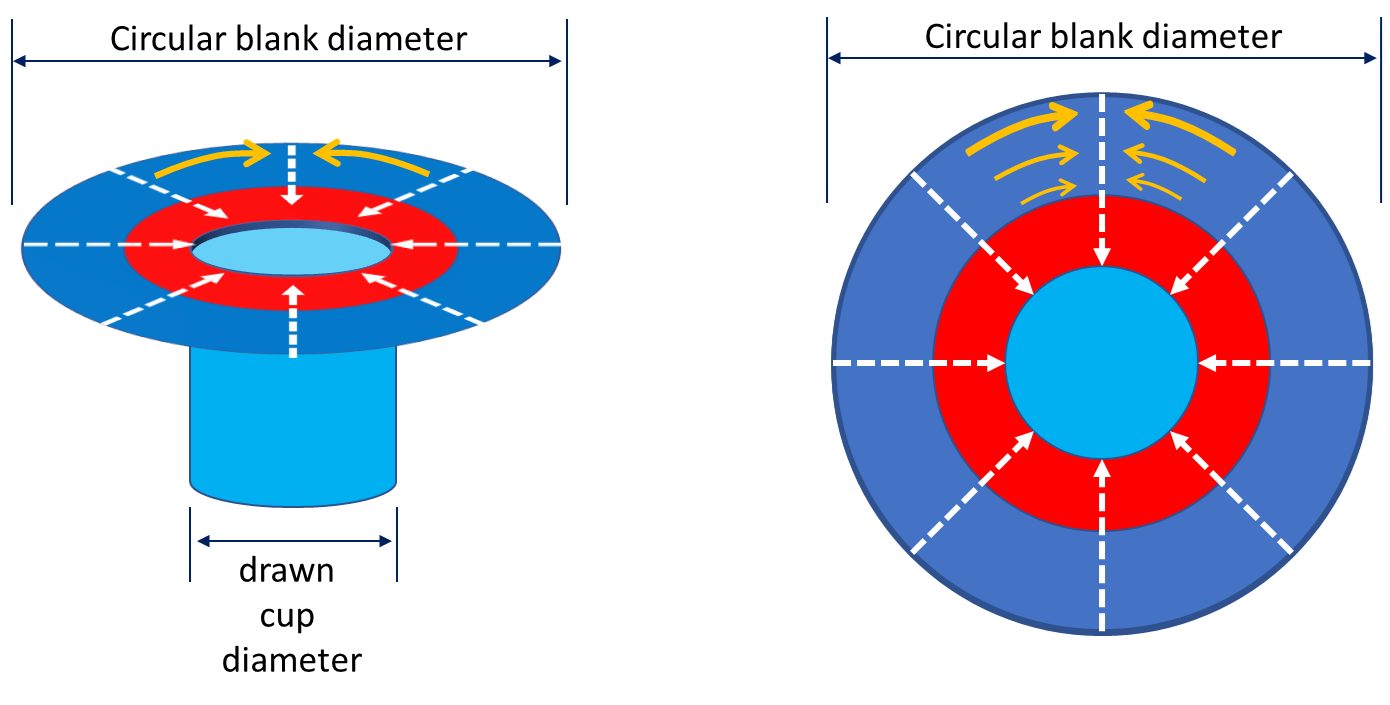
Figure 2: Tension and compression in a drawn cup. Dashed white arrows indicate the radial tension created during cup forming; orange arrows indicate flange compression as a greater amount of metal feeds into progressively smaller regions.
The steel property that improves cup drawing or radial drawing is the normal anisotropy or rm value. Values greater than 1 increase in the Limiting Draw Ratio. In contrast, the LDR is insensitive to the strength of the steel and the n-value. High-strength steels with UTS greater than 450 MPa and hot-rolled steels have rm values approximating one and LDR values between 2.0 – 2.2. Therefore, DP and HSLA steels have similar LDR values. However, TRIP steels have a slightly improved LDR deep drawability.T-2 Since the transformation of retained austenite to martensite is influenced by the deformation mode (Figure 3), the amount of transformed austenite to martensite generated by shrink flanging in the flange area is less than the plane strain deformation in the cup wall. This difference in transformation from retained austenite to martensite makes the wall area stronger than the flange area, thereby increasing the LDR. The benefit of the increased LDR is seen in Figure 4 which shows cups formed from different grades having the same tensile strength.

Figure 3: The cup wall in plane strain strengthens more than the shrink flange due to increased amounts of transformed martensite in TRIP steels.T-2

Figure 4: Cups formed from 590MPa tensile strength steels, highlighting greater draw depths possible with TRIP steels.T-2
In a study of different gradesC-9, laboratory cup drawing experiments show an approximate LDR of 2.0 – 2.2 for the DP steels tested (Figure 5). Note that a doubling of the yield strength has no effect on the LDR. An increased rm value of mild steel created a small increase in LDR over DP steel. The LDR of the MS (martensitic) steel evaluated may have been impacted by the reduced bendability going over the die radius. Figure 6 shows the cup draw depths possible for the grades reported in Figure 5.S-26
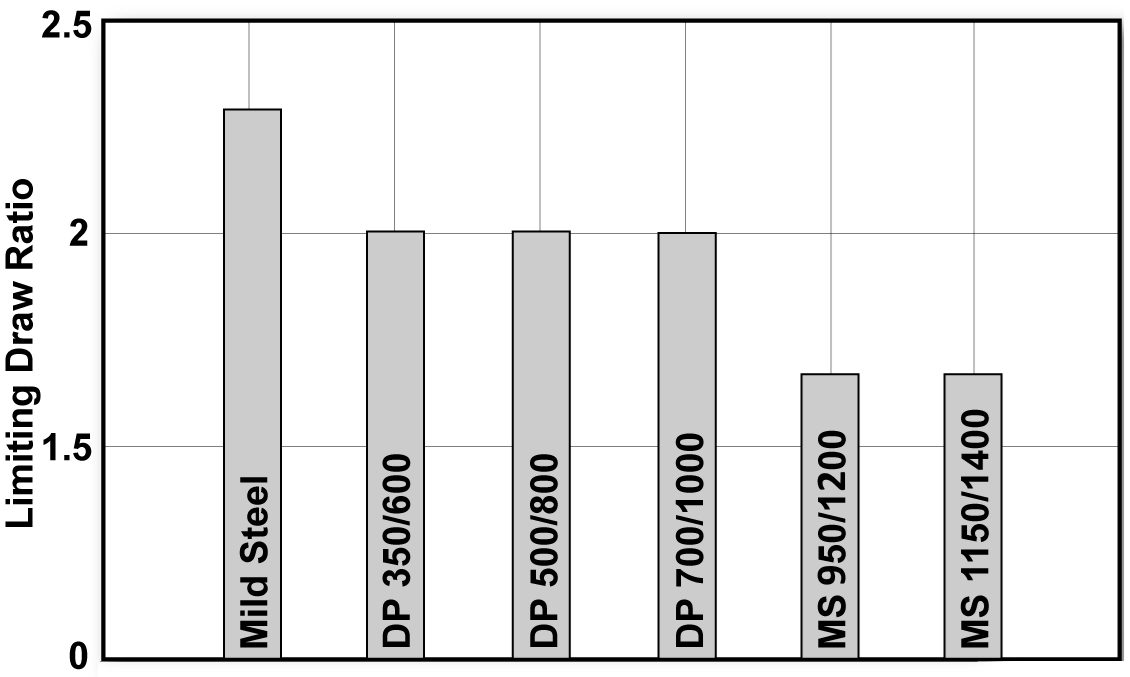
Figure 5: LDR tests for Mild, DP, and MS steels.C-9

Figure 6: Cups used in the testing reported in Figure 5.S-26
Even though r-value is the only steel property influencing the formability of drawn flat-bottom cups through its relationship with LDR, not all cups have flat bottoms. Some have hemispherical or other configurations for bottoms. Adding a dome-like shape to the cup results in a more complex forming operation which is now sensitive to material properties like n-value and microstructures.
Corners of box-shaped stampings and the ends of closed channels contain design features similar to drawn cups, providing insight on an analytical approach.
- The four corners of a box-shaped drawn panel should each be analyzed as one-quarter of a cup. Buckles forming in the binder area indicate compressive flow. The corners of the blank will form the same as a deep drawn cup.
- The side walls are formed by metal flowing from the binder across the die radius. The term for this metal flow is bend-and-straighten.
In summary, higher LDR values are achievable in steels with greater values of the normal anisotropy ratio, rm. The absolute value of the LDR, however, also depends on the lubrication, blank holder load, die radius and other system inputs. Figure 7 compares a higher viscosity lubricant on the left with a lower viscosity lubricant on the right.S-26 Die radii need to be balanced: large radii promotes metal flow and may lead to wrinkles, while small radii restricts metal flow and may lead to splits.

Figure 7: The influence of lubricant viscosity on drawing. The cup formed with the higher viscosity lubricant is on the left.S-26

Forming Modes
Stamping and die designers are interested in the forming capabilities of the steels they specify. Complex stampings are created from several different basic forming modes, which are sensitive to different mechanical properties. For this reason, steel formability, especially for AHSS grades, cannot be characterized by a single number, but instead must be done for each basic forming mode.
Forming modes and key points include:
Stretching
- Stretching is the sheet metal forming process where the punch which creates the part shape forces the sheet metal to thin since lock beads prevent metal flow inward from the flange area.
- The steel property that improves stretching is the strain hardening exponent, or n-value.
- Dome testing characterizes stretchability.
- Higher n-values flatten strain gradients, reduce localized thinning that leads to early failure, and allows the forming of more complex parts.
Bending
- Tensile testing cannot be used to determine bendability, since these are different failure modes. Different bend tests characterize bendability.
- The failure strain in the bend is related to the total elongation of conventional steel, but are limited by other issues in AHSS grades.
- For equal strengths, most AHSS grades have higher total elongations than conventional HSLA steels. However, several AHSS grades have limited local formability based on their microstructure, and may be at risk for cracking during edge expansion. AHSS grades with multiphase microstructures such as DP and TRIP experience shear fracture that severely reduces the bendability before failure occurs.
Drawing
- Drawing is the sheet metal forming process where the punch that creates the part shape forces the sheet metal to pull in from the flange area.
- The steel property that improves cup drawing or radial drawing is the normal anisotropy or rm value.
- The Limiting Draw Ratio (LDR) characterizes cup drawability.
- Higher r-value increases the LDR, but the absolute value of the LDR also depends on the lubrication, blank holder load, die radius and other system inputs.












