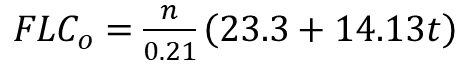FLD Archives - AHSS Guidelines

Forming Limit Curves (FLC)

topofpage

Generating Forming Limit Curves from Equations
Experimental Determination of Forming Limit Curves
Differences between Forming Limit Curves and Forming Limit Diagrams

If all stampings looked like a tensile dogbone and all deformation was in uniaxial tension, then a tensile test would be sufficient to characterize the formability of that metal. Obviously, engineered stampings are much more complex. Although a tensile test characterizes one specific strain path, a Forming Limit Curve (FLC) is necessary to have a map of strains indicating the onset of critical through-thickness necking for different linear strain paths. The strains which make up the FLC represent the limit of useful deformation. Calculations of safety margins are based on the FLC (Figure 1).

Figure 1: General graphical form of the Forming Limit Curve.^E-2

Picturing a blank covered with circles helps visualize strain paths. After forming, the circles turn into ellipses, with the dimensions related to the major and minor strains. This forms the basis for Circle Grid Strain Analysis.

Generating Forming Limit Curves from Equations

Pioneering work by Keeler, Brazier, Goodwin and others contributed to the initial understanding of the shape of the Forming Limit Curve, with the classic equation for the lowest point on the FLC (termed FLC₀) based on sheet thickness and n-value. Dr. Stuart Keeler was the Technical Editor of these AHSS Guidelines through Version 6.0, released in 2017.

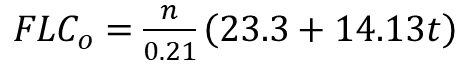Equation 1

These studies generated the left hand side of the FLC as a line of constant thinning in true strain space, while the right hand side has a slope of +0.6, at least through minor (engineering) strains of 20%.

Evidence accumulated over many decades show that this approach to defining the Forming Limit Curve is sufficient for many applications of mild steels, conventional high strength steels, and some lower strength AHSS grades like CR340Y/590T-DP. However, this basic method is insufficient when it comes to creating the Forming Limit Curves for most AHSS grades and every other sheet metal alloy. Grades with significant amounts of retained austenite experience significant deviations from these simple estimates.^H-23, ^S-61 In these cases, the FLC must be experimentally determined.

Additional studies found correlation with other properties including total elongation, tensile strength, and r-value^R-8, ^P-19, ^G-23,^A-45, ^A-46, ^H-23 with some of these attempting to define the FLC by equations.

Experimental Determination of Forming Limit Curves

ASTM ^A-47and ISO^I-16have published standards covering the creation of FLCs. Even within these standards, there are many nuances left for interpretation, primarily related to the precise definition of when a neck occurs and the associated limiting strains.

There are two steps in creating FLCs: Forming the samples and measuring the strains.

Forming sheet specimens of different widths uses either a hemispherical dome (Nakajima or Nakazima method ^N-14) or a flat-bottom punch (Marciniak method ^M-22) to generate different strain paths from which critical strains are determined. The two methods are not identical due to the different strain paths generated from the punch shape. These differences may not be significant for many lower strength and conventional High-Strength Steels, but may deviate from each other at higher strengths or with advanced microstructures. Figure 2 highlights samples formed with the Nakajima method.

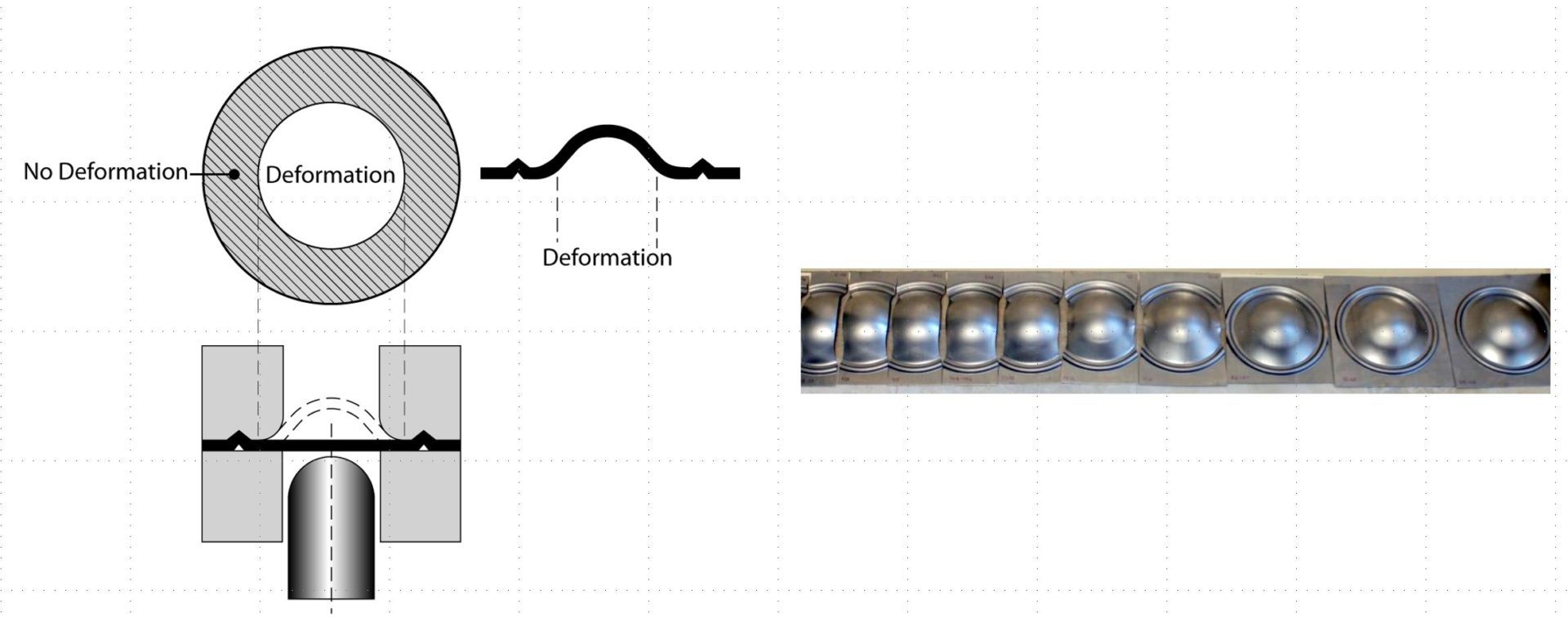
Figure 2: Forming limit curves can be created by deforming multiple samples of different widths. Narrow strips on the left allow metal to flow in from the unconstrained edges, creating a draw deformation mode leading to strains that plot on the left side of the FLC. Fully constrained samples, shown on the right^E-2, create a stretch deformation mode leading to strains that plot on the right side of the FLC.

Generally, strains are measured using one of two methods. The first approach involves covering the initially flat test samples with a grid pattern of circles, squares, or dots of known diameter and spacing to measure the strains associated with deformation. An alternate approach is based on Digital Image Correlation (DIC), where a camera tracks the movement of a random speckle pattern applied prior to forming.^W-26, ^H-22, ^M-21 DIC methods are directly suited for use with stress-based FLCs.

Differences between Forming Limit Curves

and Forming Limit Diagrams

Often, the terms Forming Limit Curve (FLC) and Forming Limit Diagram (FLD) are used interchangeably. Perhaps a better way of categorizing is to define the components and what they encompass. This is somewhat of a simplification, since detailed interactions are known to occur.

The Forming Limit Curve is a material parameter reflecting of the limiting strains resulting in necking failure as a function of strain path. It is a function of the metal grade, thickness, and sheet surface conditions, as well as the methods used during its creation (hemispherical/flat punch, test speed, temperature). It is applicable to any part shape.
Deforming a flat sheet into an engineered stamping results in a formed surface with strains as a function of the forming conditions like local radii, lubrication, friction, and of course part geometry. These strains are essentially independent of the chosen metal grade and thickness. Plotting these strains allows for a relative assessment of which strains are higher than others, but no judgment can be made on “how high is too high?”
The Forming Limit Diagram is a combination of the Forming Limit Curve (a material property) and the strains (reflecting part geometry and forming conditions). The FLD provides guidance on which areas of the formed part requires additional attention to achieve robust stamping conditions. Creating a subsequent FLD may be warranted when conditions change, since changes to the sheet metal properties (FLC) and the forming conditions (radii, lubrication, beads, blank size) will change the FLD, potentially affecting the conclusions.

Key Points

- Conventional Forming Limit Curves characterize necking failure only. Fractures at cut edges and tight bends may occur at strains lower than that suggested by the Forming Limit Curve.
- Differences in determination and interpretation of FLCs exist in different regions of the world.
- This system of FLCs commonly used for low strength and conventional HSLA is generally applicable to experimental FLCs obtained for DP steels for global formability.
- The left side of the FLC (negative minor strains) is in good agreement with experimental data for DP and TRIP steels. The left side depicts a constant thinning strain as a forming limit.
- Determination of FLCs for TRIP, MS, TWIP, and other special steels typically requires an experimental approach, since conventional simple equations do not accurately reflect the forming limits for these advanced microstructures.

Back to the Top

Generating Forming Limit Curves from Equations
Experimental Determination of Forming Limit Curves
Differences between Forming Limit Curves and Forming Limit Diagrams

Circle Grid Strain Analysis (CGSA)

Formability

A Forming Limit Curve (FLC) is a map of strains indicating the onset of critical through-thickness necking for different linear strain paths. The FLC is dependent on the metal grade and the specific methods used in its creation. When paired with the strains generated during forming of an engineered part, the associated Forming Limit Diagram (FLD) provides guidance on which areas of the part might be prone to necking failures during production stamping conditions that replicate those used in the analysis.

Several methods are available to measure the strains on formed parts. The earliest method is known as Circle Grid Strain Analysis (CGSA), with Dr. Stuart Keeler as its primary evangelist for nearly 50 years. Dr. Keeler was the Technical Editor of these AHSS Guidelines through Version 6.0, released in 2017.

As the name suggests, a flat blank is covered with a grid of circles of precisely known diameter, typically applied by electrochemical etching. Forming turns the circles into ellipses, with the dimensions related to the major and minor strains. Conventional measurement occurs after forming, and involves a calibrated Mylar™ strip marked with gradations indicating the expansion or contraction relative to the initial circle diameter. Typically, these are viewed through magnifiers, making it easier to discern the critical dimensional differences. Techniques and caveats are highlighted in Citations S-59 and S-60.

Instead of circles, most camera-based measurement techniques for analysis after forming use a regular grid pattern of squares or dots. Forming turns the squares into rectangles, and the camera/computer measures the expansion or contraction of the nodes at the corners of the squares to determine the strains. Similarly, forming changes the regular dot pattern, allowing for calculation of the strains.

These approaches determine only the strains after forming, and are constrained to assume linear strain paths. An alternate approach based on Digital Image Correlation (DIC), where a camera tracks the movement of a random speckle pattern applied prior to forming,^W-26, ^H-22, ^M-21 follows the strain evolution which occurs during forming and is not affected by non-linear strain paths.

Although DIC strain analysis is more accurate and informative, it is a higher-cost approach best suited for laboratory environments. Circle-grid, square-grid, and dot-grid strain analysis are all lower cost options and readily applied on the shop floor. Each of these in-plant techniques have different merits and challenges, including ease of use, accuracy, and cost.

N-Value

Mechanical Properties

N-Value, The Strain Hardening Exponent

Metals get stronger with deformation through a process known as strain hardening or work hardening, resulting in the characteristic parabolic shape of a stress-strain curve between the yield strength at the start of plastic deformation and the tensile strength.

Work hardening has both advantages and disadvantages. The additional work hardening in areas of greater deformation reduces the formation of localized strain gradients, shown in Figure 1.

Figure 1: Higher n-value reduces strain gradients, allowing for more complex stampings. Lower n-value concentrates strains, leading to early failure.

Consider a die design where deformation increased in one zone relative to the remainder of the stamping. Without work hardening, this deformation zone would become thinner as the metal stretches to create more surface area. This thinning increases the local surface stress to cause more thinning until the metal reaches its forming limit. With work hardening the reverse occurs. The metal becomes stronger in the higher deformation zone and reduces the tendency for localized thinning. The surface deformation becomes more uniformly distributed.

Although the yield strength, tensile strength, yield/tensile ratio and percent elongation are helpful when assessing sheet metal formability, for most steels it is the n-value along with steel thickness that determines the position of the forming limit curve (FLC) on the forming limit diagram (FLD). The n-value, therefore, is the mechanical property that one should always analyze when global formability concerns exist. That is also why the n-value is one of the key material related inputs used in virtual forming simulations.

Work hardening of sheet steels is commonly determined through the Holloman power law equation:

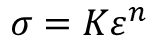
where
σ is the true flow stress (the strength at the current level of strain),
K is a constant known as the Strength Coefficient, defined as the true strength at a true strain of 1,
ε is the applied strain in true strain units, and
n is the work hardening exponent

Rearranging this equation with some knowledge of advanced algebra shows that n-value is mathematically defined as the slope of the true stress – true strain curve. This calculated slope – and therefore the n-value – is affected by the strain range over which it is calculated. Typically, the selected range starts at 10% elongation at the lower end to the lesser of uniform elongation or 20% elongation as the upper end. This approach works well when n-value does not change with deformation, which is the case with mild steels and conventional high strength steels.

Conversely, many Advanced High-Strength Steel (AHSS) grades have n-values that change as a function of applied strain. For example, Figure 2 compares the instantaneous n-value of DP 350/600 and TRIP 350/600 against a conventional HSLA350/450 grade. The DP steel has a higher n-value at lower strain levels, then drops to a range similar to the conventional HSLA grade after about 7% to 8% strain. The actual strain gradient on parts produced from these two steels will be different due to this initial higher work hardening rate of the dual phase steel: higher n-value minimizes strain localization.

Figure 2: Instantaneous n-values versus strain for DP 350/600, TRIP 350/600 and HSLA 350/450 steels.^K-1

As a result of this unique characteristic of certain AHSS grades with respect to n-value, many steel specifications for these grades have two n-value requirements: the conventional minimum n-value determined from 10% strain to the end of uniform elongation, and a second requirement of greater n-value determined using a 4% to 6% strain range.

Plots of n-value against strain define instantaneous n-values, and are helpful in characterizing the stretchability of these newer steels. Work hardening also plays an important role in determining the amount of total stretchability as measured by various deformation limits like Forming Limit Curves.

Higher n-value at lower strains is a characteristic of Dual Phase (DP) steels and TRIP steels. DP steels exhibit the greatest initial work hardening rate at strains below 8%. Whereas DP steels perform well under global formability conditions, TRIP steels offer additional advantages derived from a unique, multiphase microstructure that also adds retained austenite and bainite to the DP microstructure. During deformation, the retained austenite is transformed into martensite which increases strength through the TRIP effect. This transformation continues with additional deformation as long as there is sufficient retained austenite, allowing TRIP steel to maintain very high n-value of 0.23 to 0.25 throughout the entire deformation process (Figure 2). This characteristic allows for the forming of more complex geometries, potentially at reduced thickness achieving mass reduction. After the part is formed, additional retained austenite remaining in the microstructure can subsequently transform into martensite in the event of a crash, making TRIP steels a good candidate for parts in crush zones on a vehicle.

Necking failure is related to global formability limitations, where the n-value plays an important role in the amount of allowable deformation at failure. Mild steels and conventional higher strength steels, such as HSLA grades, have an n-value which stays relatively constant with deformation. The n-value is strongly related to the yield strength of the conventional steels (Figure 3).

Figure 3: Experimental relationship between n-value and engineering yield stress for a wide range of mild and conventional HSS types and grades.^K-2

N-value influences two specific modes of stretch forming:

Increasing n-value suppresses the highly localized deformation found in strain gradients (Figure 1).
A stress concentration created by character lines, embossments, or other small features can trigger a strain gradient. Usually formed in the plane strain mode, the major (peak) strain can climb rapidly as the thickness of the steel within the gradient becomes thinner. This peak strain can increase more rapidly than the general deformation in the stamping, causing failure early in the press stroke. Prior to failure, the gradient has increased sensitivity to variations in process inputs. The change in peak strains causes variations in elastic stresses, which can cause dimensional variations in the stamping. The corresponding thinning at the gradient site can reduce corrosion life, fatigue life, crash management and stiffness. As the gradient begins to form, low n-value metal within the gradient undergoes less work hardening, accelerating the peak strain growth within the gradient – leading to early failure. In contrast, higher n-values create greater work hardening, thereby keeping the peak strain low and well below the forming limits. This allows the stamping to reach completion.
The n-value determines the allowable biaxial stretch within the stamping as defined by the forming limit curve (FLC).
The traditional n-value measurements over the strain range of 10% – 20% would show no difference between the DP 350/600 and HSLA 350/450 steels in Figure 2. The approximately constant n-value plateau extending beyond the 10% strain range provides the terminal or high strain n-value of approximately 0.17. This terminal n-value is a significant input in determining the maximum allowable strain in stretching as defined by the forming limit curve. Experimental FLC curves (Figure 4) for the two steels show this overlap.

Figure 4: Experimentally determined Forming Limit Curves for mils steel, HSLA 350/450, and DP 350/600, each with a thickness of 1.2mm.^K-1

Whereas the terminal n-value for DP 350/600 and HSLA 350/450 are both around 0.17, the terminal n-value for TRIP 350/600 is approximately 0.23 – which is comparable to values for deep drawing steels (DDS). This is not to say that TRIP steels and DDS grades necessarily have similar Forming Limit Curves. The terminal n-value of TRIP grades depends strongly on the different chemistries and processing routes used by different steelmakers. In addition, the terminal n-value is a function of the strain history of the stamping that influences the transformation of retained austenite to martensite. Since different locations in a stamping follow different strain paths with varying amounts of deformation, the terminal n-value for TRIP steel could vary with both part design and location within the part. The modified microstructures of the AHSS allow different property relationships to tailor each steel type and grade to specific application needs.

Methods to calculate n-value are described in Citations A-43, I-14, J-13.