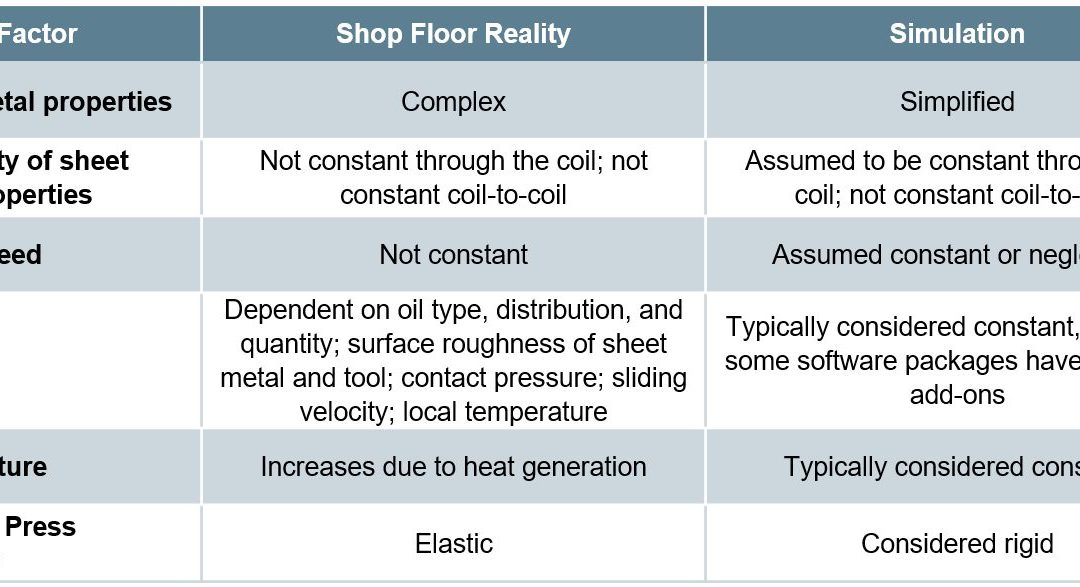
Simulation
Predicting metal flow and failure is the essence of sheet metal forming simulation. Characterizing the stress-strain response to metal flow requires a detailed understanding of when the sheet metal first starts to permanently deform (known as the yield criteria), how the metal strengthens with deformation (the hardening law), and the failure criteria (for example, the forming limit curve). Complicating matters is that each of these responses changes as three-dimensional metal flow occurs, and are functions of temperature and forming speed.
The ability to simulate these features reliably and accurately requires mathematical constitutive laws that are appropriate for the material and forming environments encountered. Advanced models typically improve prediction accuracy, at the cost of additional numerical computational time and the cost of experimental testing to determine the material constants. Minimizing these costs requires compromises, with some of these indicated in Table I created based on Citations B-16 and R-28.
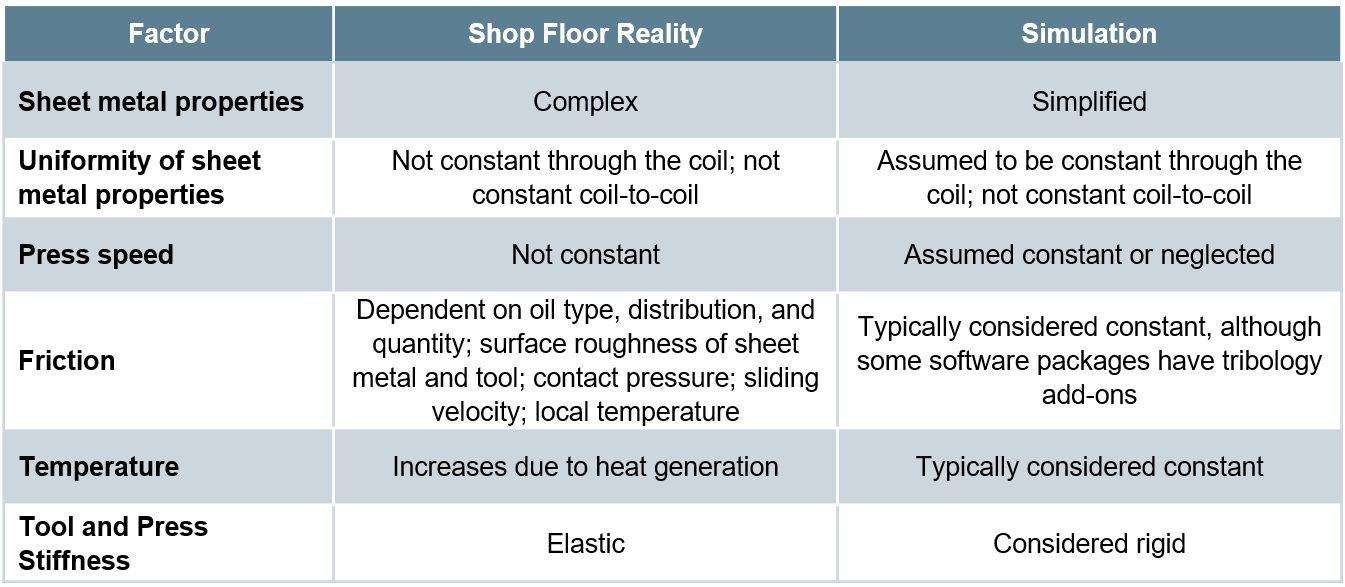
Table I: Deviations from reality made to reduce simulation costs. Based on Citations B-16 and R-28.
Yield Criteria
The yield criteria (also known as the yield surface or yield loci) defines the conditions representing the transition from elastic to plastic deformation. Assuming uniform metal properties in all directions allows for the use of isotropic yield functions like von Mises or Tresca. A more realistic approach considers anisotropic metal flow behavior, requiring the use of more complex yield functions like those associated with Hill, Barlat, Banabic, or Vegter.
No one yield function is best suited to characterize all metals. Some yield functions have many required inputs. For example, “Barlat 2004-18p” has 18 separate parameters leading to improved modeling accuracy – but only when inserting the correct values. Using generic textbook values is easier, but negates the value of the chosen model. However, determining these variables typically is costly and time-consuming, and requires the use of specialized test equipment.
Hardening Curve
Metals get stronger as they deform, which leads to the term work hardening. The flow stress at any given amount of plastic strain combines the yield strength and the strengthening from work hardening. In its simplest form, the stress-strain curve from a uniaxial tensile test shows the work hardening of the chosen sheet metal. This approach ignores many of the realities occurring during forming of engineered parts, including bi-directional deformation.
Among the simpler descriptions of flow stress are those from Hollomon, Swift, and Ludvik. More complex hardening laws are associated with Voce and Hockett-Sherby.
The strain path followed by the sheet metal influences the hardening. Approaches taken in the Yoshida-Uemori (YU) and the Homogeneous Anisotropic Hardening (HAH) models extend these hardening laws to account for Bauschinger Effect deformations (the bending-unbending associated with travel over beads, radii, and draw walls).
As with the yield criteria, accuracy improves when accounting for three-dimensional metal flow, temperature, and forming speed, and using experimentally determined input parameters for the metal in question rather than generic textbook values.
Failure Conditions
Defining the failure conditions is the other significant challenge in metal forming simulation. Conventional Forming Limit Curves describe necking failure under certain forming modes, and are easier to understand and apply than alternatives. Complexity and accuracy increase when accounting for non-linear strain paths using stress-based Forming Limit Curves. Necking failure is not the only type of failure mode encountered. Conventional FLCs cannot predict fracture on tight radii and cut edges, nor can they account for dimensional issues like springback. For these, failure criteria definitions which are more mathematically complex are appropriate.
Constitutive Laws and Their Influence
on Forming Simulation Accuracy
Many simulation packages allow for an easy selection of constitutive laws, typically through a drop-down menu listing all the built-in choices. This ease potentially translates into applying inappropriate selections unless the simulation analyst has a fundamental understanding of the options, the inputs, and the data generation procedures.
Some examples:
- The “Keeler Equation” for the estimation of FLC0 has many decades of evidence in being sufficiently accurate when applied to mild steels and conventional high strength steels. The simple inputs of n-value and thickness make this approach particularly attractive. However, there is ample evidence that using this approach with most advanced high strength steels cannot yield a satisfactory representation of the Forming Limit Curve.
- Even in cases where it is appropriate to use the Keeler Equation, a key input is the n-value or the strain hardening exponent. This value is calculated as the slope of the (natural logarithm of the true stress):(natural logarithm of the true strain curve). The strain range over which this calculation is made influences the generated n-value, which in turn impacts the calculated value for FLC0.
- The strain history as measured by the strain path at each location greatly influences the Forming Limit. However, this concept has not gained widespread understanding and use by simulation analysts.
- A common method to experimentally determine flow curves combines tensile testing results through uniform elongation with higher strain data obtained from biaxial bulge testing. Figure 1 shows a flow curve obtained in this manner for a bake hardenable steel with 220 MPa minimum yield strength. Shown in Figure 2 is a comparison of the stress-strain response from multiple hardening laws associated with this data, all generated from the same fitting strain range between yield and tensile strength. Data diverges after uniform elongation, leading to vastly different predictions. Note that the differences between models change depending on the metal grade and the input data, so it is not possible to say that one hardening law will always be more accurate than others.

Figure 1: Flow curves for a bake hardenable steel generated by combining tensile testing with bulge testing.L-20

Figure 2: The chosen hardening law leads to vastly different predictions of stress-strain responses.L-20
- Analysts often treat Poisson’s Ratio and the Elastic Modulus as constants. It is well known that the Bauschinger Effect leads to changes in the Elastic Modulus, and therefore impacts springback. However, there are also significant effects in both Poisson’s Ratio (Figure 3) and the Elastic Modulus (Figure 4) as a function of orientation relative to the rolling direction. Complicating matters is that this effect changes based on the selected metal grade.

Figure 3: Poisson’s Ratio as a Function of Orientation for Several Grades (Drawing Steel, DP 590, DP 980, DP 1180, and MS 1700) D-11

Figure 4: Modulus of Elasticity as a Function of Orientation for Several Grades (Drawing Steel, DP 590, DP 980, DP 1180, and MS 1700) D-11
Complete material card development requires results from many tests, each attempting to replicate one or more aspects of metal flow and failure. Certain models require data from only some of these tests, and no one model typically is best for all metals and forming conditions. Tests described below include:
- Tensile testing [room temperature at slow strain rates to elevated temperature with accelerated strain rates]
- Biaxial bulge testing
- Biaxial tensile testing
- Shear testing
- V-bending testing
- Tension-compression testing with cyclic loading
- Friction
Tensile testing is the easiest and most widely available mechanical property evaluation required to generate useful data for metal forming simulation. However, a tensile test provides a complete characterization of material flow only when the engineered part looks like a dogbone and all deformation resulted from pulling the sample in tension from the ends. That is obviously not realistic. Getting tensile test results in more than just the rolling direction helps, but generating those still involves pulling the sample in tension. Three-dimensional metal flow occurs, and the stress-strain response of the sheet metal changes accordingly.
The uniaxial tensile test generates a draw deformation strain state since the edges are free to contract. A plane strain tensile test requires using a modified sample geometry with an increased width and decreased gauge length,
Forming all steels involves a thermal component, either resulting from friction and deformation during “room temperature” forming or the intentional addition of heat such as used in press hardening. In either case, modeling the response to temperature requires data from tests occurring at the temperature of interest, at appropriate forming speeds. Thermo-mechanical simulators like Gleeble™ generate such data.
Conventional tensile testing occurs at deformation rates of 0.001/sec. Most production stamping occurs at 10,000x that amount, or 10/sec. Crash events can be 2 orders of magnitude faster, at about 1000/sec. The stress-strain response varies by both testing speed and grade. Therefore, accurate simulation models require data from higher-speed tensile testing. Typically, generating high speed tensile data involves drop towers or Split Hopkinson Pressure Bars.
A pure uniaxial stress state exists in a tensile test only until reaching uniform elongation and the beginning of necking. Extrapolating uniaxial tensile data beyond uniform elongation risks introducing inaccuracies in metal flow simulations. Biaxial bulge testing generates the data for yield curve extrapolation beyond uniform elongation. This stretch-forming process deforms the sheet sample into a dome shape using hydraulic pressure, typically exerted by water-based fluids. Citation I-12 describes a standard test procedure for biaxial bulge testing.
A Marciniak test used to create Forming Limit Curves generates in-plane biaxial strains. Whereas FLC generation uses 100 mm diameter samples, larger samples allow for extraction of full-size tensile bars. Although this approach generates samples containing biaxial strains, the extracted samples are tested uniaxially in the conventional manner.
Biaxial tensile testing allows for the determination of the yield locus and the biaxial anisotropy coefficient, which describes the slope of the yield surface at the equi-biaxial stress state. This test uses cruciform-shaped test pieces with parallel slits cut into each arm. Citation I-13 describes a standard test procedure for biaxial tensile testing. The biaxial anisotropy coefficient can also be determined using the disk compression testing as described in Citation T-21.
Shear testing characterizes the sheet metal in a shear loading condition. There is no consensus on the specimen type or testing method. However, the chosen testing set-up should avoid necking, buckling, and any influence of friction.
V-bending tests determine the strain to fracture under specific loading conditions. Achieving plane strain or plane stress loading requires use of a test sample with features promoting the targeted strain state.
Tension-compression testing characterizes the Bauschinger Effect. Multiple cycles of tension-compression loading captures cyclic hardening behavior and elastic modulus decay, both of which improve the accuracy of springback predictions. Again, no standard procedure exists. The biggest challenge with this test is preventing buckling from occurring during in-plane compressive loading. Related to this is the need to compensate for the friction caused by the anti-buckling mechanism in the stress-strain curves .
Friction is obviously a key factor in how metal flows. However, there is no one simple value of friction that applies to all surfaces, lubricants, and tooling profiles. The coefficient of friction not only varies from point to point on each stamping but changes during the forming process. Determining the coefficient of friction experimentally is a function of the testing approach used. The method by which analysts incorporate friction into simulations influences the accuracy and applicability of the results of the generated model.
Studies are underway to reduce the costs and challenges of obtaining much of this data. It may be possible, for example, to use Digital Image Correlation (DIC) during a simple uniaxial tensile testing to quantify r-value at high strains, determine the material hardening behavior along with strain rate sensitivity, assess the degradation of Young’s Modulus during unloading, and use the detection of the onset of local neck to help account for non-linear strain path effects.S-110
Application of Advanced Testing to Failure Predictions
Global formability failures occur when the forming strains exceed the necking forming limit throughout the entire thickness of the sheet. Advanced steels are at risk of local formability failures where the forming strains exceed the fracture forming limit at any portion of the thickness of the sheet.
Fracture forming limit curves plot higher than the conventional necking forming limit curves on a graph showing major strain on the vertical axis and minor strain on the horizontal axis. In conventional steels the gap between the fracture FLC and necking FLC is relatively large, so the part failure is almost always necking. The forming strains are not high enough to reach the fracture FLC.
In contrast, AHSS grades are characterized by a smaller gap between the necking FLC and the fracture FLC. Depending on the forming history, part geometry (tight radii), and blank processing (cut edge quality), forming strains may exceed the fracture FLC at an edge or bend before exceeding the necking FLC through-thickness. In this scenario, the part will fracture without signs of localized necking.
A multi-year study funded by the American Iron and Steel Institute at the University of Waterloo Forming and Crash Lab describes a methodology used for forming and fracture characterization of advanced high strength steels, the details of which can be found in Citations B-11, W-20, B-12, B-13, R-5, N-13 and G-19.
This collection of studies, as well as work coming out of these studies, show that relatively few tests sufficiently characterize forming and fracture of AHSS grades. These studies considered two 3rd Gen Steels, one with 980MPa tensile strength and one with 1180MPa tensile.
- The yield surface as generated with the Barlat YLD2000-2d yield surface (Figure 5) comes from:
- Conventional tensile testing at 0, 22.5, 45, 67.5, and 90 degrees to the rolling direction, determining the yield strength and the r-value;
- Disc compression tests according to the procedure in Citation T-21 to determine the biaxial R-value, rb.

Figure 5: Tensile testing and disc compression testing generate the Barlat YLD2000-2d yield surface in two 3rd Generation AHSS Grades B-13
- Creating the hardening curve uses a procedure detailed in Citations R-5 and N-13, and involves only conventional tensile and shear testing using the procedure included in Citation P-15.

Figure 6: Test geometries for hardening curve generation. Left image: Tensile; Right image: Shear.N-13
- Characterizing formability involved generating a Forming Limit Curve using Marciniak data or process-corrected Nakazima data. (See our article on non-linear strain paths) and Citation N-13 for explanation of process corrections]. Either approach resulted in acceptable characterizations.
- Fracture characterization uses four plane stress tests: shear, conical hole expansion, V-bending, and a biaxial dome test. The result from these tests calibrate the fracture locus describing the stress states at fracture.
Back To Top
![Correcting Springback]()
Springback
Overview
Forming a part at room temperature creates elastic stresses, which will require some form of springback correction to bring the stamping back to part print. Forming at sufficiently high temperatures, such as with press hardening steels, allows for stress relief before the part leaves the die.
Springback correction can take many forms. The first approach is to apply an additional process that changes the elastic stresses to a less damaging form. One example is a post-stretch operation that reduces sidewall curl by changing the tensile-to-compressive elastic stress gradient through the thickness of the sidewall to all tensile elastic stresses though the thickness. Another example is over-forming panels and channels so that the release of elastic stresses brings the part dimensions back to part print instead of becoming undersized.
A second approach is to modify the process and/or tooling to reduce the level of elastic stresses created during the forming operation. An example is to reduce sidewall curl by replacing sheet metal flowing through draw beads and over a die radius with a simple 90 degree bending operation.
A third approach for correcting springback problems is to modify product design to resist the release of the elastic stresses. Here, mechanical stiffeners added to the part design lock in the elastic stresses and maintain desired part shape.
The approaches to springback correction described below are applicable to all higher strength steels, and typically will address both angular change and sidewall curl. AHSS grades having high flow stress in the formed part may require one or more of these approaches for satisfactory dimensional accuracy.
Minimizing springback through compensation in the first draw stage is more effective and less expensive than attempting to correct for existing springback in subsequent re-strike or re-forming operations. Approaches for improved dimensional accuracy include:
- Minimizing bending/unbending as the metal flows to the final part shape reduces distortion and tool wear.
- Reaching minimum strain levels across the panel minimizes springback and sidewall curl.
- Accounting for tool material loss during recuts helps ensure sufficient tool stiffness to counteract the higher press forces required with AHSS grades.
- Keeping the depth of AHSS channel-shaped parts as uniform as possible avoids forming distortions. Gradual shape transitions will minimize distortions, especially in areas of metal compression. Designing radii so there are only gradual transitions avoids stress risers and minimizes distortions. Minimize stretch/compression flanges wherever possible.
- If die and process design cannot relieve all elastic stresses, then creating a uniformly distributed residual stress pattern across the sheet and through the thickness will help eliminate the source of mechanical multiplier effects and thus lead to reduced springback problems.
Correcting Springback by Changing the Elastic Stress Distribution: Post-Stretch (Stake Beads, Hybrid Beads, and Active Binder Force Control)
One of the most effective techniques for significant reduction of both angular change and sidewall curl is a post-stretch operation. Applying an in-plane tensile force after all operations in which the sheet metal is bent and unbend over draw beads and across die radii can change the through-thickness tensile-to-compressive elastic stress gradients to all tensile elastic stresses.
When the part is still in the die, the outer surface of the bend over the punch radius is in tension (Point A in Figure 1), while at the same time the inner surface is in compression (B). After the punch retracts and the part is no longer under load, the tensile elastic stresses (A) tend to shrink the outer layers and the compressive elastic forces (B) tend to elongate the inner layers. These opposite forces form a mechanical advantage to magnify the angular change. The differential stress ∆σ is the driver for the dimensional change. Note that this reversal in stress direction after removal of the applied load is the same root cause that results in snap-through reverse tonnage reactions when punching higher strength steels.

Figure 1: Sheet metal bent over a punch radius has elastic stresses of the opposite sign creating a mechanical advantage to magnify angular change. Similar effects create sidewall curl for sheet metal pulled through draw beads and over die radii. When the part is no longer under load, it will change shape to relieve these elastic stresses.
In the case of side wall curl, this differential stress ∆σ increases as the sheet metal is work hardened going through draw beads and around the die radius into the wall of the part.
To correct this angular change and sidewall curl, apply a tensile stress to the flange end of the wall to generate a minimum tensile strain of 2% within the sidewall of the stamping. Figure 2 describes the sequence of events. The initial elastic states are tensile (A1) and compressive (B1). When approximately 2% tensile strain is added to A1, the strain point work hardens and moves up slightly to A2. However, when 2% tensile strain is added to B1, the compressive elastic stress state first decreases to zero, then climbs to a positive level and work hardens slightly to point B2. The neutral axis is moved out of the sheet metal. The stress differential ∆σ now approaches zero. Instead of bending or curving outward, the wall simply shortens by a small amount similar to releasing the load on a tensile test sample. This shortening of the wall length can be easily corrected by an increased punch stroke.

Figure 2: The large stress differential shown in Figure 1 is significantly reduced by applying a 2% tensile strain.
Post-Stretch with Stake Beads
Two die design methods currently in use can create the desired minimum 2% post-stretch on the sidewall of AHSS parts, both of which utilize what are commonly referred to as stake beads.
The first method involves retractable beads located in machined slots in the lower blankholder. The upper blankholder has machined stake bead pockets. Adjustable stop blocks located directly under the retractable stake beads can be shimmed to alter the timing when the stake bead engages the stamping, if required.
At the targeted punch stroke position, the retractable beads hit the stop blocks which forces them into the sheet metal flange. This creates a blank locking action while the punch continues to deform the part. As the die opens, the stake beads retract, and the cycle repeats itself from press stroke to press stroke. Adjustability of the draw bead height has advantages, particularly during initial die tryout.
As the retractable beads are inserts, removing them for hardening, coating, polishing, etc., is much easier than moving an entire die to perform bead work. Duplicate inserts can also be made, even utilizing alternative tool steels to increase durability. Locating the retractable stake bead on the blankholder, however, can lead to a larger required blank size. Die construction costs for retractable stake beads are also higher due to the additional machining required.
It is important to have adequate structural die support to avoid breaking the die. Significantly greater lateral thrust forces can cause catastrophic die failure if the stake beads are located too close to the punch opening. This is also true for many other die components, so die construction standards for mild and HSLA steels may not apply to AHSS.
An alternate approach is to locate the stake beads on the punch. Stake beads are machined directly in the punch casting, with the stake bead pockets machined into the upper die cavity. This approach may allow for a reduced blank size, since less material is needed outside the punch opening to accommodate both the draw bead and the stake bead. Figure 3 shows a DP590 B-pillar draw panel with draw beads located on the blankholder and stake beads located on the punch just inboard of the draw beads.

Figure 3: DP590 B-pillar with draw beads on the blankholder and stake beads on the punch. Yellow arrows point to the stake beads; blue arrows point to the draw beads located closer to the edge of the draw panel.
Figure 4 shows a draw die punch with stake beads machined at the very edge of the punch opening, along with the upper die with the stake bead pockets machined out.

Figure 4: Left Image – Stake beads machined into the punch of this DP780 die; Right Image: Stake bead pockets machined into the upper draw die. Note that there are no draw beads on this blankholder.
Draw beads control metal flow in draw dies. However, draw beads may become less functional when forming higher strength sheet steels having higher work hardening characteristics. Here, bending and straightening when pulling the sheet through the punch opening radius, combined with bearing on the binder surface, may be sufficient to control metal flow.
The punch and upper binder in Figure 4 have no draw beads, and instead exhibit stake beads that engage late in the press stroke. This solution is lower in cost but provides limited flexibility since the beads are machined directly into the die. In contrast, Figure 5 shows a die with removable stake bead inserts located on the punch. This approach has improved adjustability, but the added expense of machining the die and installing stake bead inserts.

Figure 5: This die has adjustable stake beads located on the punch as inserts, and do not retract during every press stroke. Note also that there are no draw beads on the blankholder.A-6
A third option to achieve the post forming 2% strain on the part with stake beads involves an additional die or die station. After nearly fully forming the part in the first die, a second die locks the remaining flange in place and further deforms the part by the additional 2%. This approach is expensive since it requires construction of an additional die, or if processed in a progressive die, adding this extra station increases the size and complexity of the progressive die.
Ensuring dimensional precision may require a restrike operation after trimming. In addition to sharpening the radii, the restrike die may provide the sidewall stretch (post-stretch) of approximately 2% required to eliminate curl.
Studies have shown that the height and geometry of the stake bead can impact springback control. Insufficient stretching below the targeted 2% post-stretch may not sufficiently address springback. If the restraining force of the stake bead is too great, it could lead to fracture at the bead or punch opening radius.
Adjusting the stake bead geometry around the part creates an unbalanced post-stretching configuration. Researchers applied this approach to counteract springback in a 3rd Generation steel, with more shallow beads used on deeper drawn sections of the tested part.J-11
The magnitude of springback is a function of the uniformity of the stress distribution through the thickness direction the wall of the formed sheet. An optimized combination of draw beads and stake beads promotes a uniform stress distribution through the thickness, which leads to improved springback control (Figures 6 and 9). Successful simulation provides a range of acceptable combinations of draw bead and stake bead heights.Z-15

Figure 6: A combination of draw beads and stake beads promote a uniform stress distribution through the thickness, leading to improved springback control.Z-15
Press Force and Energy Considerations when using Stake Beads
These post-stretch forming operations normally require significantly higher forming forces and energy requirements to be effective for several reasons.
Any sheet metal will work harden after going through draw beads. Since AHSS grades work harden to a greater degree than conventional high strength steels, the AHSS grades have significantly higher yield strength once the blank has passed over the draw beads. As stake beads are located inboard of draw beads, the stake bead must now deform material with a much higher yield strength due to the work hardening created by the bending and straightening of the material from being pulled through the draw bead.
Since stake beads engage late in the press stroke, their use has similar implications as creating embossments as discussed in a Press Energy case study in the Press Requirements page. This Case StudyH-3 shows that the last increment of punch travel required to finish embossing requires significantly higher energy for AHSS versus conventional mild or HSLA steel. In the current discussion on stake beads, inducing an additional 2% post forming strain into the part will also require higher forming forces and energy requirements, since the forming process work hardened and strengthened the sidewalls. Even if the press has sufficient force and energy characteristics, avoid necking down and tearing the sheet metal as it bends over the punch radius.
Case Studies: Using Stake Beads to Reduce Springback L-1
This case study evaluated springback on specially constructed dies tested using several grades of conventional and advanced high strength steels, including HSLA, dual phase, and TRIP grades with tensile strength ranging from 450 MPa to 980 MPa. One die used the conventional approach, allowing for metal to flow from the flange without a bead. The second die had a recessed square stake bead in the flange that created a post-stretch condition near the end of the stroke. As expected, the post-stretch die resulted in dramatically lower springback (Figure 7). In addition, springback on parts made with this die was not a function of the sheet metal tensile strength, making for a more robust process.

Figure 7: Comparison of two DP 450/750 parts, where stake beads in the bottom part minimized springback. Both images are different angles of the same parts.L-1
Post-Stretch with Hybrid Beads
As seen in the prior figures, the stake beads geometry plays an important role in restricting the metal flow when stretching the sidewalls during the last stages of the punch stroke. This approach requires a larger blank to accommodate the bead, and must be used in a press with sufficient tonnage to set the bead.
A modified approach significantly reduces the blank size requirements as well as lowers the required tonnages to create the bead. It uses stinger beads to penetrate the sheet metal as well as create a wave shape in the deformed region which restricts metal flow. This so-called hybrid bead takes up less than 25% of the bead surface area compared with a conventional stake bead, allowing for a measurably smaller blank. There is no bending over tight bead radii, eliminating the splitting risk at the bead. The restricted metal motion across the beads further minimizes the stress differential between the two sheet steel surfaces, which eliminates a significant root cause of sidewall curl.
Figure 8 highlights the influence a hybrid bead has on springback of a 3rd Generation Steel having a minimum tensile strength of 980MPa.

Figure 8: Hybrid bead dramatically reduces springback in a 3rd Generation steel having 980 MPa minimum tensile strength, while taking up less space and requiring reduced tonnage than stake beads.A-6
Animations of the process sequence is presented in Figures 9 and 10, with more information available in Citations J-12 and W-19.

Figure 9: Animation showing a combination of draw beads and stake beads to reduce springback.A-6
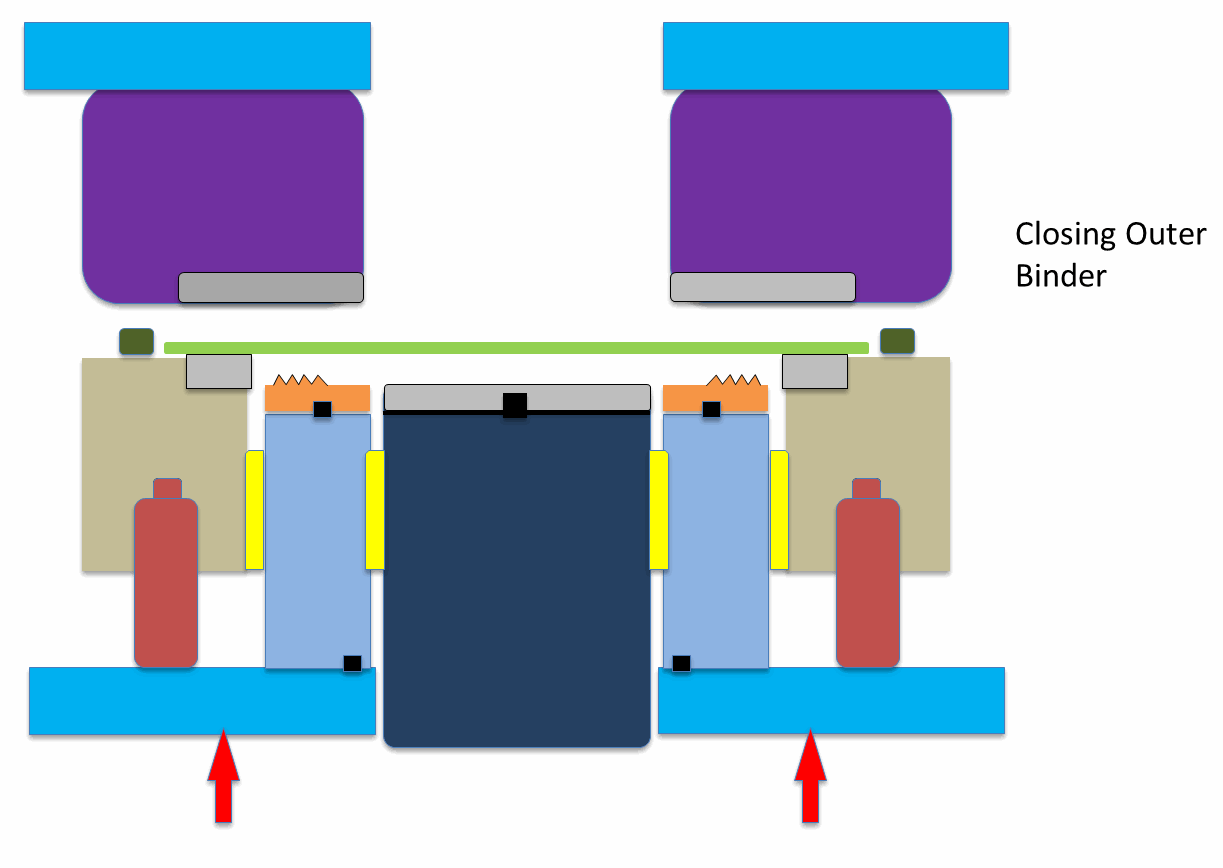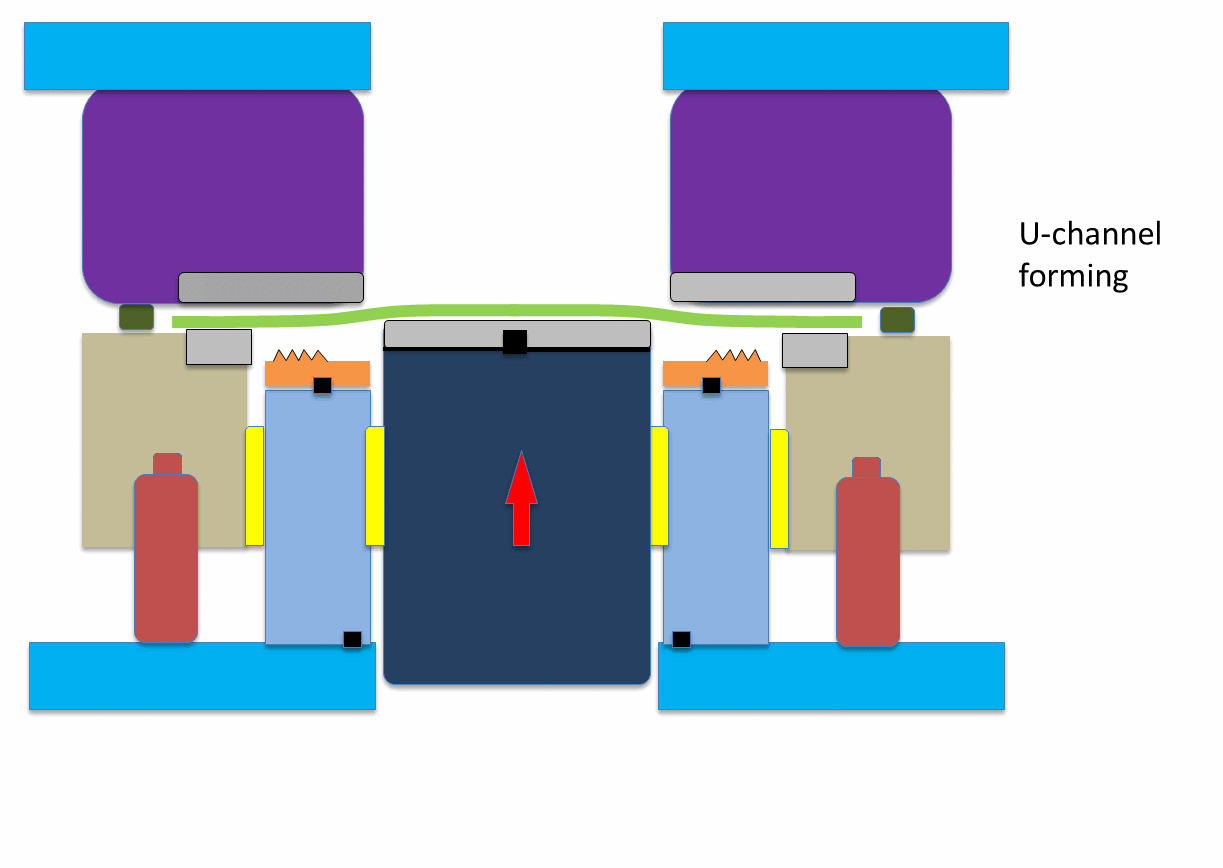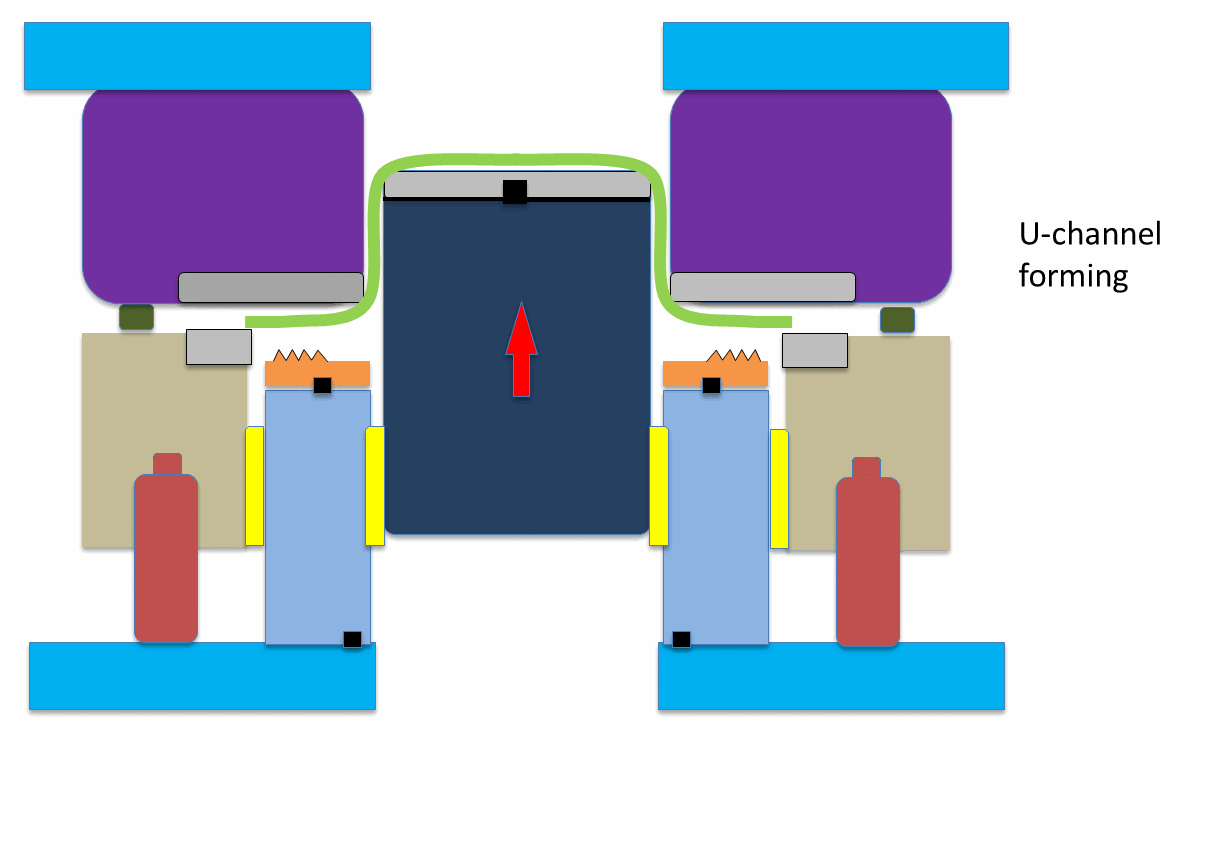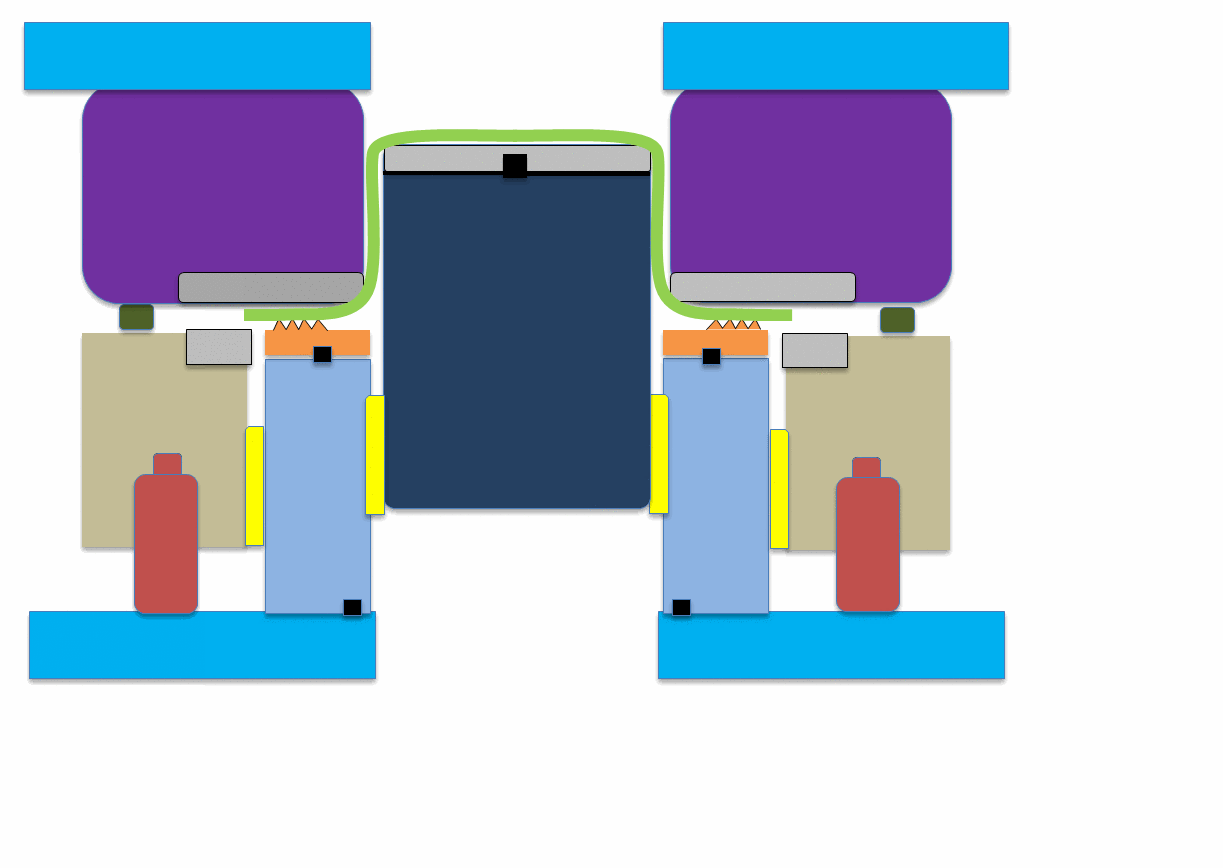
Figure 10: Animation showing application of hybrid beads to reduce springback.A-6
Post-Stretch with Active Binder Force Control
While most stamping processes apply binder pressure uniformly throughout the press stroke, modern stamping presses can be equipped with cushions having multipoint-control systems. Adjusting the associated pressure profile around the panel and throughout the stroke optimizes metal flow, prevent splits and wrinkles, and minimize thinning. This active binder force control capability allows for application of increased blank holder force at any point of the stroke, including at the end to achieve the targeted 2% post-stretch needed to minimize springback. (See the AHSS Insights blog by Dr. Daniel Schaeffler from Engineering Quality Solutions, Inc.)
Beyond simply increasing the blank holder force at the end of the stroke, varying the pressure sequence during the stroke may be beneficial as well. DP 340/590 steel was stamped using a constant binder force, an increasing binder force starting low and finishing high, and a third approach where the initial part of the stroke formed the part with a medium binder force which dropped for most of the stroke but increased at the end to apply the sidewall tension. This third approach resulted in the least angular change and sidewall curl, as seen in Figure 11.

Figure 11: DP 340/590 stamped with constant binder force (top), low-to-high binder force (middle), and medium-to-low-to-high binder force (bottom).P-14
Many angular change problems initiate when constructing the tooling either to part print or without sufficient springback compensation. Achieving targeted dimensions may require over-forming or over-bending.
Use rotary bending tooling where possible instead of flange wipe dies. Rotary bending allows for easy adjustment of the bending angle to correct for changes in springback due to variations in steel properties, die set, lubrication, and other process parameters. In addition, the tensile loading generated by the wiping shoe is absent.
However, if over-bending with flange wipe dies is the chosen approach to minimize angular change, use die radii less than the part radius and use back relief for the die and punch (Figure 12). This approach intentionally subjects the bending radius to compressive stresses between the punch and die. The squeezing and associated thinning at the bend radius results in plastic deformation of the sheet steel, with little elastic recovery after unloading from the press.

Figure 12: Providing back relief on the flange steel and lower die aids over-bending.A-2
Cross section design for longitudinal rails, pillars, and cross members impacts the effectiveness of springback compensation methods. The rail cross section in sketch A of Figure 13 does not allow the use of over-bending for springback compensation in the forming die. In addition, this design likely leads to severe sidewall curl in AHSS channel-shaped cross sections. Minimize these quality issues by designing a cross section that allows for over-bending during forming, as shown in sketch B. Reduced sidewall curl is another benefit of this cross-sectional design. Springback allowance must increase as strength increases. Typical wall opening angles are 3-degrees for Mild steel, 6 degrees for DP 350/600 and 10 degrees for DP 850/1000 or TRIP 450/800. In addition, the cross section in sketch B will have the effect of reducing the impact shock load when the draw punch contacts the AHSS sheet. The vertical draw walls shown in sketch A require higher binder pressures and higher punch forces to maintain process control.

Figure 13: Changing a rail cross section from A to B allows easier over-bending for springback control.N-3
Producing closed box sections involves welding two channel sections together at their flanges. Hat-sections with 90-degree corners such as seen in sketch A of Figure 14 will experience many production problems since each component will have issues with sidewall curl and angular change. The hexagonal section in sketch B will reduce sidewall curl and twist problems, while permitting over-bend for springback compensation in the stamping dies.

Figure 14: Changing the design of a closed cross section from A to B leads to a reduction in springback problems.N-3
Adding extra stages to the forming process allows for secondary operations to return a sprung part back to nominal dimensions. For example, Figure 15 shows a process where a crown existing in the first step when forming a channel section uses a second die for flattening and eliminating sidewall springback.

Figure 15: Schematic showing how flattening a crown corrects angular springback.A-3
As a related process, multiple stage forming (Figure 16) is an option to minimize springback and improve dimensional accuracy when stamping rails or other parts with a hat-shaped cross section consisting of right angles. This processing approach creates a design which avoids re-working previously-formed (and therefore work hardened) sections.
In the first operation, all 90-degree radii and mating surfaces are formed using “gull-wing” processes with over bending to compensate for springback. The larger radius in the top of the hat section gets flattened in the second stage. Certain cases may require an over bending of the flat top section.
Multiple-stage forming also helps when forming parts having small geometrical features of severe geometry that can be formed only in the re-strike operation. A part that has a variable cross section in combination with small geometrical features may need a coining operation in the second or last stage of the forming process. This may be the only way to control the geometry.

Figure 16: Two-stage forming produces a dimensionally accurate hat section with relatively small radii.R-1
Correcting Springback by Reducing or Minimizing the Elastic Stresses
The process design, and therefore the tooling design, can drastically affect the level of the elastic stresses in the part.
As an example, different blankholder actions provide four possible processes to form a hat-profile channel, each with different dimensional accuracy (Figure 17). The four processes are:
- Draw: the conventional forming type with continuous blankholder force and all blank material undergoing maximum bending and unbending over the die radius. This forming mode creates maximum sidewall curl.
- Form-draw: a forming process in which application of the blank holder force occurs between the middle and last stage of forming. It is most effective to reduce the sidewall curl because this approach minimizes bend unbend deformation at the beginning of the stroke prior to application of any blank holder force. Applying a large tensile stress during the last stage of forming creates the post-stretch condition to further minimize curl.
- Form: a process where the flange is created during in the last stage of forming and the material undergoes only a slight amount of bend-unbend deformation. Depending on the part geometry, the lack of a blankholder may lead to wrinkles.
- Bend is a simple bending process to reduce the sidewall curl, which avoids the bend and unbend sequence associated with sidewall curl. However, this approach likely leads to an angular change in the sidewall.

Figure 17: Four processes for generating a channel for bumper reinforcement create different levels of elastic stress and springback.K-5
Correcting Springback by Locking in the Elastic Stresses
Where part design allows, geometrical features like darts, beads, and stiffeners prevent the release of the elastic stresses and reduce various forms of springback. Minimize twist by adding strategically placed vertical beads, darts, or other geometric stiffeners in the shorter length wall to equalize the length of line.
Applying these features in a restrike operation may not be possible due to equipment or design limitations, since the yield strength of the sheet metal increases after work hardening. In the case of AHSS grades, this work hardening leads to a dramatic increase in strength.
Any elastic stress locked into the panel remains in the part as residual or trapped stresses. Subsequent forming, trimming, punching, heating, or other processes may unbalance the residual stress and change the part shape. For these reasons, the full process needs to be simulated, incorporating both material and geometrical changes occurring in all prior operations.
Figures 18 to 22 present examples of how elastic stresses can be locked into the part to control for springback.

Figure 18: Geometrical stiffeners like flanges or beads lock elastic stresses into the part, fixing the part shape.A-2

Figure 19: B-pillar using stiffening darts to control springback.A-41

Figure 20: Step flange locks in elastic stresses on a draw wall.A-41

Figure 21: Hat section showing the effects geometrical features have on controlling springback. Angular change and sidewall curl are noticeably less pronounced on the left side having the vertical beads, compared with the right side where no springback mitigation methods were employed.K-14

Figure 22: DP600 front rail upper reinforcement with vertical beads designed into the part geometry for springback control.F-9
An American Iron and Steel Institute study defined several tool and process parameters that reduced angular change and side wall curl (Figures 23 and 24). As expected, angular change and curl increase with yield strength. Tighter clearances, smaller punch radii, and higher drawbead restraining forces reduced both types of springback.S-47

Figure 23: The effect of tool parameters in angular change. The lower values are better.S-47

Figure 24: The effect of tool parameters in sidewall curl. Higher values of radius of curl are better.S-47
Figure 25 highlights the importance of keeping the die clearance as tight as allowed by formability and press capability. Unwanted bending and unbending work hardens the sheet metal and promotes increases in springback.

Figure 25: Reducing die clearance restricts additional bending and unbending as the sheet metal comes off the die radius, minimizing angular change.Y-2
Figure 26 illustrates that angular change increases dramatically for higher strength steels as the bend radius increases. Minimizing angular change requires designing the punch radius as sharp as formability and product/style allows. However, with AHSS grades, sharp radii may promote the local formability failure mode of shear fracture. Inside product feature radii should be a minimum of 3T for any AHSS grade having a tensile strength at or above 590 MPa. Die radii at draw beads, punch openings, etc., where the material is pulled under tension over a radius should be at least 5T for any AHSS grade over 590 MPa. Minimum bend radii requirements may be even greater as strength levels continue to increase, roll forming excluded. To avoid problems due to specifying the wrong AHSS grade for the wrong application, bend testing and hole expansion testing should be used in conjunction with close communication with the steel supplier when selecting the proper die radius for the intended AHSS material. In addition, sharp radii contribute to excessive thinning at the tangent to the radius when global formability failures are of concern.

Figure 26: Angular change increases with yield strength and bend radius at a constant thickness.S-2
Case Study in Springback Reduction Strategies
Automakers face conflicting constraints of lightweighting while improving safety performance. The B-Pillar Inner plays a significant role in meeting ever-increasing roof crush and side impact performance requirements. A studyM-17 published in 2007 showed the tooling and design changes made when transitioning from HSLA 340/440 to DP 550/980. These changes, shown in Figure 27, include adding sidewall beads to control springback, along with geometry to improve section stiffness.

Figure 27: Strategies to reduce springback in a DP 550/980 B-Pillar Inner.M-17
Another approach is highlighted in a Webinar from 2020.S-105 When forming hat-shaped sections, sidewall curl is minimized by using a cam to form the sidewall-flange area, followed by a more conventional sidewall stretch at the end (Figure 28). The animation in Figure 29 shows the process.S-6

Figure 28: Cam bending of sidewall-flange area minimizes springback.S-105
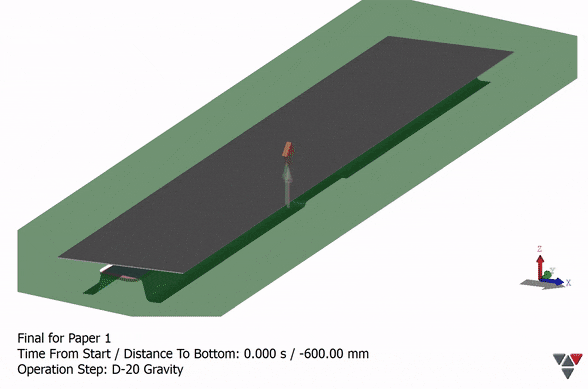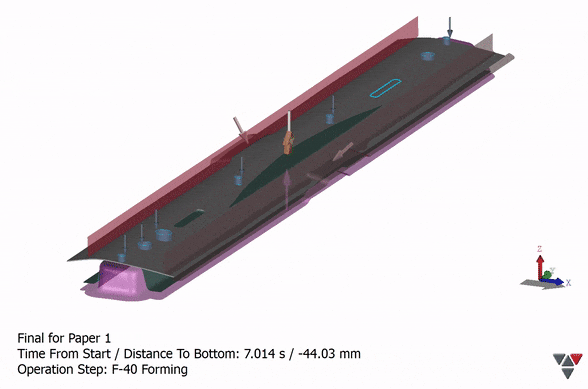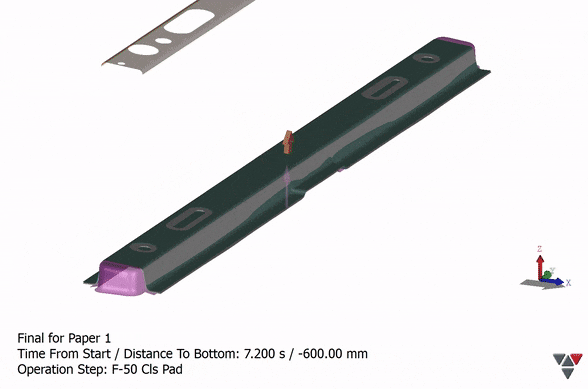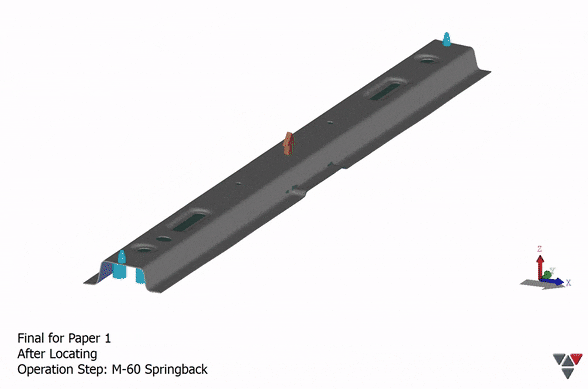
Figure 29: Animation of hat-section forming process to minimize springback.S-6
Compressive Stress Superposition for Springback Reduction
As explained above, springback and curl initiate when there are tensile stresses on one surface and compressive stresses on the other surface of the sheet. One of the keys to springback reduction is balancing these stresses through the sheet thickness.
A patented process known commercially as Smartform® relies on compressive stress superposition to achieve this stress balance. B-76 , L-65, B-77,, V-23
Achieving compressive stress superposition uses a two-step process where in the first preform step, the blank is formed into a “U” shape having a similar contour to the finished component, and then a sizing step to adjust the dimensional accuracy. This second step compresses the sheet metal during sizing rather than making it thinner from a drawing operation.
In the preforming stage (OP20), geometrical flexibility in the design of the tool surface exists, as the final component contour is not set until the sizing calibration stage (OP30). This allows for enlarged radii and wall angles to be used as countermeasures to prevent wrinkling and cracks.
Since the preform is not drawn, the starting blank can be cut to almost the same size as its final geometry before it is formed, reducing the number of trimming operations in the die process, as well as the amount of material used. Reportedly, an average of 15 percent materials savings occurs relative to conventional types of forming, with the actual savings being dependent on the size and complexity of the component.
Another benefit: resulting from the way the stress balance is achieved, this technology is relatively insensitive to variations in sheet metal properties, leading to a highly robust process.
Compressive stress superposition has been shown to work for steels having minimum specified tensile strength of 590 MPa through 1180 MPa.
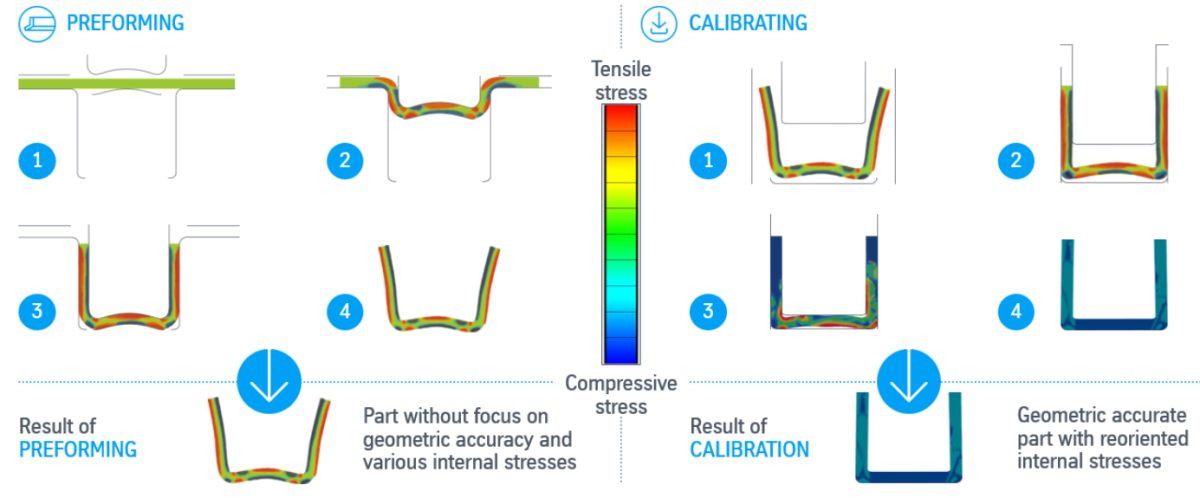
Figure 30: Compressive Stress Superposition Stress Conditions. Left: Preforming (OP20). Right: Sizing and Calibration (OP30). L-65
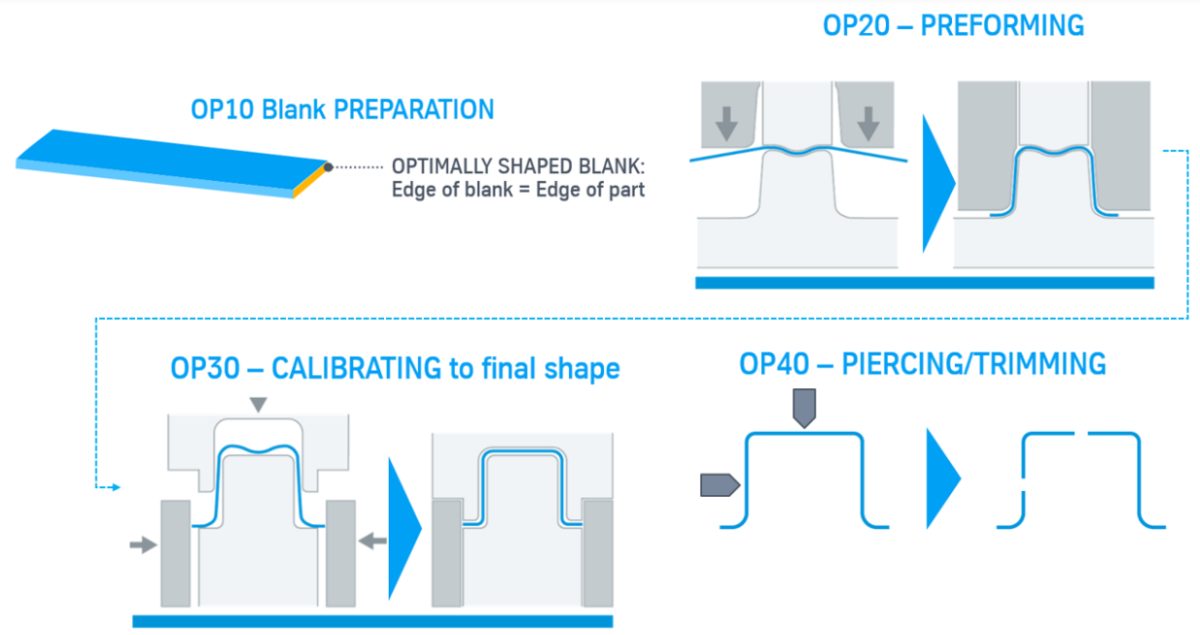
Figure 31: Compressive Stress Superposition Die Process.L-65
Key Points
Several process and design modifications remove (or at least minimize and stabilize) the different modes of springback found in channels and similar configurations:
- Open wall angles achieved with minimized metal flow over die radii minimize angular change and sidewall curl.
- Overbending accounts for angular change, allowing the part to spring back to the targeted dimensions. Subjecting the bending radius to compressive stresses at the bottom of the press stroke plastically deforms the sheet metal, minimizing the elastic stresses associated with springback. Note that this approach is less successful in addressing sidewall curl.
- Applying in-plane tension to the side walls after forming reduces springback. Methods include using stake-beads, hybrid beads, or active binder force control. However, with higher strength steels, it may be difficult to achieve sufficient stretch to the sidewall by simply increasing the blank holding force. Preventing metal flow into the wall during post-stretching may require lock beads. Bead geometry affects blank size and press requirements.
- Geometric stiffeners like darts, beads, and flanges lock elastic stresses in place preventing springback from occurring. Subsequent forming or trimming operations may relieve these stresses, resulting in dimensional distortion. In addition, the selected press must have the load and energy requirements to form these features.
Design the part and tool in such a way that springback is desensitized to variations in material, gauge, tools and forming processes (a robust system and process) and that the effects of springback are minimized rather than attempt to compensate for it.
The accuracy of forming simulation programs to predict springback continues to improve, especially if it incorporates a complete material characterization and the chosen model is appropriate for the challenges of the specific part and forming method. Even without full accuracy, springback simulations can predict the trend and test the effectiveness of proposed countermeasures. In all cases, verify predictions against physical measurements.
Back To Top
![Correcting Springback]()
Mechanical Properties
Elastic Modulus (Young’s Modulus)
When a punch initially contacts a sheet metal blank, the forces produced move the sheet metal atoms away from their neutral state and the blank begins to deform. At the atomic level, these forces are called elastic stresses and the deformation is called elastic strain. Forces within the atomic cell are extremely strong: high values of elastic stress results in only small magnitudes of elastic strain. If the force is removed while causing only elastic strain, atoms return to their original lattice position, with no permanent or plastic deformation. The stresses and strains are now at zero.
A stress-strain curve plots stress on the vertical axis, while strain is shown on the horizontal axis (see Figure 2 in Mechanical Properties). At the beginning of this curve, all metals have a characteristic linear relationship between stress and strain. In this linear region, the slope of elastic stress plotted against elastic strain is called the Elastic Modulus or Young’s Modulus or the Modulus of Elasticity, and is typically abbreviated as E. There is a proportional relationship between stress and strain in this section of the stress-strain curve; the strain becomes non-proportional with the onset of plastic (permanent) deformation (see Figure 1).

Figure 1: The Elastic Modulus is the Slope of the Stress-Strain Curve before plastic deformation begins.
The slope of the modulus line depends on the atomic structure of the metal. Most steels have an atomic unit cell of nine iron atoms – one on each corner of the cube and one in the center of the cube. This is described as a Body Centered Cubic (BCC) structure. The common value for the slope of steel is 210 GPa (30 million psi). In contrast, aluminum and many other non-ferrous metals have 14 atoms as part of the atomic unit cell – one on each corner of the cube and one on each face of the cube. This is referred to as a Face Centered Cubic (FCC) atomic structure. Many aluminum alloys have an elastic modulus of approximately 70 GPa (10 million psi).
Under full press load at bottom dead center, the deformed panel shape is the result of the combination of elastic stress and strain and plastic stress and strain. Removing the forming forces allows the elastic stress and strain to return to zero. The permanent deformation of the sheet metal blank is the formed part coming out of the press, with the release of the elastic stress and strain being the root cause of the detrimental shape phenomenon known as springback. Minimizing or eliminating springback is critical to achieve consistent stamping shape and dimensions.
Depending on panel and process design, some elastic stresses may not be eliminated when the draw panel is removed from the draw press. The elastic stress remaining in the stamping is called residual stress or trapped stress. Any additional change to the stamped panel condition (like trimming, hole punching, bracket welding, reshaping, or other plastic deformation) may change the amount and distribution of residual stresses and therefore potentially change the stamping shape and dimensions.
The amount of springback is inversely proportional to the modulus of elasticity. Therefore, for the same yield stress, steel with three times the modulus of aluminum will have one-third the amount of springback.
Elastic Modulus Variation and Degradation
Analysts often treat the Elastic Modulus as a constant. However, Elastic Modulus varies as a function of orientation relative to the rolling direction (Figure 2). Complicating matters is that this effect changes based on the selected metal grade.

Figure 2: Modulus of Elasticity as a Function of Orientation for Several Grades (Drawing Steel, DP 590, DP 980, DP 1180, and MS 1700) D-11
It is well known that the Bauschinger Effect leads to changes in the Elastic Modulus, and therefore impacts springback. Elastic Modulus determined in the loading portion of the stress-strain curve differs from that determined in the unloading portion. In addition, increasing prestrain lowers the Elastic Modulus, with significant implications for forming and springback simulation accuracy. In DP780, 11% strain resulted in a 28% decrease in the Elastic Modulus, as shown in Figure 3.K-7

Figure 3: Variation of the loading and unloading apparent modulus with strain for DP780K-7
Another study documented the modulus degradation for many steel grades, including mild steel, conventional high strength steels, and several AHSS products.W-10 Data in some of the grades is limited to small plastic strains, since valid data can be obtained from uniaxial tensile testing only through uniform elongation.
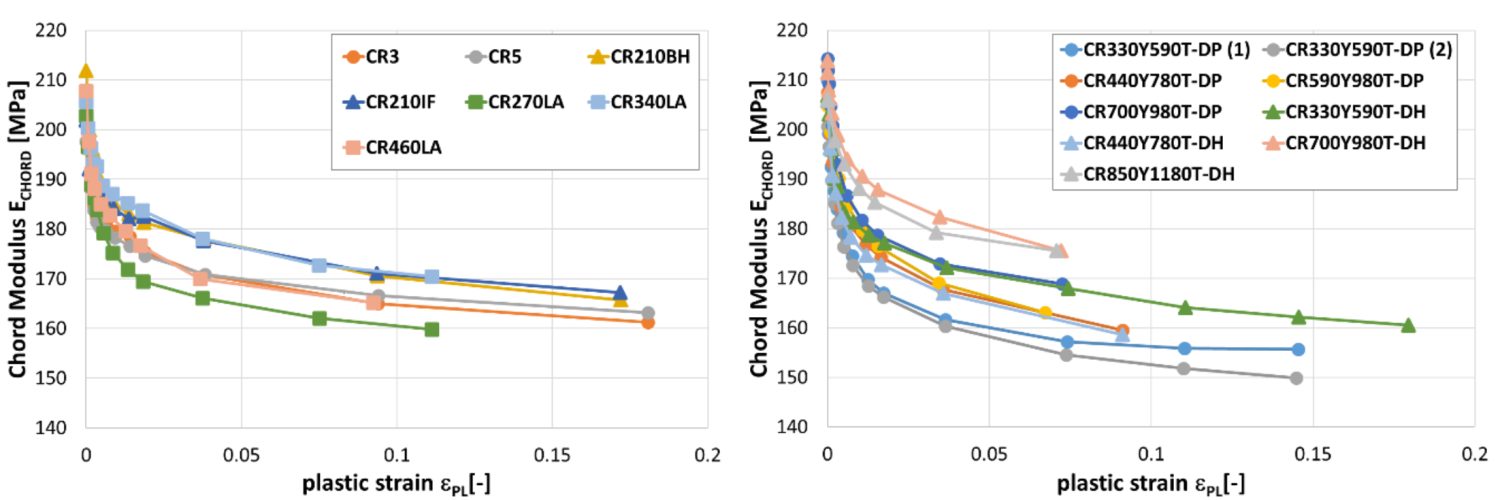
Reduction in chord modulus for mild steels and conventional high strength steels (left) and for DP and DH steels (right).W-10
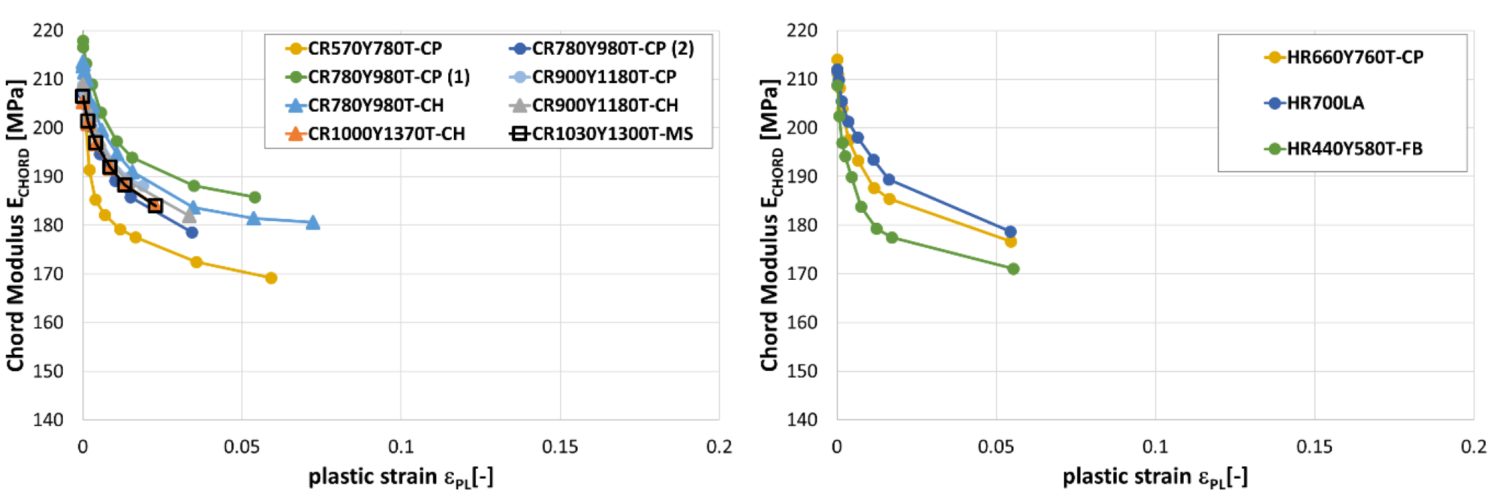
Reduction in chord modulus for CP, CH and MS steels (left) and for a selected of hot rolled steels (right).W-10








