Testing and Characterization
Many demands are placed on automotive body structures which influence the material selection process. The impact on safety, manufacturability, and longevity are among the most critical, with each of these balanced against cost and environmental concerns.
Formed sheet metal products experience a complex series of deforming, cutting, and joining before being placed in a body structure, where these components will be subjected to complex loading conditions during the product life cycle. Understanding the failure limits and the conditions which produce failure allows for the design of body structures which can withstand these demands.
Testing helps determine whether a metal is suitable for its intended use. Different tests characterize specific performance aspects. Historically, manufacturers relied on tensile testing to understand metal flow. However, new tests help us understand the behavior of new steel grades and their interactions more thoroughly with new manufacturing technologies.
![Tensile Testing]()
Testing and Characterization
topofpage
Tensile testing characterizes the forming and structural behavior of sheet metals. The test involves loading a sample with a well-defined shape along the axis in tension, generally to fracture, and recording the resultant load and displacement to calculate several mechanical properties. Global standardsI-7, A-24, D-19, J-15 prescribe the conditions under which tests must occur.
Sample Size and Shape
Full-size samples for tensile testing of metal sheets have a rectangular section at the edges for gripping by the test machine. Reducing the width in the central area promotes fracture in the monitored region. These geometrical features result in a sample shape which resembles a dogbone, leading to a descriptive term applied to test samples.
Dimensions of the dogbone samples are associated with tensile test standard from which they apply. ISO I, II, and III (described in Citation I-7) corresponds to the ASTMA-24, DIND-19, and JISJ-15 shapes, respectively. Figure 1 shows the dogbone shapes, highlighting the critical dimensions of width and gauge length. Refer to the Test Standards for other dimensions, tolerances, and other requirements.

Figure 1: Full-size tensile sample shapes for ISO I (ASTM), ISO II (DIN), and ISO III (JIS) standards.I-7, A-24, D-19, J-15
Significant differences exist in the width and gauge length of these tensile bar shapes. Although the ASTM and JIS bars have similar gauge length, the width of the JIS bar is twice that the ASTM bar. The ASTM and DIN bars have a 4:1 ratio of gauge length to width, where the JIS bar has a 2:1 ratio.
These shape differences mean that the calculated elongation changes depending on the test-sample standard used, even when testing identical material. With the combination of the shortest gauge length and widest sample, elongation from JIS bars typically are higher than what would be generated from the other shapes.
Yield strength and tensile strength are not a function of the shape of the tensile bar. Strength is defined as the load divided by the cross-sectional area. Even though each of the bars specify a different sample width (and therefore different cross-section), the load is normalized by this value, which negates differences from sample shape.
Shearing or punching during sample preparation may work-harden the edges of the tensile bar, which may lead to generating an inaccurate representation of the mechanical properties of the sheet metal. Test Standards require subsequent machining or other methods to remove edge damage created during sample preparation. Milling or grinding the dogbone samples minimizes the effects sample preparation may have on the results.
Tensile Test Procedure
The gauge length is the reference length used in the elongation calculations. Depending on the test standard, the gauge length is either 2 inches, 80 mm, or 50 mm. Multiplying the width and thickness within the gauge length determines the initial cross-sectional area before testing.
Grips tightly clamp the edges of the sample at opposite ends. As the test progresses, the grips move away from each other at a prescribed rate or in response to the restraining load. A load cell within the grips or load frame monitors force. An extensometer tracks displacement within the gauge length. Samples are typically tested until fracture.
During the tensile test, the sample width and thickness shrink as the length of the test sample increases. However, these dimensional changes are not considered in determining the engineering stress, which is determined by dividing the load at any time during the test by the starting cross-sectional area. Engineering strain is the increase in length within the gauge length relative to the starting gauge length. (Incorporating the dimensional changes occurring during testing requires calculating true stress and strain. The differences between engineering and true stress/strain are covered elsewhere (hyperlink to 2.3.2.1-Engineering/True)
A graph showing stress on the vertical axis and strain on the horizontal axis is the familiar engineering stress-strain curve, Figure 2. From the stress-strain curve, numerous parameters important for sheet metal forming appear, including:

Figure 2: Engineering stress-strain curve from which mechanical properties are derived.
Influence of Test Speed
Conventional tensile testing is done at strain rates slow enough to be called “quasi-static.” These rates are several orders of magnitude slower than the deformation rates during stamping, which itself is several orders of magnitude slower than what is experienced during a crash event.
Stress-strain curves change with test speed, typically getting stronger as the speed increases. The magnitude of these changes varies with grade. Significant challenges exist when attempting to characterize the tensile response at higher strain rates. Improved equipment and data collection capabilities are among the required upgrades.
Influence of Tensile Test Equipment
Advanced High-Strength Steels (AHSS) may challenge older test equipment. The load and displacement response must reflect only the contributions of the sheet metal, and not be influenced by the load frame and other testing equipment. In much the same way that insufficiently stiff press crowns deflect when stamping AHSS parts, tensile test load frames may similarly deflect, resulting in inaccuracies in the load-displacement measurements.
Grip strength also becomes critical when testing AHSS samples. The high strength of the metal sheets requires more grip pressure to prevent sample slippage through the grips. Pneumatic grips and even some mechanical grips may not generate the necessary pressure. Hydraulically actuated grips may be necessary as the strength increases.
Back to the Top
![Tensile Testing]()
Friction, Testing and Characterization
Friction is a restraining force that limits metal flow resulting from contact with another surface during sheet forming. Friction is influenced by the complex interaction between the sheet steel, lubricant, and tooling material, as well as many parameters of the forming system, some of which are shown in Figure 1.

Figure 1: Friction is influenced by the complex interaction between the sheet steel, lubricant, and tooling material, as well as many parameters of the forming system. (image modified from Citation K-13)
Friction changes throughout the stamping process as well as across the part, since there are changes in contact pressure, contact temperature, geometry, the sheet steel strength (work hardening), and even the sheet metal surface due to flattening of the peaks after flowing over beads and radii. There is no one friction value that applies to all geometries and forming scenarios that can be encountered.
Characterizing friction in a simulative test is similarly challenging, since there is no one simulative test that approximates all regions of an engineered stamping. For many years, tooling, design, and simulation engineers used one friction value for each galvanized coating / lubricant combination, and applied that value across every part stamped from that metal with that lubricant. The industry has evolved to using different tests to generate friction values appropriate for different forming conditions.
Simulative tests to characterize friction include test to reflect bending under tension, pulling through draw beads, and movement over flat surfaces. Depending on the test, it may be possible to evaluate the effect of tooling material, temperature, radii, and speed in order to better simulate production conditions. Figure 2 indicates which of these simulative tests apply to the regions of an in-process stamping. The value obtained in one test is a function of only those specific test conditions and should not be compared against values obtained in other tests.
- Bending Under Tension test: In the Bend Under Tension (BUT) test, a metal strip is drawn over a fixed cylindrical pin with a pair of independently controlled hydraulic actuators offset by 90 degrees. Two load cells measure the pulling force and back tension force. (Figure 3)
- Draw Bead test: Two sets of tests are done using a Draw Bead Simulator (DBS). In the first test, the force to pull sheet steel through a set of fixed draw beads is measured and reflects both the bending and unbending forces as well as the friction forces. Another sample is pulled through frictionless roller beads in a similar arrangement. Here, only the bending/unbending forces are active. Subtracting the results allows for determination of the forces due solely to friction. (Figure 4)
- Strip Draw: In the Strip Draw test, friction is determined by pulling sheet steel through opposing flat platens. The restraining condition is controlled by the force applied on the flat platens. The influence of bending is not considered in this test. (Figure 5)
Other tests are also used to provide some assessment of formability. Dome Testing simulates stretch forming conditions and can provide a relative comparison between different materials and lubricants. The Twist Compression Test (TCT) is used to compare the performance of different lubricants under controlled, repeatable conditions. Lubricant breakdown, which results in adhesion between the tool and the sheet steel, can be evaluated in the TCT.

Figure 2: Pertinent Simulative Tests During Stamping (image modified from Citation S-42)

Figure 3: The Bending Under Tension Test (image modified from Citation S-42)
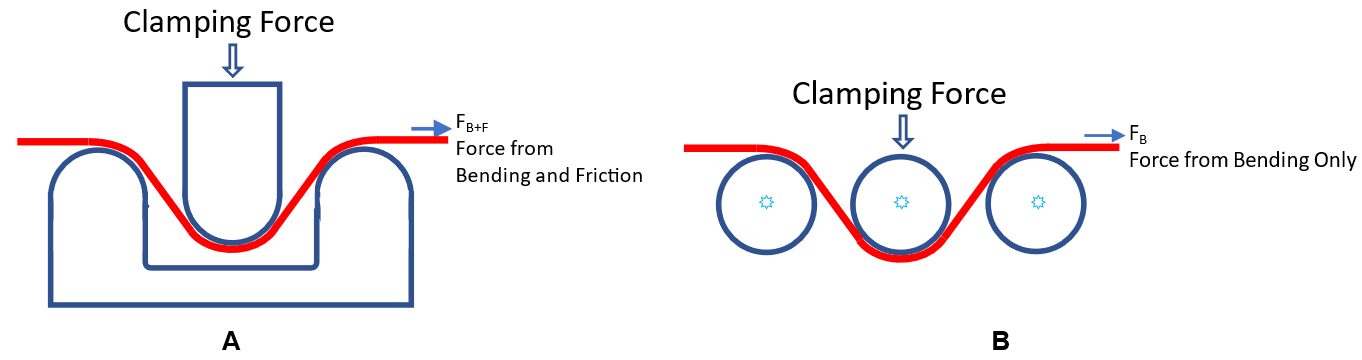
Figure 4: Draw Bead Simulator Testing determines the effect of friction from the differences in pulling force in two test conditions.
a) The strip pulled through fixed draw beads experiences restraining forces due to bending/unbending as well as forces due to friction.
b) The strip pulled through frictionless roller beads experiences restraining forces due only to bending/unbending.

Figure 5: The Strip Draw Test (image modified from U-6)
![Tensile Testing]()
Testing and Characterization
Local necking during uniaxial tensile testing limits the characterization of the stress-strain response to true strain values below uniform elongation. Extrapolating the true stress – true strain curve beyond uniform elongation requires selecting a hardening law on which to base the extrapolation. However, the chosen hardening law dramatically affects the extrapolated the true stress – true strain curve. Figure 1L-20 shows an example of this extrapolation using a bake hardenable steel. Deviation from the real performance leads to inaccurate thinning and fracture predictions, inaccurate springback predictions, and inaccurate predictions of press force and press energy requirements.

Figure 1: The selected hardening law leads to vastly different stress-strain responses extrapolated beyond uniform elongation.L-20
Bulge testing is one method to generate stress-strain data at higher strains, minimizing the need for extensive extrapolation. Another benefit is that the deformation occurs in two directions (biaxial), which is similar to the metal motion seen in most forming operations and in contrast to uniaxial tensile testing.
In biaxial bulge testingK-17, V-7, a circular sample is clamped around its periphery and pressurized from one side using a viscous incompressible medium, forcing the metal to bulge and expand into a cavity as the pressure increases. Figure 2 shows a typical testing configuration.F-12 Flow stress is calculated from the dome height of the bulging blank and the pressure in the viscous medium. A non-contact system equipped with Digital Image Correlation (DIC) measures strain. The ISO 16808 Test Standard details the requirements.I-12

Figure 2: Bulge testing configuration.F-12
For various reasons, flow stress data at the lowest strains are not as accurate as what is generated at higher strains. This leads to practitioners combining curves, using tensile data at low strains through uniform elongation, and bulge data after that. These blended curves result in a thorough true stress – true strain characterization over a wide range of strains, making it applicable to a variety of formed parts. Figure 3 shows a blended curve for the same alloy highlighted in Figure 1.

Figure 3: Flow curves for a bake hardenable steel generated by combining tensile testing with bulge testing.L-20
Biaxial bulge testing provides two critical inputs for advanced material characterizations required for simulation: biaxial anisotropy and biaxial yield stress.
