Fracture Toughness Characterization using the Essential Work of Fracture Method

Fracture Toughness Characterization using the Essential Work of Fracture Method

The complex shapes of automotive stampings lead to die designs and processing that may challenge the inherent formability of the selected sheet metal grade. 

Traditional grades, especially those of lower strength, fail from insufficient necking resistance for the chosen application.  Characterization of the resistance to necking instability, sometimes referred to as global formability, is done with the strain hardening exponent (n-value), true uniform strain, and the Forming Limit Curve.  Since these parameters can be mathematically described, forming simulation packages can accurately estimate the risk of necking and subsequent splitting.

Contrast this with newer grades where the sheet metal may still fail from insufficient necking resistance, but may also fail from fracture initiating at cut edges or tight bends.  This fracture-limited formability, sometimes called local formability, can be influenced by many parameters – including both inherent material characteristics as well as the processing conditions used to create the cut edge (hole diameter, clearance, punch geometry, and so on) or bend (inside bend radius divided by the thickness, r/t).  The inherent material characteristics contributing to this failure mode are not directly related to strength and elongation determined from traditional uniaxial tensile testing. Forming simulation packages have challenges estimating the risk of fracture-limited formability, since the full mathematical representation of the contributing factors does not yet exist.

To date, hole expansion testing is the most common way to characterize the edge stretchability of a particular sheet metal.  The typical test procedure, prescribed by ISO 16630, requires a 10 mm diameter hole punched with a 12% clearance to be expanded with a conical punch having a 60° apex angle.  Unfortunately, changing the testing conditions like the hole diameter, clearance, punch shape, or crack detection method has a significant influence on the results, to the point that any relative performance ranking of different products can change between the defined laboratory test conditions and the real-world performance.

Local fracture strain measurements from uniaxial tensile specimens, like true fracture strain, true thickness strain, or the reduction of the cross-section area at fracture, are also used to quantify fracture performance, and may offer better guidance for crash performance prediction.L-21, L-69   The bending angle measured from 3-point bending test according to VDA 238-100 or the fracture strain in plane strain tension obtained from these tests, are also effective in predicting bending-dominated failure that occurs with AHSS grades during folding/bending in axial and side crash tests. The bending angle and fracture strain determined in a 3-point bend test conducted according to VDA 238-100 correlates with the folding and bending seen in vehicle crash testing.  However, these parameters individually are not sufficient to characterize overall fracture behavior and therefore cannot be used as a singular failure criterion that is applicable to all situations.

 

Fracture Toughness

Fracture-limited formability is dependent on the sheet metal’s resistance to crack nucleation and propagation, which are the two parameters influencing fracture toughness.  As such, approaches have been investigated to experimentally assess the relationship between fracture toughness and cracking resistance of advanced steels.   

Conventional toughness estimations based on the product of tensile strength multiplied by the total elongation to fracture (TS * TEL) or the area under the stress-strain curve are not suitable to describe the fracture toughness of AHSS. Use of these shortcuts may lead to an incorrect fracture toughness ranking when considering multiple materials: consider the comparison of 980DP vs. 980CP. The dual phase steel has greater elongation to fracture and greater uniform elongation, yet the complex phase steel has better edge ductility and fracture toughness.  Tensile fracture parameters, such as the true fracture strain (εf) or the product of fracture stress and true fracture strain (σf × εf), give a better estimation of toughness at cracking initiation. However, these approaches can underestimate the crack propagation resistance of the material. To avoid misleading conclusions about the cracking resistance of high strength sheet metals, fracture toughness must be measured within the framework of fracture mechanics.F-43

Fracture toughness is defined as the energy spent in the creation of two surfaces at the crack tip that leads to crack propagation.  Traditional approaches to study fracture toughness include J-integral and Crack Tip Opening Displacement (CTOD) measurements, but these evaluations do not apply to thin-gauge materials such as those used in automotive body construction.  Alternative approaches appropriate for sheets below 3 mm thickness are relatively complex, involve detailed specimen preparation, and require measurement of the advancing crack during the tests.

 

Essential Work of Fracture Methodology

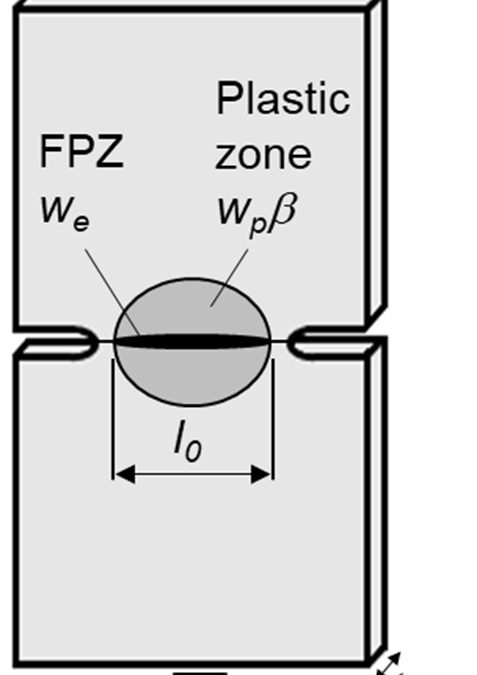
To address these challenges, a methodology based on the Essential Work of Fracture (EWF) appears to offer a simpler solution for measuring the fracture toughness of thin metal sheets.  The method described below has been validated in industrial applications using both steel and non-steel sheet metals. The Double Edge Notched Tensile (DENT) specimen is used for this characterization (Figure 1).  Since only tensile transverse stresses exist between the notches, and the geometry avoids the risk of buckling.

 
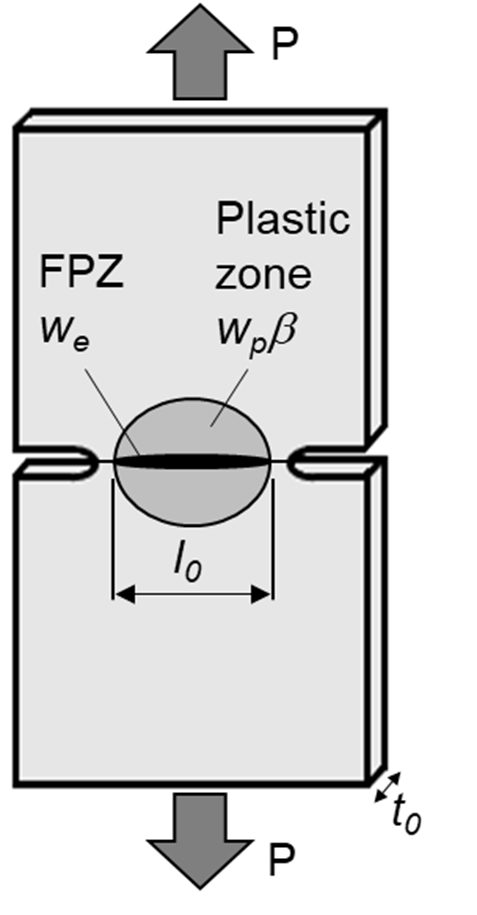
Figure 1: The Double Edge Notched Tensile (DENT) specimen is used for Essential Work of Fracture characterization.

Figure 1: The Double Edge Notched Tensile (DENT) specimen is used for Essential Work of Fracture characterization.

 

In the DENT specimen, all of the deformation takes place in and around the notched ligament, allowing for separation of the total fracture energy, Wf, into its two components:

a) We, the essential work of fracture that is related to damage and the work to create new surfaces in front of the progressing crack tip. This value is proportional to the fractured area.
b) Wp, the plastic work dissipated in the region surrounding the crack tip as a consequence of plastic deformation. This value is proportional to the deformed volume, which is a function of the sample size, geometry, and loading mode.

Mathematically, the total fracture energy may be represented by:

Wf = We + Wp                           Equation 1

These parameters can be further characterized.

We = we*l0*t0, where we is the essential work of fracture per unit area, l0 is the ligament length between the two notches, and t0 is the specimen thickness.

Wp = β*wp* l02*t0, where wp is the plastic work per unit volume and β is a shape factor that is a function of the shape of the plastic zone.

Substituting these into Equation 1 gives

Wf = we*l0*t0 + β*wp* l02*t0                                    Equation 2

Normalizing each side of Equation 2 by the fractured area l0*t0 produces wf, the fracture energy per fracture area:

Wf/ l0*t0 = wf = we + β*wp* l0                                  Equation 3

This procedure enables the separation of the specific essential work of fracture, we , and the non-essential plastic work, wp, from the total energy of fracture by using a simple data reduction method. A series of specimens with different ligament lengths are tested to fracture. The fracture energy per fracture area, wf, is then calculated by integrating the area under the load-displacement curve and normalizing by the cross-section area (wf= Wf /l0*t0) . . By plotting the series of wf values as a function of ligament length l0 as shown in Figure 2, then we and β*wp can be obtained by linear regression with we being the vertical axis intercept of a line with slope β*wp. It is relevant to keep in mind that this method to obtain we is a purely mathematic procedure to remove the non-essential plastic contribution to the fracture energy, i.e. it does not mean that we is the value of wf at zero ligament length. To guarantee data linearity and the validity of the energy partitioning concept, different validity criteria must be met.T-49  

The parameter we is a thickness-dependent material constant representing the plane stress fracture toughness of the material. Since it is obtained from a dataset of energy values for the complete fracture, it contains energetic contributions from both crack initiation and propagation resistance.

For each of the specimens tested with different ligament length, the work of fracture at crack initiation (wfi) is obtained from integrating the area under the load-displacement curve up to the point of crack growth initiation. This point has to be experimentally verified and generally it is around the peak values of the forces versus displacement curve. Since wfi is independent of the ligament length, the specific essential work for fracture initiation, wei can be calculated from an average of wfi values. This is also shown in Figure 2.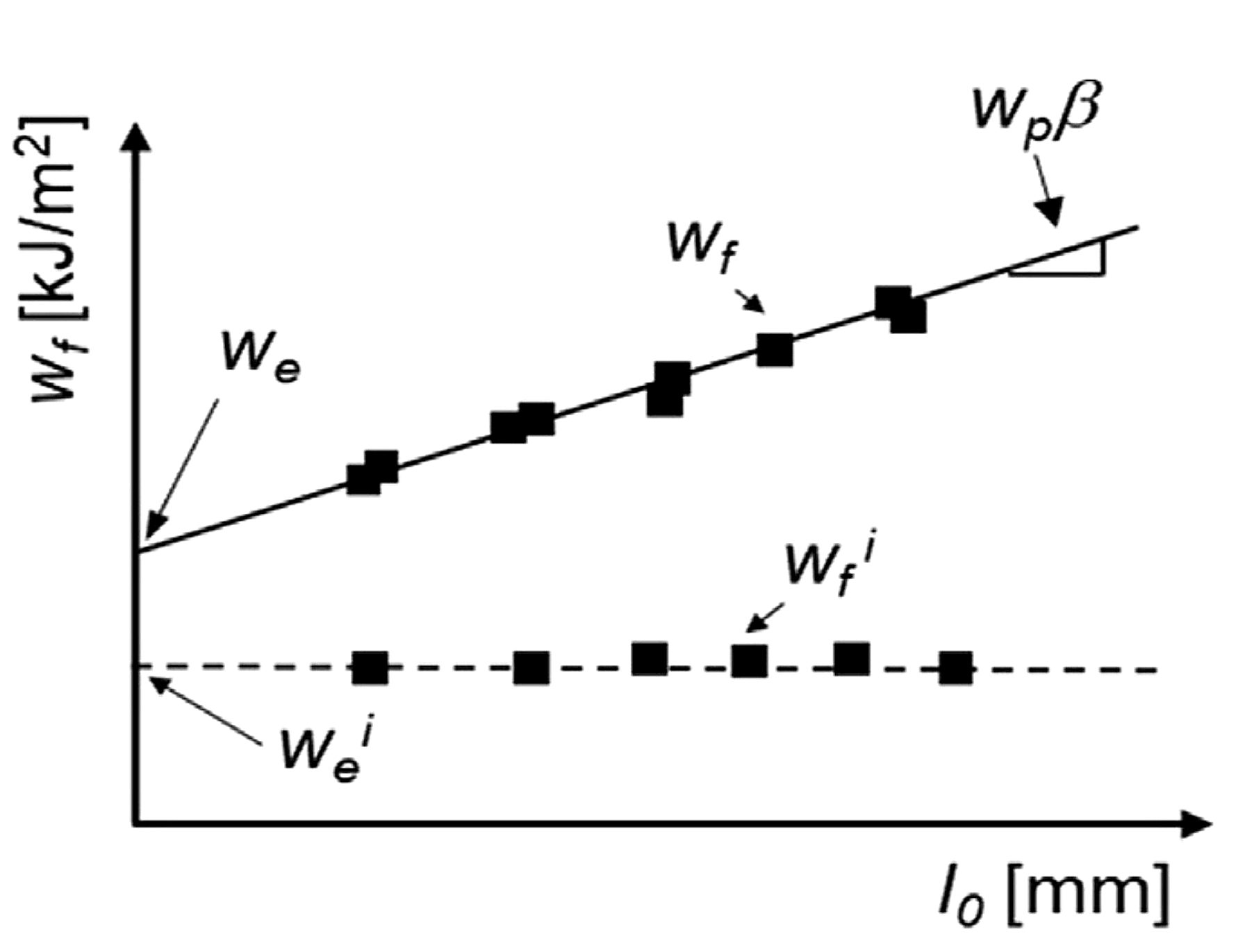Figure 2: The specific essential work of fracture, we, is the vertical axis intercept in the plot showing the relationship between the specific total work of fracture, wf, and the ligament length. The specific essential work of fracture initiation, wei, is the average of the values of the specific work of fracture at initiation of propagation, wfi.
Figure 2: The specific essential work of fracture, we, is the vertical axis intercept in the plot showing the relationship between the specific total work of fracture, wf, and the ligament length. The specific essential work of fracture initiation, wei, is the average of the values of the specific work of fracture at initiation of propagation, wfi. 

 

Figure 3 shows the specific essential work for fracture (we) and specific essential work for fracture initiation (wei) for several advanced high strength steels. The differences between these parameters vary between the grades.  For some grades, the markers fall nearly on top of each other, and for these, there is only a small contribution from crack propagation resistance once the crack initiates.  For other grades, including complex phase steels and the enhanced-ductility PHS grade, the crack propagation resistance is a significant portion of the overall fracture toughness.

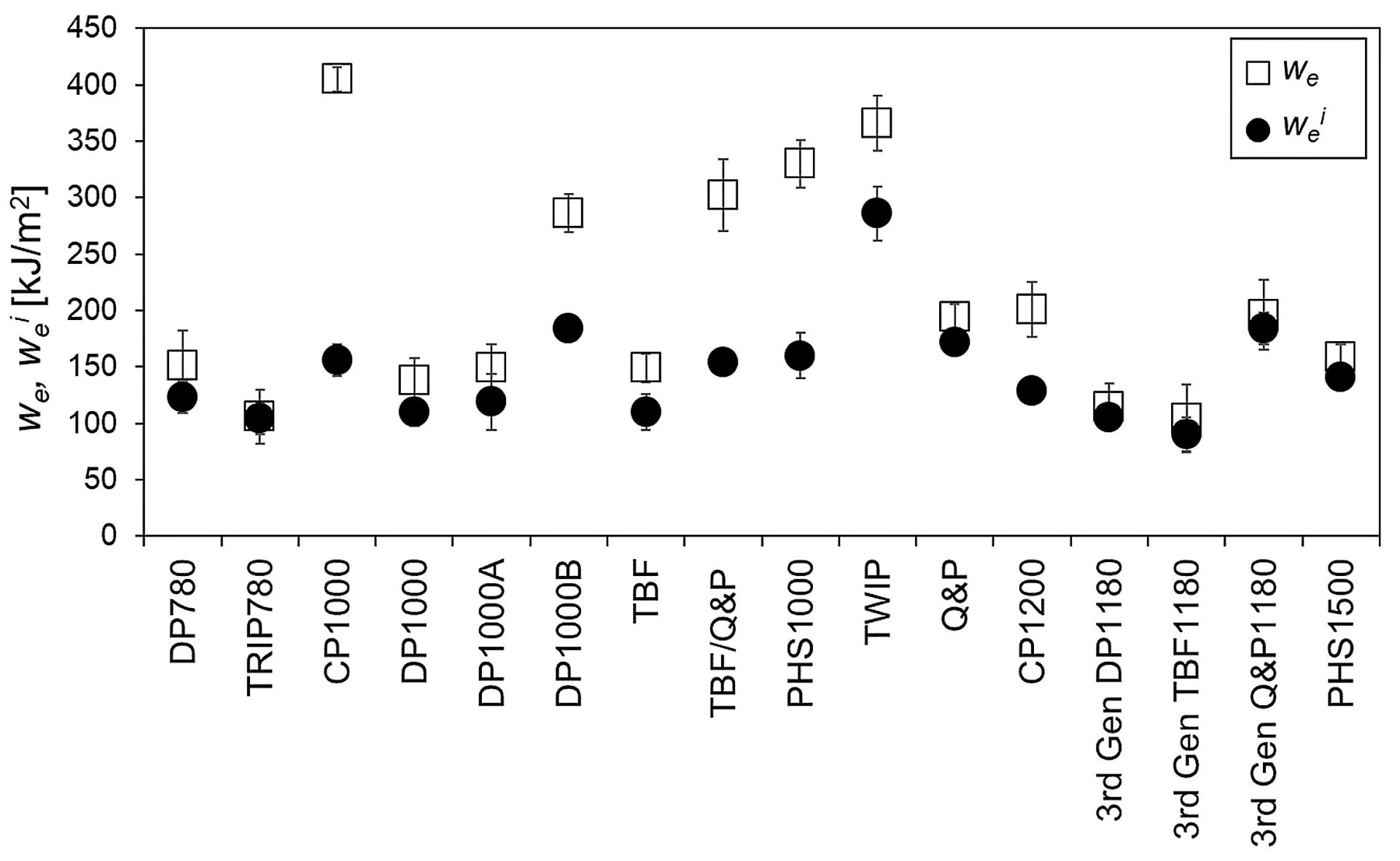
Figure 3: we and wei for several advanced high strength steels. F-44

Figure 3: we and wei for several advanced high strength steels. F-44

 

Notch root radius has a significant influence on EWF measurements. To obtain accurate and reliable fracture toughness values pre-cracked samples must be used. Alternative methods,  including fatigue pre-cracking, notch sharpening by a razor blade or mechanical sharp notching with a specific tool,  may be used for that purpose. ASTM E399 lists a procedure to nucleate a fatigue crack at the notch rootA-81, as does ASTM E1820A-82. These approaches are relatively costly and time consuming.  To address these concerns, a device consisting of a two-pillar modular cutting die and beveled punch was developed to shear sheet specimens in such a manner to introduce crack-like sharp notches.F-45, E-15  Without these efforts to generate an exceedingly small notch radius, the measured toughness values can overestimate the real crack initiation and propagation resistance of the material.F-43

Following the definition of the specific essential work of fracture we , the resistance to crack propagation, it is the material property to address crack-related problems in sheet metal forming, as edge cracking, or to account for part performance when cracks are involved, as in crash resistance tests. In this regard, there is good experimental correlation between the  we and the hole expansion ratio for a wide range of AHSS families, as shown in Figure 4.  As discussed above, although similarities exist in the fracture mechanisms involved in both tests, the hole expansion ratio is not a material parameter since it depends on several experimental factors such as the hole geometry, edge preparation method, and crack detection method. These choices lead to increased variability of results generated at different labs.  Aside from thickness, we is a material property that represents more accurately the sheet steel’s crack propagation resistance. Based on experimental observations a value of we larger than 250 kJ/m2 would be recommended when edge cracking may appear in sheet forming. On the contrary, values lower than 125 kJ/m2 may jeopardize the stamping process.

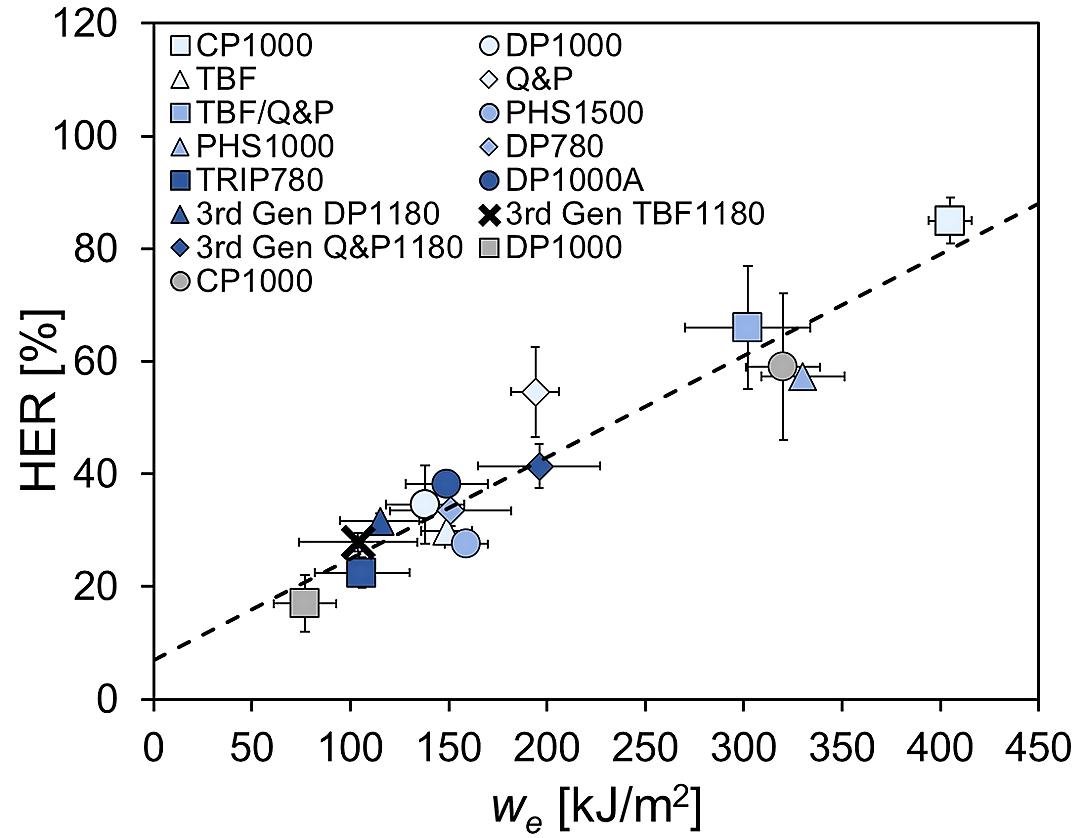
Figure 4: Correlation between we and hole expansion ratio (HER), based on data in references Citation F-44, F-46

Figure 4: Correlation between we and hole expansion ratio (HER), based on data in Citations F-44, F-46

 

Crash resistance can be also assessed through the values of the we. In AHSS the appearance of cracks during crash tests ranks crash resistance, so high cracking resistance steel leads to high crashworthiness. The energy absorbed by a component linearly increases with the specific essential work of fracture of the steel used to form the component (Figure 5), making we a good candidate to provide useful information in assessing crashworthiness.F-47

 

Figure 5a. Crash box made from DP1000 has limited energy absorbed before fracture. Citation F-44

Figure 5a. Crash box made from DP1000 can absorb only limited energy before fracture. F-44 

Figure 5b. Crash box made from CP1000 can absorb more energy before fracture. Citation F-44

Figure 5b. Crash box made from CP1000 can absorb more energy before fracture.F-44 

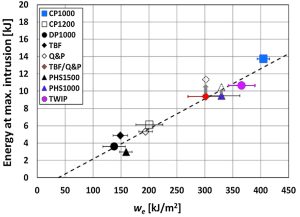Figure 5c. Energy absorbed at maximum intrusion as a function of the specific essential work of fracture for several advanced steels. Citation F-47

Figure 5c. Energy absorbed at maximum intrusion as a function of the specific essential work of fracture for several advanced steels.F-47 

 

Local Formability Diagrams such as the ones shown in Figures 3 and 4 of the Defining Steels page give the user an indication of how a chosen grade might perform in applications requiring fracture resistance, such as those inducing expansion of cut edges during forming.  Knowledge of the Essential Work of Fracture offers another representation, as reproduced in Figure 6.F-46   Figure 7 shows a similar representation having tensile strength on the horizontal axis, which is the same format as the conventional Global Formability Diagram.F-48

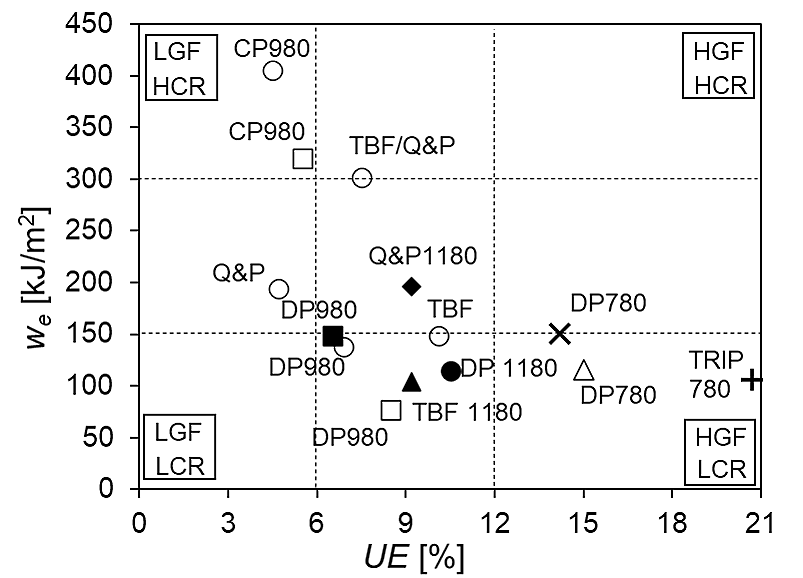
Figure 6: AHSS classification based on uniform elongation (UE, as an indicator of global formability) and fracture resistance (we). LGF low global formability, LCR low cracking resistance, HGF high global formability, HCR high cracking resistance. Citation F-46

Figure 6: AHSS classification based on uniform elongation (UE, as an indicator of global formability) and fracture resistance (we). LGF low global formability, LCR low cracking resistance, HGF high global formability, HCR high cracking resistance.F-46 

 

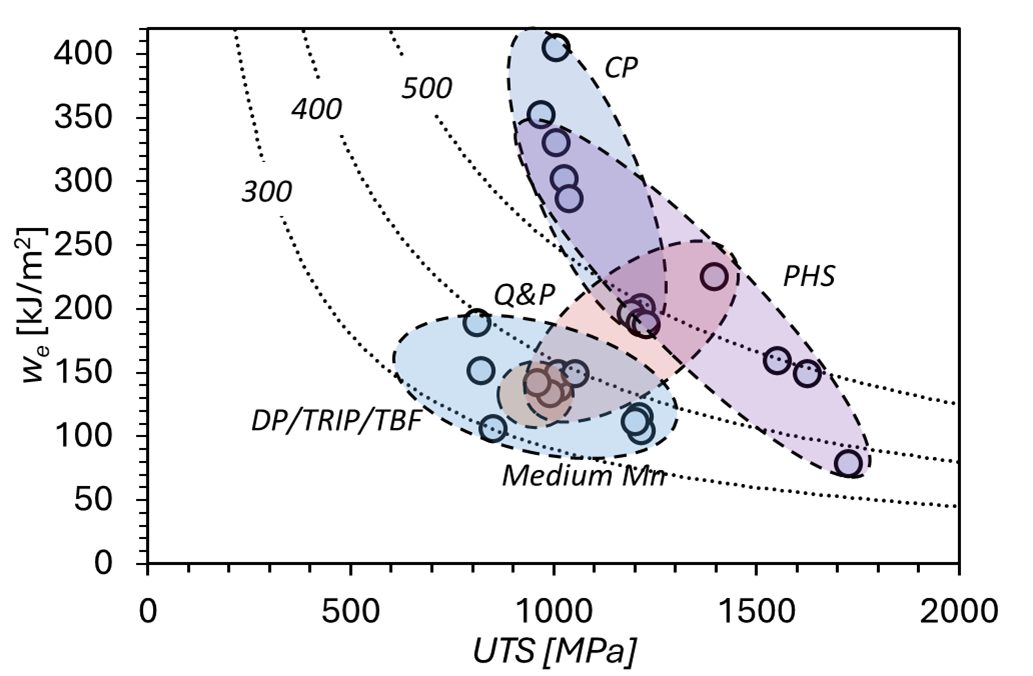
Figure 7: Fracture resistance (we) as a function of tensile strength (UTS) for several Advanced High Strength Steels. Citation F-48

Figure 7: Fracture resistance (we) as a function of tensile strength (UTS) for several Advanced High Strength Steels.F-48

 

Additional information about the Essential Work of Fracture methodology and its application in fracture toughness, cracking resistance, crashworthiness assessments, User Guidelines, and case studies can be found at https://toughsteel.eu/ as well as Citations C-37, C-38, and C-39.

Thanks are given to David Frómeta and Daniel Casellas of Eurecat for their assistance in preparing this page.

 

Bake Hardenable

Bake Hardenable

AHSS, Conventional HSS, Steel Grades

BH Grades

Bake Hardenable (BH) steels grades are conventional High Strength Steels that exhibit a Bake Hardening Effect. BH steels exhibit an increase in yield strength after room-temperature stamping followed by processing through a thermal cycle comparable to the time-temperature profile used in paint curing (or baking) – approximately 170 °C for 20 minutes. Bake hardenability is characterized by determining the Bake Hardening Index.

Bake Hardenable steel grades have yield strength at shipment from the steel mills of 180 MPa to 300 MPa (approximately 25 ksi to 45 ksi). The grades at the lower strength levels are capable of being produced with a Class A surface finish and are used in applications where dent resistance is desired in thin sheet steel. Applications for the higher strength BH steels include structural parts where Class A surface is not required. The higher strength after forming and baking is the reason automakers might use these in body structure applications, potentially contributing to vehicle lightweighting efforts.

These grades work harden approximately 30 MPa when 2% strain is introduced, either from stamping or during a tensile test, which is similar to dent resistant IF-HS. In contrast to IF-HS, the paint-bake cycle after forming results in an additional yield strength increase. The minimum strength increase from baking is specified by some automakers as 20 MPa to 35 MPa, measured after applying a defined level of strain.

Higher yield strength directly improves the dent performance. Even though BH grades and their non bake hardening counterpart IF-HS grades may have similar yield strength and thickness after forming, bake hardenable steels will show superior dent resistance due to the increase in yield strength from the paint baking operation.

Ferrite is the main microstructural phase of BH steels. The strengthening from the paint bake cycle is due to the controlled amount of carbon remaining in solid solution (on the order of 25 ppm) when the steel leaves the production mill. At the baking temperatures after the part is formed, the dissolved carbon migrates to pin any free dislocations created from stamping. This increases the yield strength of the formed part for increased dent resistance. Formability does not suffer, since the strength increase occurs after stamping.

Most Advanced High Strength Steel (AHSS) grades also exhibit a Bake Hardening Effect, achieving yield strength increases of 40 MPa to 120 MPa from an appropriate thermal cycle. AHSS grades are not categorized with traditional bake hardenable steels, since their primary characteristics and applications are typically, but not exclusively, different. One exception are some Dual Phase (DP) steels available with a Class A surface, which are used as skin panels to combine excellent dent resistance with lightweighting benefits.

Some of the specifications describing uncoated Bake Hardenable (BH) steel are included below, with the grades typically listed in order of increasing minimum yield strength and ductility. Different specifications may exist which describe uncoated or coated, or steels of different strengths.

  • ASTM A1008M, with the terms BHS 26 [180], BHS 31 [210], BHS 35 [240], BHS 41 [280], BHS 44 [300]A-25
  • EN10268, with the terms HC180B, HC220B, HC260B, and HC300LAD-3
  • JIS G3135, with the term SPFC340HJ-3
  • JFS A2001, with the terms JSC270H, JSC340HJ-23
  • VDA239-100, with the terms CR180BH, CR210BH, CR240BH, and CR270BHV-3

 

Bake Hardening Effect

Bake Hardenable Steel Grades and most AHSS grades exhibit a Bake Hardening Effect, meaning that there is an increase in yield strength after room-temperature stamping followed by processing through a thermal cycle comparable to the time-temperature profile used in paint curing (or baking) – approximately 170 °C for 20 minutes.

The degree to which a sample is bake hardenable is characterized by the Bake Hardening Index.

In Bake Hardenable Steel Grades, solid solution hardening elements like phosphorus, manganese, and silicon are used to achieve the desired initial strength. For AHSS, the initial strength is determined by the balance and volume fraction of microstructural components like ferrite, bainite, retained austenite, and martensite. In both cases, a specifically engineered amount of dissolved carbon in the ferritic matrix causes an additional increase in the yield strength through controlled carbon aging during the paint-bake thermal cycle. The bake hardening process in AHSS grades is more complex, and results in substantially higher values of the Bake Hardening Index.

Figure 1 shows the work hardening and bake hardening increases for samples of three High-Strength steel grades having the same as-received yield strength prior to 2% pre-straining and baking. The HSLA steel shows little or no bake hardening, while AHSS such as DP and Transformation Induced Plasticity (TRIP) steels show a large positive bake hardening index. The DP steel also has significantly higher work hardening than HSLA or TRIP steel because of higher strain hardening at low strains. No aging behavior of AHSS has been observed due to storage of as-received coils or blanks over a significant length of time at normal room temperatures. Hence, significant mechanical property changes of shipped AHSS products during normal storage conditions are unlikely.

The higher bake hardening index (BHI) of AHSS grades DP 600 and TRIP 700 is also shown in Figure 2. While BHI is determined at a prestrain of 2%, this graph indicates that even higher levels of bake hardenability can be achieved with increasing strain. In a stamping where most areas have more than 2% strain, combining this higher bake hardenability with the increased work hardening that occurs with increasing strain results in a formed panel having a strength markedly higher than the incoming flat steel. This is beneficial for crash energy management.

Figure 1: Comparison of work hardening (WH) and bake hardening (BH) for TRIP, DP, and HSLA steels given a 2% prestrain. S1, K3

Figure 1: Comparison of work hardening (WH) and bake hardening (BH) for TRIP, DP, and HSLA steels given a 2% prestrain. S-1, K-3

 

Figure 2: Bake hardening responses of several HSS and AHSS products with varying pre-strain, reproduced from Figure 3 in Citation B-6. The bracketed numbers after each grade are references within the cited paper.

Figure 2: Bake hardening responses of several HSS and AHSS products with varying pre-strain, reproduced from Figure 3 in Citation B-6. The bracketed numbers after each grade are references within the cited paper.

 

Bake Hardenability of Exposed Quality Dual Phase Steels

Dent resistance is a function of the yield strength in the formed panel after it completes the paint baking cycle. Based on this premise, grades with higher bake hardenability, such as AHSS, should have substantially higher dent resistance. Application of AHSS grades to capitalize on improved dent resistance also requires their production at the desired thickness and width along with surface characteristics appropriate for Class A exposed quality panels. Some DP steels meet these tight requirements specified by the automotive industry.

A recent studyK-49 highlights this improved dent resistance. This work presents the experimental results and associated numerical investigation of the dent testing of DP270Y490T, a DP steel grade with 490 MPa minimum tensile strength. Tests performed to the SAE J2575 procedureS-7 measure the resultant dent depth after testing, so therefore smaller depths indicate improved performance. Compared with samples not processed through a bake hardening cycle, dent depth reductions occur with hotter and longer cycles, as shown in Figure 3. Increasing temperature plays a more significant role in dent depth reduction than increasing time. This work also reinforces that bake hardenability must be incorporated into simulation models in order to improve the accuracy of dent resistance predictions.

Figure 3: Dent resistance of DP270Y490T according to SAE J2575S-7* as a function of baking test conditions.K-49  Lower dent depth indicates better dent resistance.

Figure 3: Dent resistance of DP270Y490T according to SAE J2575S-7 as a function of baking test conditions.K-49 Lower dent depth indicates better dent resistance.

 

Bake Hardenability of 980 MPa and 1400 MPa Multi-Phase Steels with Different Prestrains

Citation X-5 evaluated the bake hardenability as a function of pre-strain on two steels having a microstructure of ferrite and martensite. The two steels are distinguished by their tensile strength:  Test steel 1# is a 980 MPa grade with a yield:tensile ratio of 80%, whereas test steel 2# is a 1400 MPa grade with a yield:tensile ratio of 85%.  See Table 1 for details.

Steel
ID #		 Thickness
(mm)		 Yield Strength
(MPa)		 Tensile Strength
(MPa)		 Elongation
(%)		 Elongation at Break
(%)
1# 1.5 832 1047 7 13.5
2# 1.4 1243 1455 4 7
Table 1: Mechanical Properties of Tested Steels. X-5

 

Conventional uniaxial tensile testing of a #5 JIS bar was used to apply prestrain and evaluate mechanical properties. After pre-straining, samples were tested by first bending coupons to 90°, followed by the conventional paint bake thermal cycle of 170 °C for 20 minutes except for the control samples which remained unbaked. In all cases, the bend line was parallel to the rolling direction.

In the absence of prestrain, no bake hardening was observed in the two steels, indicating that prestrain is a prerequisite for promoting bake hardening.

Increasing levels of prestrain did increase the bake hardening response, but only to a certain level, with the two steels having a different prestrain response. The lower strength Steel 1# reaches a maximum BH value of approximately 80 MPa at a prestrain of 2%, while the higher strength Steel 2# reaches a maximum BH value of approximately 160 MPa at a prestrain of 1%. See Figure 4.

Figure 4: Effect of prestrain on Bake Hardening of 980 MPa and 1400 MPa steels. X-5

Figure 4: Effect of prestrain on Bake Hardening of 980 MPa and 1400 MPa steels.X-5

 

The elongation to fracture response to increasing prestrain is found in Figure 5, which shows a continuous decrease in ductility.

Figure 5: Effect of prestrain on Elongation of 980 MPa and 1400 MPa steels. X-5

Figure 5: Effect of prestrain on Elongation of 980 MPa and 1400 MPa steels.X-5

 

Using these grades in production applications requires the formed product to be capable of withstanding additional damage if involved in a crash.  As such, some coupons bent to 90° were baked while others remained unbaked, and all were subsequently bent another 30°, producing a final bending angle of 60°. 

Baking has an adverse effect on the secondary bending performance of the 1400 MPa grade, which required a bend radius of 3 mm to avoid bend cracks in the baked condition. Without baking, a 2 mm radius was successfully bent.  In the 980 MPa grade, no cracking was found even with a 1 mm radius in either the unbaked and baked conditions.

 

Measuring The Bake Hardenability Index

Bake hardenability is characterized by determining the Bake Hardening Index, or BHI.

The Bake Hardening Index (BH2) is determined by taking a conventional tensile test sample and pulling it to 2% strain. This is known as a 2% pre-strain. The sample is then put into an oven for a thermal cycle designed to be typical of an automotive paint curing (paint baking) cycle: 170 °C for 20 minutes. The temperature and time may be different depending on the end-user specifications.

Some companies may specify BH0, which uses the same thermal cycle without the 2% pre-strain. BH5 or BH10 (5% or 10% pre-strain, respectively) may also be reported.

The experimental procedure and calculation of BH2 is standardized in EN 10325D-4 and JIS G 3135J-3, and is similarly described in several other specifications.

Figure 6 defines the measurement for work hardening (B minus A), unloading to C for baking, and reloading to yielding at D for measurement of bake hardening (D minus B).  Note that the bake hardening index shown here is measured up to the lower yield point, which is consistent with the EN 10325 definition.  JIS G 3135 prescribes the use of the upper yield point.

Figure 4: Measurement of work hardening index and bake hardening index.

Figure 6: Measurement of work hardening index and bake hardening index.  BHI is measured using the lower yield point in EN 10325D-4 and with the upper yield point in JIS G 3135J-3.

 

Back To Top